真性半導体のキャリア密度とフェルミ準位
1.真性半導体とは
真性半導体
とは、全く不純物のはいっていない (とみなせる) 半導体のことである。現在使われている半導体の純度はとんでもない数字で、例えばSiなら純度99.9999999999999% (9が15個) とかそういうレベルのものだ。半導体の特性を調べるには、まずバンド構造を知らないといけない。SiやGe, GaAsといった有名どころの半導体材料では、X線で観測した結晶構造をもとに、結晶のシュレディンガー方程式がコンピュータによって解かれていて (第一原理計算)、電子のバンド構造がかなり良い精度で求まっている。(良い精度といったのは、実は電子のバンド構造を直接見に行ける実験があるのだ。ARPESと呼ばれる。) そしてそのバンド構造の大概は、フェルミ準位付近で以下のように放物線形になる。図の2つのバンドには名前がついていて、上の放物線によって表されているバンドを
伝導帯
、下の放物線のバンドを価電子帯
という。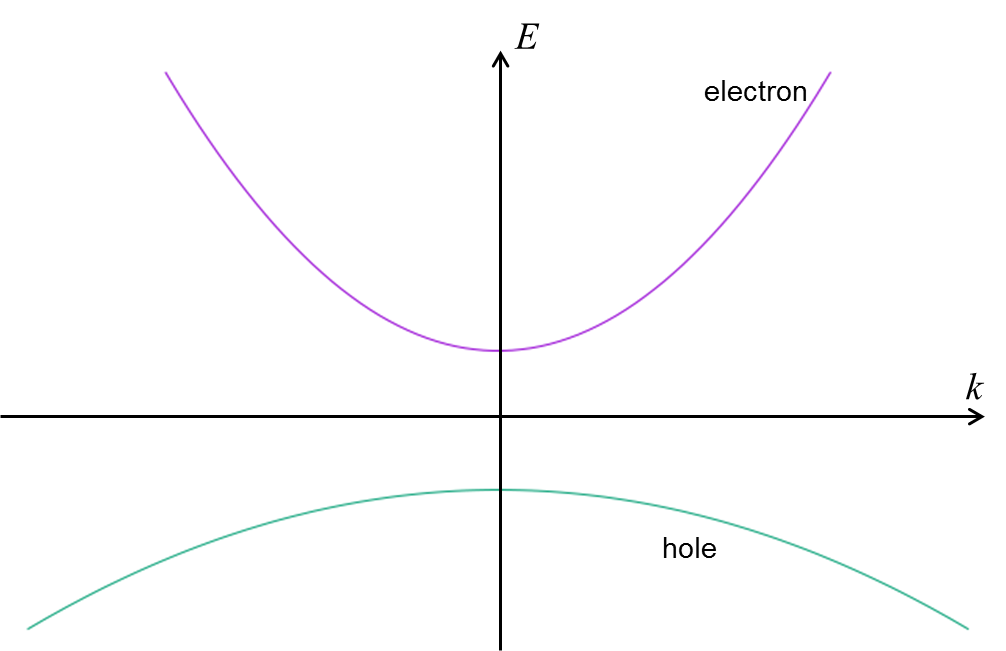
もしかしたら結果だけ知りたい人も多いかもしれないので、先に結果を書いておく。 \[n=\frac{1}{4}\left(\frac{2m^*_ekT}{\pi\hbar^2}\right)^{3/2}\exp\left(-\frac{E_c-\mu}{kT}\right)\] \[p=\frac{1}{4}\left(\frac{2m^*_hkT}{\pi\hbar^2}\right)^{3/2}\exp\left(\frac{E_v-\mu}{kT}\right)\] \[N_c = \frac{1}{4}\left(\frac{2m^*_ekT}{\pi\hbar^2}\right)^{3/2}\] \[N_v =\frac{1}{4}\left(\frac{2m^*_hkT}{\pi\hbar^2}\right)^{3/2}\] \[\mu =\frac{E_c+E_v}{2}+\frac{3}{4}kT\ln\frac{m^*_h}{m^*_e} \] \[n_i = \sqrt{N_cN_v}\exp\left(-\frac{E_g}{2kT}\right)\]
- \(n,p\): 伝導帯・価電子帯のキャリア密度
- \(m^*_e,m^*_h\): 伝導帯・価電子帯の有効質量
- \(E_c,E_v\): 伝導帯の底・価電子帯の頂上のエネルギー
- \(\mu\): フェルミ準位
- \(E_g\): エネルギーギャップの幅
- \(N_c,N_v\): 伝導帯・価電子帯の実効状態密度
- \(n_i\): 真性キャリア密度
2.フェルミ準位
まず勘違いしてはいけないのは、フェルミ準位は物質によって決まっている定数であるというよりも、その原子のもっている電子の数から決まるものだというところだ。フェルミ準位とは何なのかという記事でも書いた。ここのところを勘違いしていると正しい理解は得られない。そこでまずはフェルミ準位の一般論から確認しておこう。電子の状態密度を\(D(\epsilon)\)とし、そこにあるべき電子数を\(N\)、フェルミディラック分布関数を \[f(\epsilon) = \frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}\tag{1}\] とする。この\(\mu\)がフェルミ準位 (化学ポテンシャル) だ。\(\mu\)は、電子数\(N\)と温度\(T\)によって決まる変数であり、 \[N=\int f(\epsilon)D(\epsilon)d\epsilon\tag{2}\] を満たすようにしなければいけない。詳しくはフェルミ準位とは何なのかという記事を参照。
しかし、(2)では右辺の積分を全てのバンドに対して行わなければならず、結構難しい。原子間に共有されている電子だけではなく、各々の原子に束縛されているような電子まで考えなくてはいけないのだ。これでは定性的な理解すら得られそうにないだろう。そこで、この条件式(2)を次のように考えて簡単化してみよう。
真性半導体の場合、下の図のように必ず正孔と電子はペアで生成される。
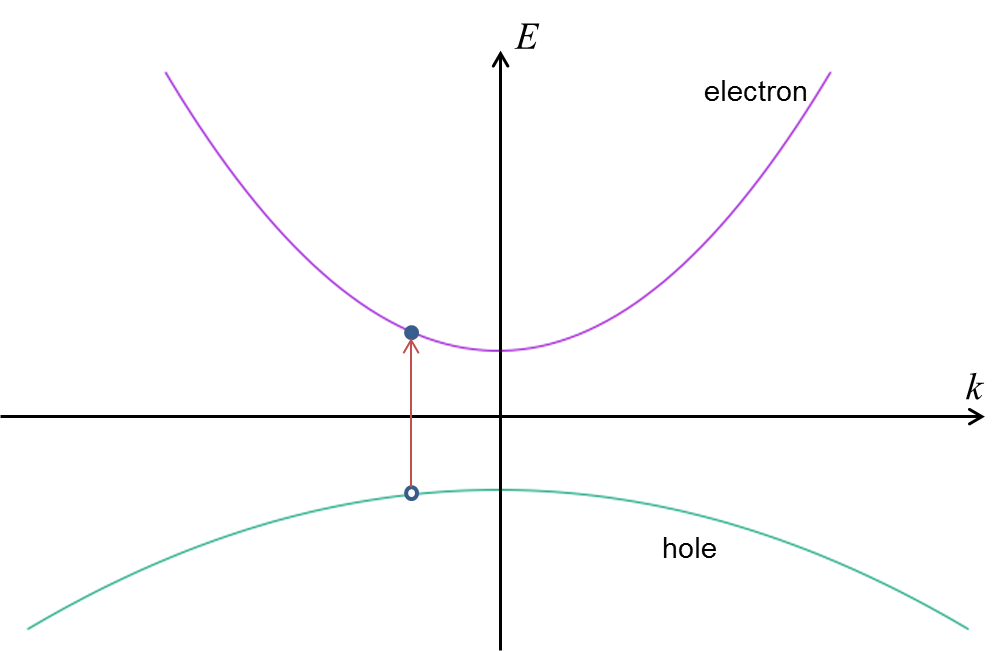
なぜこんな回りくどい仮定を入れたかというと、とても小さく、無視できるほどの確率ではあるのだが、かなり下の方の準位から励起されている電子や、もっと上の準位まで飛んでしまって電子だっているかもしれないからだ。
そこで、このことを使ってフェルミ準位を決める(2)を書き換えよう。少し考えると、この仮定のもとでは、全電子数が\(N\)になるということと、励起電子の数\(n\)と正孔の数\(p\)が等しいということが等価であるとわかるはずだ。だから、(2)式は \[n=p\tag{3}\] と同じことになる。この(3)を満たすようにフェルミ準位\(\mu\)が決まるのだ。
しかしまだ(3)には明示的に\(f(\epsilon)\)が出てきていないので、\(n,p\)が\(f(\epsilon)\)によってどのように表されるか示していこう。励起電子の数\(n\)は、伝導帯の状態密度\(D_n(\epsilon)\)を使って、 \[n=\int f(\epsilon)D_n(\epsilon)d\epsilon\tag{4}\] とできる。これは簡単だ。次に正孔の数\(p\)はどうなるかというと、正孔というのは電子がいない準位のことだから、その分布関数は\(1-f(\epsilon)\)になる。だから、価電子帯の状態密度を\(D_p(\epsilon)\)として \[p=\int (1-f(\epsilon))D_p(\epsilon)d\epsilon\tag{5}\] となる。この(4)と(5)を(3)に代入すれば、フェルミ準位が求まるわけだ。でも、具体的にその値を求めるには、(4)や(5)の積分をしないといけない。
3.キャリア密度の計算
まずは\(n\)から計算してみよう。\(n\)を求めるには、状態密度\(D_n\)を知る必要がある。状態密度がどのように決まっていたかというと、それはエネルギーバンド\(E(k)\)の形によって決まるのだった。デルタ関数の和としての状態密度のページが参考になるはず。さて、半導体のバンドがどのようになっているかというと、図で示したように、バンドの底は放物線状の形をしていて、\(E(k)\)は二次関数で十分近似できるようなものだ。だから、伝導帯の有効質量を\(m_e^*\)とすると、 \[E(k) = \frac{\hbar^2}{2m^*_e}k^2+E_c\tag{6}\] である。\(E_c\)は伝導帯の底のエネルギー。(有効質量の定義そのままである。)
(6)式は電子の質量が\(m^*_e\)になっただけで、他は全く自由電子のバンドと同じだ。だから、自由電子の状態密度のページで導出したとおり、(6)式のバンドにおける状態密度は、 \[D_n(E)=\frac{1}{2\pi^2}\left(\frac{2m^*_e}{\hbar^2}\right)^{3/2}\sqrt{E-E_c}\tag{7}\] である。これを(4)に代入する。ついでに\(f(\epsilon)\)も代入してやろう。すると、 \[n=\frac{1}{2\pi^2}\left(\frac{2m^*_e}{\hbar^2}\right)^{3/2}\int_{E_c}^{E_t} \frac{\sqrt{\epsilon-E_c}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\tag{8}\] ただし、積分範囲の上\(E_t\)は伝導帯電子に許される一番高いエネルギーである。さて、難しそうな積分が出てきた。この積分は
フェルミ積分
と呼ばれていて、簡単には計算できないものだ。本当なら数値計算に頼らないといけないのだが、半導体の場合は近似が使える。近似には、半導体の場合に\(E_c-\mu \gg kT\)が成り立っているという事実を使う。\(\mu\)というのは大雑把に言って、電子が素の状態 (熱エネルギーなしで) 入ることのできる準位のなかで一番高いエネルギーのことなのだから、\(E_c -\mu\)は電子が伝導帯に入るために獲得しないといけない熱エネルギーである。もしこれが\(kT\)と同じ程度であれば、伝導帯に電子が大量に入ってしまい、半導体というよりもむしろ金属的になってしまうだろう。だから、電流の流れにくい半導体については、\(E_c-\mu \gg kT\)が成り立っているといえるのだ。
そうすると、指数関数が\(1\)に比べてとても大きくなるから、フェルミ分布の分母の1を無視してしまって \[\frac{\sqrt{\epsilon-E_c}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)} \approx \sqrt{\epsilon-E_c}\exp\left(-\frac{\epsilon-\mu}{kT}\right)\tag{9}\] と近似できる。さらに、伝導帯の頂上のエネルギー\(E_t\)では、被積分関数はほとんど0になるだろうから、積分範囲の上限は\(\infty\)で置き換えてやろう。
この近似を入れてしまえばあとは簡単な計算だ。次のように進めていける。 \begin{align} n&\approx\frac{1}{2\pi^2}\left(\frac{2m^*_e}{\hbar^2}\right)^{3/2}\int_{E_c}^{E_t} \sqrt{\epsilon-E_c}\exp\left(-\frac{\epsilon-\mu}{kT}\right)d\epsilon\\ &=\frac{1}{2\pi^2}\left(\frac{2m^*_e}{\hbar^2}\right)^{3/2}\int_{0}^{\infty} \sqrt{s}\exp\left(-\frac{s+E_c-\mu}{kT}\right)ds~~~~(s=\epsilon-E_c)\\ &=\frac{1}{2\pi^2}\left(\frac{2m^*_e}{\hbar^2}\right)^{3/2}\exp\left(-\frac{E_c-\mu}{kT}\right)\int_{0}^{\infty} \sqrt{s}\exp\left(-\frac{s}{kT}\right)ds\\ &=\frac{1}{2\pi^2}\left(\frac{2m^*_ekT}{\hbar^2}\right)^{3/2}\exp\left(-\frac{E_c-\mu}{kT}\right)\int_{0}^{\infty} \sqrt{y}\exp\left(-y\right)dy~~~~(y=\frac{s}{kT})\\ &=\frac{1}{\pi^2}\left(\frac{2m^*_ekT}{\hbar^2}\right)^{3/2}\exp\left(-\frac{E_c-\mu}{kT}\right)\int_{0}^{\infty} x^2\exp\left(-x^2\right)dx~~~~(x=\sqrt{y})\\ \end{align} 積分を真面目に計算してもいいが、ここでは公式を使ってしまおう。 \[\int_{0}^{\infty} x^2\exp\left(-x^2\right)dx = \frac{\sqrt{\pi}}{4}\] を代入すると、 \[n\approx\frac{1}{4}\left(\frac{2m^*_ekT}{\pi\hbar^2}\right)^{3/2}\exp\left(-\frac{E_c-\mu}{kT}\right)\tag{10}\] となり、これで伝導帯電子の密度\(n\)が求まった。価電子帯にいるホールについても全く同じような計算をすれば、その密度 \(p\)が \[p\approx\frac{1}{4}\left(\frac{2m^*_hkT}{\pi\hbar^2}\right)^{3/2}\exp\left(\frac{E_v-\mu}{kT}\right)\tag{11}\] と得られる。\(E_v\)は価電子帯の頂上のエネルギーである。指数の前についている係数は、よく \begin{align} N_c &= \frac{1}{4}\left(\frac{2m^*_ekT}{\pi\hbar^2}\right)^{3/2}\tag{12}\\ N_v &= \frac{1}{4}\left(\frac{2m^*_hkT}{\pi\hbar^2}\right)^{3/2}\tag{13} \end{align} と書かれ、それぞれ伝導帯・価電子帯の
実効状態密度
と呼ばれている。実際には電子やホールはバンドに分布して色々なエネルギーを持つものがいるのだが、励起されている電子やホールの数に着目すると、「実効的」に伝導帯の底や価電子帯の頂上のエネルギー\(E_c,E_v\)とフェルミレベル\(\mu\)の差だけで決まっているように見えるのだ。さて、これでキャリア密度が求まったから、次はフェルミ準位を求めよう。