フェルミ分布・ボーズ分布の導出
1.量子力学的粒子
量子力学で取り扱われる粒子は、必ず2種類に分類することができる。フェルミ粒子とボーズ粒子だ。- フェルミ粒子: 粒子の入れ替えに関して波動関数の符号が反転するもの。同じ状態には一つの粒子しか入れない。
- ボーズ粒子: 粒子の入れ替えに関して波動関数の符号が変わらないもの。同じ状態に何個でも粒子が入ることができる。
2.フェルミ粒子の分布関数
フェルミ粒子の場合、あるエネルギー\(\epsilon\)をもつ一つの状態に入っている粒子の個数は必ず0個か1個である。ある一つの状態には一つの粒子しか入れないからだ。そこで、ここからはこの一つの状態だけに着目して、まわりに無限に存在するであろう状態は熱浴として取り扱う。熱浴には十分多くの粒子がいて、また温度\(T\)と化学ポテンシャル\(\mu\)を持っているとする。熱浴と言っているのだから、注目している状態とは平衡状態にある。熱浴となっている他の状態から、着目している状態に粒子が出たり入ったりしているような状況だ。
さて着目している状態に粒子が入っている確率を求めたい。分配関数は、次のように計算されるのだった。 \[Z=\sum_\b{N}\sum_\epsilon\exp\left(\frac{\b{N}\cdot\b{\mu}-\epsilon}{kT}\right)\tag{1}\] これがわかれば、着目している系があるエネルギー\(\epsilon_a\)・粒子数\(\b{N}_a\)をもつ状態\(a\)とる確率\(P(\epsilon_a)\)が、 \[P(\b{N}_a,\epsilon_a)=\frac{1}{Z}\exp\left(\frac{\b{N}_a\cdot\b{\mu}-\epsilon_a}{kT}\right)\tag{2}\] と計算できる。
今回は一種類の粒子を考えるから、 \[Z=\sum_N\sum_\epsilon\exp\left(\frac{N\mu-\epsilon}{kT}\right)\tag{3}\] となる。さらに、着目している状態には粒子が0個か1個しか許されておらず、0個入っているときにはエネルギーは0、1個入っているときにはエネルギーは\(\epsilon\)である。だから(3)の和は簡単に書き下せて、 \[Z=1+\exp\left(\frac{\mu-\epsilon}{kT}\right)\tag{4}\] となる。これから、粒子が入っていない確率は、 \[P_0 = \frac{\exp\left(\frac{0}{kT}\right)}{Z} = \frac{1}{1+\exp\left(\frac{\mu-\epsilon}{kT}\right)}\tag{5}\] であり、入っている確率は、 \[P_1 = \frac{\exp\left(\frac{\mu-\epsilon}{kT}\right)}{Z} = \frac{\exp\left(\frac{\mu-\epsilon}{kT}\right)}{1+\exp\left(\frac{\mu-\epsilon}{kT}\right)}\tag{6}\] である。
ではこの状態に入っている粒子の個数の期待値はといえば、 \[\langle N\rangle = 0\cdot P_0 + 1\cdot P_1\] だから、計算してやると、 \begin{align} \langle N\rangle &= \frac{\exp\left(\frac{\mu-\epsilon}{kT}\right)}{1+\exp\left(\frac{\mu-\epsilon}{kT}\right)}\\ &= \frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}\tag{7} \end{align} を得る。
(7)式がどういう意味だったのかもう一度書いておこう。(7)式は、温度\(T\)と化学ポテンシャル\(\mu\)を持っている熱浴と平衡状態にあるという状況のもとで、エネルギー\(\epsilon\)をもつ一つの状態に入っている粒子数の期待値のことである。
この期待値はフェルミ粒子がどのように分布しているかを示すから、これのことを
フェルミ・ディラック分布関数
という。このページでは\(f_{FD}(\epsilon)\)で表すことにした。 \[f_{FD}(\epsilon) = \frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}\tag{8}\] である。3.ボーズ粒子の分布関数
同じ状態に何個でも粒子が入れるボーズ粒子についても、同じように分布関数を求めることができる。つまり、一つの状態に着目して、別の状態は温度\(T\)、化学ポテンシャル\(\mu\)をもった熱浴であると考えるのだ。
ボーズ粒子の場合は、着目している状態に粒子が何個でも入ることができるから、分配関数は次のように計算する。粒子が一つその状態に入ったとき、エネルギーが\(\epsilon\)だから、\(N\)個入ったときには単純に\(N\epsilon\)になるだろう。だから、 \[Z=\sum_{N=0}^\infty\exp\left(\frac{N\mu-N\epsilon}{kT}\right)\tag{9}\] を計算すればいい。なんか難しそうだが、実は単なる等比級数である。わかりやすいように\(r=\exp\left(\frac{\mu-\epsilon}{kT}\right)\)とおくと、 \[Z=\sum_{N=0}^\infty r^N\tag{10}\] なので、|r|<1で収束すると仮定すれば、 \[Z=\frac{1}{1-r}=\frac{1}{1-\exp\left(\frac{\mu-\epsilon}{kT}\right)}\tag{11}\] を得る。
さて、次はこの状態に入っている粒子数の期待値を計算しよう。粒子数が\(n\)である確率は、 \[P_n=\frac{1}{Z}\exp\left(\frac{n\mu-n\epsilon}{kT}\right)\] だから、これを使って、期待値は次のように計算すればいい。 \begin{align} \langle N\rangle &= \sum_{n=0}^\infty nP_n\\ &=\frac{1}{Z}\sum_{n=0}^\infty n\exp\left(\frac{n\mu-n\epsilon}{kT}\right) \end{align} ちょっとめんどくさい計算が出てきてしまった。\(n\exp\left(\frac{n\mu-n\epsilon}{kT}\right)\)の和というのはどうやって計算すればいいだろうか。高校で受験数学をやった人なら、これの計算の仕方を覚えている人もいるのかもしれないが、今回は微分を使う方法でやってみよう。等比級数の和の公式 \[\sum_{n=0}^\infty r^n = \frac{1}{1-r}\] の両辺を\(r\)で微分すると、 \begin{align} \sum_{n=1}^\infty nr^{n-1} &= \frac{1}{(1-r)^2}\\ \sum_{n=0}^\infty nr^{n} &= \frac{r}{(1-r)^2}\\ \end{align} となることがわかる。これを使えば、粒子数の期待値の計算を続けることができる。 \begin{align} \langle N\rangle&=\frac{1}{Z}\sum_{n=0}^\infty n\exp\left(\frac{n\mu-n\epsilon}{kT}\right)\\ &=\frac{1}{Z}\frac{\exp\left(\frac{\mu-\epsilon}{kT}\right)}{\left(1-\exp\left(\frac{\mu-\epsilon}{kT}\right)\right)^2}\\ &=\frac{\exp\left(\frac{\mu-\epsilon}{kT}\right)}{1-\exp\left(\frac{\mu-\epsilon}{kT}\right)}\\ &=\frac{1}{\exp\left(\frac{\epsilon-\mu}{kT}\right)-1} \end{align} 結局こうなった。これは
ボーズ・アインシュタイン分布
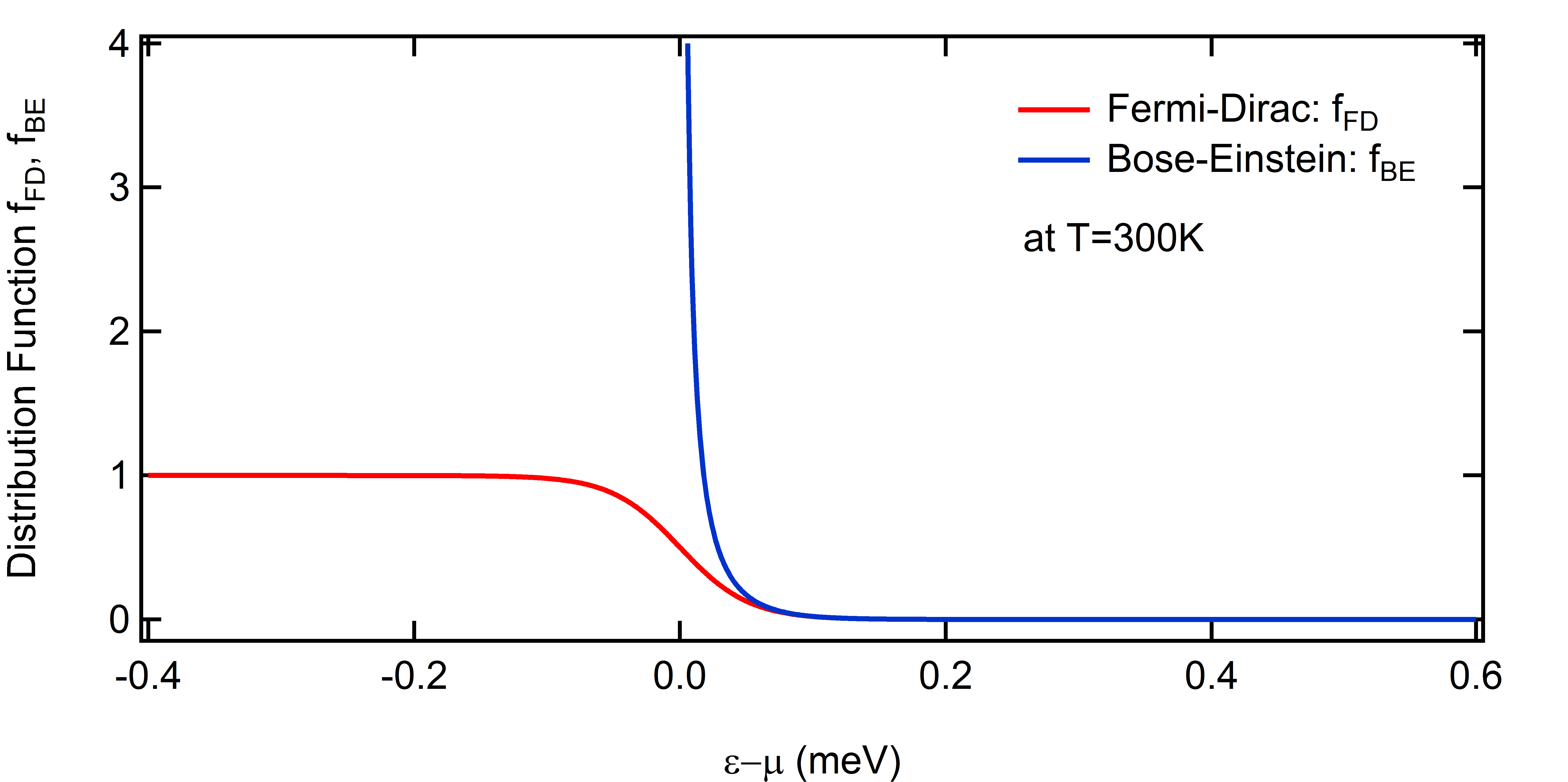
と呼ばれる。こちらは\(f_{BE}(\epsilon)\)と表すことにしよう。4.グラフ
最後にそれぞれのグラフを書いて終わりにする。