フェルミ準位とは何なのか
1.フェルミ準位とは
フェルミ準位を一文で言い表すなら、「電子が十分に入っている最高のエネルギーの値」とでもいえるだろう。具体的には、フェルミ-ディラック分布関数
\[f(\epsilon) = \frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}\tag{1}\] の中の\(\mu\)のことだ。この\(\mu\)は\(E_F\)と書かれることもあると思う。フェルミ分布は電子があるエネルギー\(\epsilon\)にいる確率を表していて、下のような形をしている。統計力学から導出できるので、その導出も別のページに書いておいた。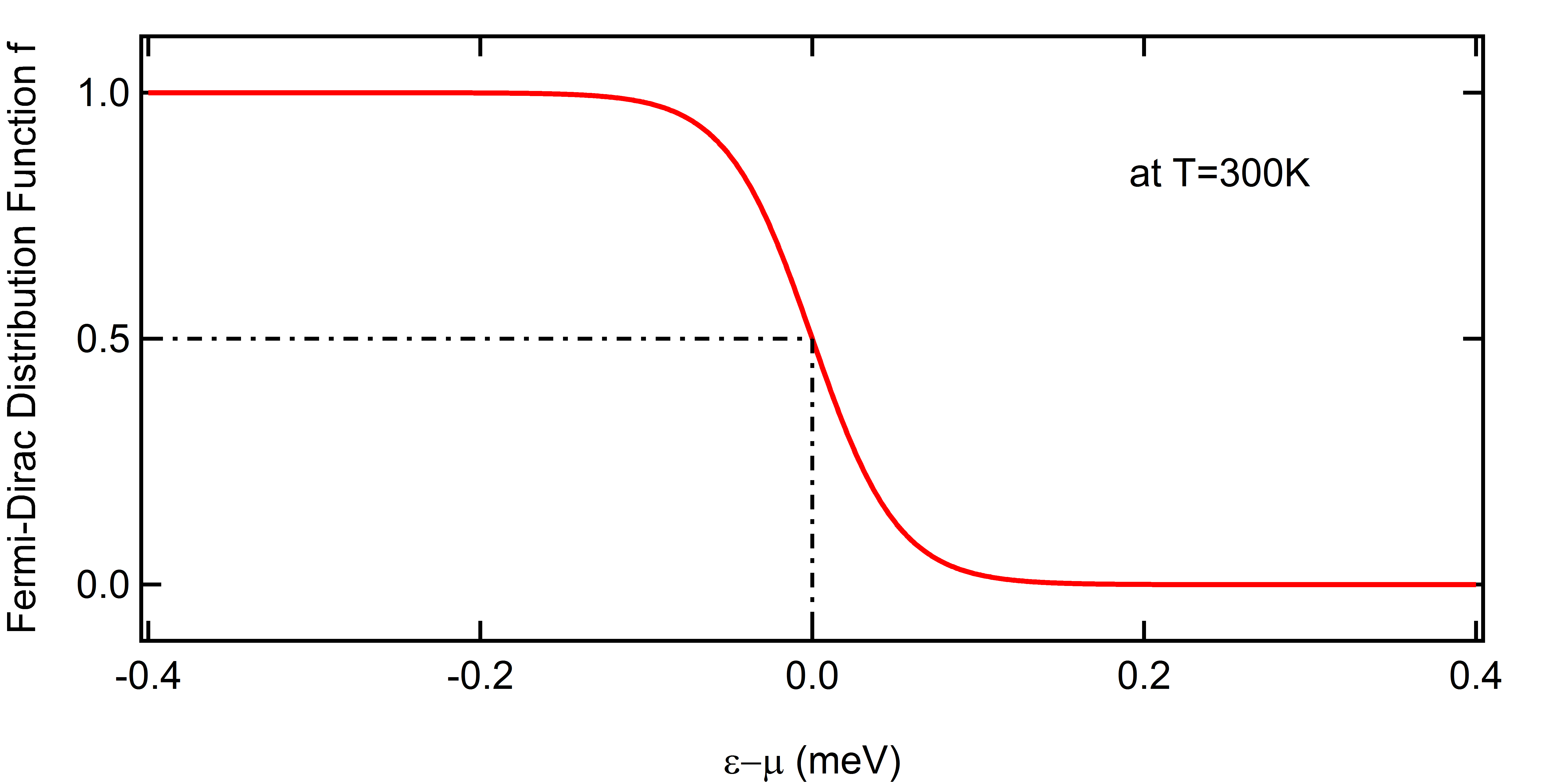
僕はこの分布関数を最初に知ったとき大きな誤解をしていたので、その間違えている考え方と正しい考え方をこのページにまとめておく。できる人はなんでこんなこと、と思うかも知れないけど、そういうときはこいつ頭悪いなと思いながらこのページを閉じてくれればいい。
2.積分しても1にならない!
僕は最初、フェルミディラック分布\(f(\epsilon)\)は「1つの電子があるエネルギーに存在する確率」を表している、と考えていた。 で、何の疑問も持たずに過ごしていたんだが、ある時ふと思いついた。「1つの電子があるエネルギーに存在する確率」を表すのだから、この\(f(\epsilon)\)を全エネルギーで積分したら1にならないとおかしいな、と思ったのだ。だって、一つの電子は必ずどこかのエネルギー準位に存在しているはずでしょ?と。
でも計算してみると、 \begin{align} \int_0^\infty f(\epsilon)d\epsilon &=\int_0^\infty \frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\ &= kT\int_{-\mu/kT}^\infty\frac{1}{1+e^x} dx ~~~~(\frac{\epsilon-\mu}{kT}=xとした)\\ &= kT\int_{-\mu/kT}^\infty\frac{e^{-x}}{1+e^{-x}} dx\\ &=kT\left[-\ln \left(1+e^{-x}\right)\right]_{-\mu/kT}^\infty\\ &=kT\ln \left(1+\exp\left(\frac{\mu}{kT}\right)\right)\tag{2} \end{align} となって、1とは程遠い結果がでてしまった。
これにはすごく困ってしまったのを覚えている。何回計算を見直してもあっていた。もしフェルミディラック分布が(1)のような形をとって、「1つの電子があるエネルギーに存在する確率」を表すとするならば、(2)で割らないと、物理的におかしなことになる。「1つの電子があるエネルギーに存在する確率」を表しているはずなのに、全てのエネルギーに存在する確率を足し合わせても1にならないのだから。
でも、そんなふうに(2)で割っているような文献は全然見当たらないし、悩みこんだ。
3.フェルミ-ディラック分布の意味
結局色々調べて、それまで知らなかった(避けていた)統計力学も勉強した結果、そもそもフェルミ-ディラック分布を「1つの電子があるエネルギーに存在する確率」と考えることが間違いだったことに気づけた。フェルミディラック分布とは、他の準位たちと熱平衡にある、ある一つの準位に着目したときに、そこに電子が入っている確率を表すのだ。つまり、他の準位からその準位に電子が出たり入ったりして、平均的に\(f(\epsilon)\)個の電子が存在しているという状況である。
だから、積分 \[\int f(\epsilon)d\epsilon\] というのは、「ある電子がどこかに存在している確率」というより、「それぞれの準位に電子が存在している平均的な個数の足し合わせ」といえる。個数を足したものなのだから、それは1になるわけがなくて、系に存在している電子の数になるべきだろう。
そして全電子数\(n\)は、考える系によって勝手に決まってくるものだ。固体中の電子の数は、それを作っている原子の種類によって決まるべきものなのだから。
ということで、 \[n=\int f(\epsilon)d\epsilon\] という式が成り立つはずだが、(2)から \[n=kT\ln \left(1+\exp\left(\frac{\mu}{kT}\right)\right)\tag{3}\] となる。この式はどういう意味だろうか。
実はこの(3)が、フェルミ準位\(\mu\)を決める式なのだ。(3)を\(\mu\)について解くことによって、フェルミ準位が計算される。つまり、フェルミ準位\(\mu\)というのは、電子数で決まる量である。
固体物理の教科書だと、この辺のことをあんまり教えてくれず、さらっと流されていることが多い気がする。僕が気づかなかっただけかも知れないけど。
4.状態密度も考慮に入れる
上の式、 \[n=\int f(\epsilon)d\epsilon\] は状態密度というのを考慮していない。\(\epsilon\to\epsilon+d\epsilon\)という幅に必ず1つの準位が存在しているとすればこのような式になるのだが、現実の世界はそんなに単純では無くて、エネルギーによってその準位の数が変化するのが普通である。そこで普通、\(\epsilon\to\epsilon+d\epsilon\)の間にある準位の数は、ある関数\(D(\epsilon)\)によって、\(D(\epsilon)d\epsilon\)と書かれる。だから、これは次のように書き直されるべきである。 \[n=\int f(\epsilon)D(\epsilon)d\epsilon\tag{4}\]
5.自由電子のフェルミエネルギー
自由電子の場合状態密度は \[D(\epsilon)=\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\sqrt{\epsilon}\tag{5}\] だった。(前回と前々回参照)そこで(4)式を計算してみると、 \begin{align} n&=\int f(\epsilon)D(\epsilon)d\epsilon\\ &=\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\int_0^\infty \frac{\sqrt{\epsilon}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon \end{align} となるが、こんな積分はできそうもない。そこで今回は簡単に絶対零度\(T\to 0\)の場合だけを考えよう。そうすると、フェルミ分布関数は階段関数になるから、 \begin{align} n&=\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\int_0^\mu\sqrt{\epsilon}d\epsilon\\ &=\frac{1}{3\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\mu^{3/2} \end{align} したがって、 \[\mu=\frac{2m}{\hbar^2}(3\pi^2 n)^{2/3}\tag{6}\] である。特に絶対零度でのフェルミ準位のことは