結晶における回折条件
1.波動の回折現象
波動性を持つものは何でも回折を起こす。それが電子であっても光であってもだ。量子力学から、全ての素粒子は粒子性と波動性を持っているから、これは全ての物質が何らかの形で回折現象を起こすといってもいいだろう。さて、下のような状況を考える。\(\b{k}\)という波数をもった光波が、その結晶中の粒子によって回折され、\(\b{k}'\)という波数となって出て行くようなものだ。
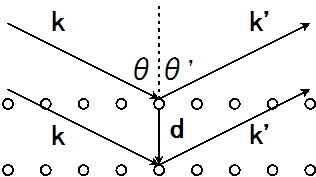
さて、今から知りたいのは、どの方向で波が強め合うかだ。一つの粒子から散乱される光は適当な方向へ飛んでいくが、出てきた波が\(\b{k}'\)の方向へ強くなる条件は、光路差による位相差を考えれば良くて、 \[d\cos\theta+d\cos\theta'= m\lambda\tag{1}\] を成り立たせれば良い。ただしmは整数である。図で\(\b{d}\)と\(\b{k}, \b{k}'\)の成す角はそれぞれ\(\theta, \pi-\theta'\)であるから、(1)は次のように書き直せる。 \[\b{d}\cdot(\b{k}-\b{k}')\frac{\lambda}{2\pi}=m\lambda\tag{2}\] ここで\(|\b{k}|=\frac{\lambda}{2\pi}\)であることを用いた。さらに簡単にすれば、 \[\b{d}\cdot(\b{k}-\b{k}')=2\pi m\tag{3}\] となる。かなり見やすくなってきたぞ。ここでちょっと一般化しよう。図の\(\b{d}\)だと隣同士の粒子との影響しか表せないが、実際にはもっと色々な粒子が回折を起こして、もっとたくさんの干渉を起こしているはずである。だからここで、\(\b{d}\)を並進ベクトル\(\b{T}\)に書き換える。 \[\b{T}\cdot(\b{k}-\b{k}')=2\pi m\tag{4}\] なんのことはない。ただ書き換えただけだ。当然この式も成り立っていないとだめだろう。
ところで、(4)式は「\((\b{k}-\b{k}')\)を並進ベクトルと内積を取ると、2πの整数倍となるときに回折が強まる」とみれるのではないか。そういえばそんなベクトルが前にあったな。逆格子ベクトル\(\b{G}\)である。 \[\exp(i\b{G}_i\cdot\b{T}) = \exp\left(i2\pi(u_1v_1+u_2v_2+u_3v_3)\right)=1 \] という性質をもつベクトルとして定義した(\(\b{G}\)というベクトルは、逆格子空間の格子点を示すベクトルで、いろんなベクトルがあり得る)。これを使えば、回折が強め合う条件は、 \[\b{k}-\b{k}'=\b{G} \tag{5}\] とかけるではないか!これは何を意味するかわかるだろうか?
実は、光の回折パターンを見れば、逆格子の形がわかる→結晶構造がわかるということを意味する。よくわからないきれいな結晶構造があったとして、そのある面にある方向\(\b{k}\)のX線を当てたとしよう。そのX線の回折が\(\b{k}'\)の方向で強くなっていたとすれば、一つの逆格子ベクトルが\(\b{k}-\b{k}'\)によって求まる。このようにして、逆格子ベクトルを見つけ出していけば、逆格子を構成することができるというわけ。逆格子の逆格子は元の結晶構造になるから、これで結晶構造が調べられる。
もちろん、現実には結晶の欠陥があったり、弾性衝突じゃなかったりして、そう簡単には行かないものの、概念的にはこういうことができるのだ。
2.ブリルアンゾーン
突然だが、(5)式を2乗しよう。 \[\begin{align} (\b{k}')^2&=(\b{k} - \b{G})^2 \\\\ k'^2&=k^2-2\b{k}\cdot\b{G} + G^2 \\\\ \b{k}\cdot\b{G} &= \frac{G^2}{2} \tag{6} \end{align}\] こうするとうまいこと\(\b{k}'\)が消えてくれる。(6)式も回折条件を表す式である。なぜこんなことをしたのかというと、
ブリルアンゾーン
(Brillouin Zone, BZ)を紹介したかったからだ。といっても、今紹介したからといって、特にまだ恩恵を感じることは無い気もする。しかし、回折条件を決める式(6)には何か物理的に重要な意味があるに違いない。
\(\b{k}\)を変数、\(\b{G}\)をある定ベクトルと見れば、(6)式は(\(\b{G}\)に対応する色々な)平面を表すことがわかる。これを境界として逆格子空間を分割したもの一つ一つが、ブリルアンゾーンである。つまり、ブリルアンゾーンの境界で、回折が強く起こるわけだ。このブリルアンゾーンは実はブロッホの定理と密接に関係していて、逆格子空間の原点まわりのブリルアンゾーンの中に、固体電子の全ての波動関数が存在する。これがブリルアンゾーンが非常に重要な理由である。(ブロッホの定理から説明したページ)
まだ意味はわからなくても大丈夫だと思う。図はそのうち追加する。