逆格子・逆格子ベクトルの例
0.逆格子ベクトル
ある基本並進ベクトルの組\(\b{a}_1,\b{a}_2,\b{a}_3\)から、逆格子ベクトルの組が下のように計算できるのだった。 \[ \b{b}_1 = 2\pi \frac{\b{a}_2 \times \b{a}_3}{\b{a}_1\cdot(\b{a}_2\times\b{a}_3)},~~\b{b}_2 = 2\pi \frac{\b{a}_3 \times \b{a}_3}{\b{a}_1\cdot(\b{a}_2\times\b{a}_3)}, ~~\b{b}_1 = 2\pi \frac{\b{a}_1 \times \b{a}_2}{\b{a}_1\cdot(\b{a}_2\times\b{a}_3)}\tag{1}\] 今回は、この逆格子ベクトルに関して、具体的な例を見ていくことにする。1.単純立方格子
最初は簡単な例を考えてみる。例えば単純立方格子なんかどうだろうか。つまり、\(\b{a}_1,\b{a}_2,\b{a}_3\)がどれも直交していて、大きさも等しいようなものである。簡単のため、xyz方向の単位ベクトル\(\hat{\b{x}},\hat{\b{y}},\hat{\b{z}}\)を用いて、 \[\b{a}_1=a\hat{\b{x}},~~\b{a}_2=a\hat{\b{y}},~~\b{a}_3=a\hat{\b{z}}\] としよう。これを(1)式に入れて、x,y,zが右手系だとすれば、\(\hat{\b{x}}\times\hat{\b{y}}=\hat{\b{z}}\)などが成り立つので、 \[\b{b}_1=\frac{2\pi}{a} \hat{\b{x}}, ~~\b{b}_2=\frac{2\pi}{a} \hat{\b{y}}, ~~\b{b}_3=\frac{2\pi}{a} \hat{\b{z}}\] となる。立方格子の逆格子は立方格子ということだ。ちょうど1の逆数が1であるようなことだろう。
計算すればわかるが、基本並進ベクトルが直行するような格子の逆格子の基本ベクトルは、やはりそれぞれ直交する。
2.体心立方格子
次は体心立方格子を考えてみよう。これは図が必要だな。Body Centered Cubicの略でbccと呼ばれたりする。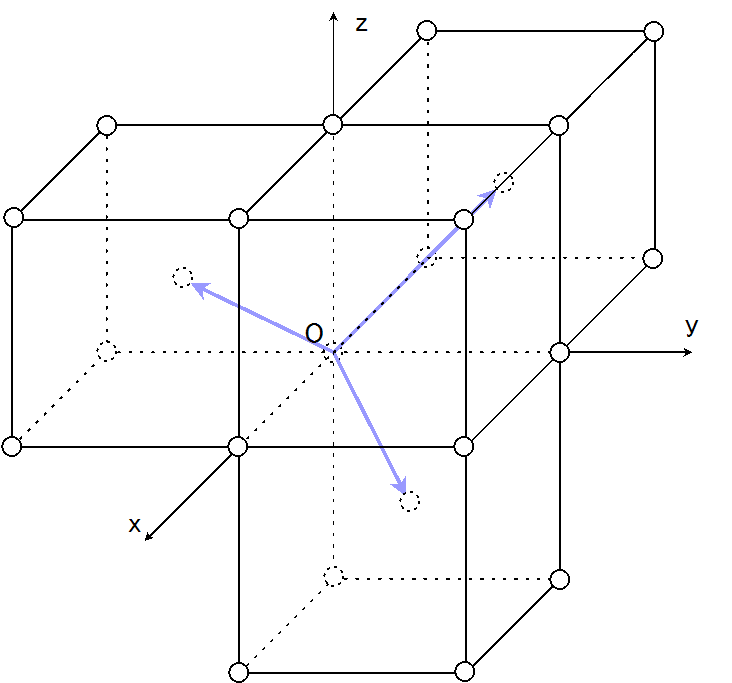
図で示した水色の矢印がbccの基本並進ベクトルである。ちょっと考えれば、このベクトルの整数倍で、全ての格子点を表せることがわかるはずだ。もちろん取り方はこれだけでは無いが、とりあえずこれで行こう。
立方体の一辺を\(a\)とすれば、水色のベクトルは、 \[ \left\{\begin{align} \b{a}_1&=\frac{a}{2} (\hat{\b{x}}+\hat{\b{y}}-\hat{\b{z}}) \\\\ \b{a}_2&=\frac{a}{2} (-\hat{\b{x}}+\hat{\b{y}}+\hat{\b{z}}) \\\\ \b{a}_3&=\frac{a}{2} (\hat{\b{x}}-\hat{\b{y}}+\hat{\b{z}}) \end{align}\right. \] とかける。これを(1)式に入れて計算していこう。 \[ \begin{align} \b{a}_2 \times \b{a}_3 &= \left(\frac{a}{2}\right)^2 (-\hat{\b{x}}+\hat{\b{y}}+\hat{\b{z}})\times(\hat{\b{x}}-\hat{\b{y}}+\hat{\b{z}}) \\\\ &= \left(\frac{a}{2}\right)^2 (\hat{\b{x}}+\hat{\b{y}}) \\\\ \b{a}_1 \cdot (\b{a}_2\times\b{a}_3) &= \left(\frac{a}{2}\right)^3 (1+1) \\\\ &= \frac{a^3}{4} \end{align}\] だから、 \[\begin{align} \b{b}_1&=2\pi \frac{\b{a}_2 \times \b{a}_3}{\b{a}_1\cdot(\b{a}_2\times\b{a}_3)} \\\\ &=2\pi \frac{\left(\frac{a}{2}\right)^2 (\hat{\b{x}}+\hat{\b{y}})}{\frac{a^3}{4}} \\\\ &=\frac{2\pi}{a}(\hat{\b{x}}+\hat{\b{y}}) \end{align}\] のように計算できる。他の2つも同様にやると、 \[ \left\{\begin{align} \b{b}_1&=\frac{2\pi}{a} (\hat{\b{x}}+\hat{\b{y}}) \\\\ \b{b}_2&=\frac{2\pi}{a} (\hat{\b{y}}+\hat{\b{z}}) \\\\ \b{b}_3&=\frac{2\pi}{a} (\hat{\b{z}}+\hat{\b{x}}) \end{align}\right.\tag{2} \] とまあかなりきれいな形になる。これは実はすごく面白い結果だ。
3.面心立方格子
まずは面心立方格子の図を書いておく。面心立方格子は、立方体の頂点と各面の中心を格子点とする格子である。Face Centered Cubicからfccとも言われる。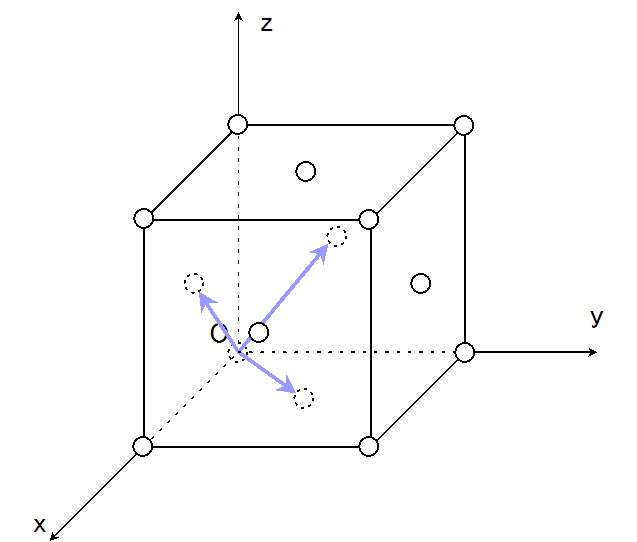
と、いうことはfccの逆格子はbccに違いない。実際に計算すれば、、 \[ \left\{\begin{align} \b{b}_1&=\frac{2\pi}{a} (\hat{\b{x}}+\hat{\b{y}}-\hat{\b{z}}) \\\\ \b{b}_2&=\frac{2\pi}{a} (-\hat{\b{x}}+\hat{\b{y}}+\hat{\b{z}}) \\\\ \b{b}_3&=\frac{2\pi}{a} (\hat{\b{x}}-\hat{\b{y}}+\hat{\b{z}}) \end{align}\right. \] となっていることが確認できる。