Blochの定理に関する補足とブリルアンゾーンの意味
1.Blochの定理についておさらい
Blochの定理とは、一つの電子が周期的なポテンシャルを受ける場合に、その波動関数が、 \[\psi_\b{k}(\b{r}+\b{R})=e^{i\b{k}\cdot\b{R}}\psi_\b{k}(\b{r})\tag{1}\] を満たすという定理だった。\(\b{R}\)は結晶の並進ベクトル。(1)式から、周期ポテンシャル中の波動関数は、並進演算子\(\hat{T}_\b{R}\)の固有関数になっていて、その固有値が\(e^{i\b{k}\cdot\b{R}}\)であることがわかる。なぜなら、(1)は \[\hat{T}_\b{R}\psi_\b{k}(\b{r})=e^{i\b{k}\cdot\b{R}}\psi_\b{k}(\b{r})\tag{1'}\] ということを示しているのにほかならないからだ。(だからといって別にこれ以上意味があるわけでも無いのだが。)Blochの定理はまた、\(\b{R}\)について周期的な関数\(u_\b{k}(\b{r})=u_\b{k}(\b{r}+\b{R})\)を使って、 \[\psi_\b{k}(\b{r})=e^{i\b{k}\cdot\b{r}}u_\b{k}(\b{r})\tag{2}\] とも書ける。こちらのほうが使われることが多いかもしれない。
※ブリルアンゾーンの説明を見に来た人は、2は飛ばしてくれて構わない。
2.Blochの定理の\(\b{k}\)の決まり方
Blochの定理における、並進演算子の固有値に相当する\(\b{k}\)という量は何によって決定されるかわかるだろうか?定理だけを知っていても、\(\b{k}\)が何者なのか知っておかなければ意味がない。\(\b{k}\)というのは、シュレディンガー方程式によって決まる量だ。
具体的には、(2)をシュレディンガー方程式に代入して、 \begin{align} \left(-\frac{\hbar^2}{2m}\nabla^2 + V(\b{r})\right)\left(e^{i\b{k}\cdot\b{r}}u_\b{k}(\b{r})\right) &= Ee^{i\b{k}\cdot\b{r}}u_\b{k}(\b{r})\\ -\frac{\hbar^2k^2}{2m}u_\b{k}(\b{r})-i\frac{\hbar^2\b{k}}{2m}\cdot\nabla u_\b{k}(\b{r}) -\frac{\hbar^2}{2m}\nabla^2u_\b{k}(\b{r})+V(\b{r})u_\b{k}(\b{r})&= Eu_\b{k}(\b{r})\\ \left(-\frac{\hbar^2}{2m}(\nabla+i\b{k})^2+V(\b{r})\right)u_\b{k}(\b{r})&= Eu_\b{k}(\b{r})\tag{3} \end{align} という複雑な式を解いたときに、解が存在する条件として決定されるのが、\(\b{k}\)である。
式の形だけを見ると、最初のシュレディンガー方程式よりも難しくなったような気がしてしまうが、\(u(\b{r})\)というのは\(\b{R}\)に対して周期的なので、(3)を解くのは一周期分(基本単位胞分)だけで良くなっているのだ。少し話は飛んだが、もとのシュレディンガー方程式が無限遠まで解かなければいけなかったことに比べれば、とても簡単になっていてBlochの定理の有効性がよく分かる。
3.ブリルアンゾーン
もう一度最初のBlochの定理 \[\psi_\b{k}(\b{r}+\b{R})=e^{i\b{k}\cdot\b{R}}\psi_\b{k}(\b{r})\tag{1}\] を見直そう。天下り的ではあるが、\(\b{k}\)に対して、適当な逆格子ベクトル\(\b{G}\)を足すと、 \[\psi_{\b{k}+\b{G}}(\b{r}+\b{R})=e^{i(\b{k}+\b{G})\cdot\b{R}}\psi_\b{\b{k}+\b{G}}(\b{r})\] さらに逆格子ベクトルの\(\b{G}\cdot\b{R}=2\pi n\)という性質 (これが成り立つことが逆格子ベクトルの定義みたいなものだった) から、 \[\psi_{\b{k}+\b{G}}(\b{r}+\b{R})=e^{i\b{k}\cdot\b{R}}\psi_\b{\b{k}+\b{G}}(\b{r})\tag{4}\] となる。
(4)はとても大事な結果である。これは\(\psi_\b{k}\)と\(\psi_{\b{k}+\b{G}}\)という状態が、並進演算子\(\hat{T}_\b{R}\)に対して同じ固有値を持っていることを表しているのだ。つまり、位相の違いはあるかも知れないから近似イコールで表すが、 \[\psi_{\b{k}+\b{G}}\fallingdotseq \psi_\b{k}\] みたいなことを意味している。
ところで、さっき書いたように、\(\b{k}\)はシュレディンガー方程式の解が存在するように決まるもので、ハミルトニアンのエネルギー固有値\(E\)と\(E=E(\b{k})\)のように結びついた形となる。ということは、\(\psi_\b{k}\)と\(\psi_{\b{k}+\b{G}}\)が同じ固有値\(\b{k}\)を共有しているのであれば、この2つの状態は同じエネルギー状態にある。
だから、周期ポテンシャル中の一つの電子について一見違うように見える波動関数、\(\psi_\b{k}\)と\(\psi_{\b{k}+\b{G}}\)は、(位相の違いを無視すると) 全く同じ状態を表すと言ってもいいだろう。
ということは、周期ポテンシャル中の一つの電子については、\(\b{k}\)空間の全領域を考える必要は全く無いということになる。だって、ある\(\b{k}_0\)という固有値を持つ状態がどんな状態なのかわかれば、任意の逆格子ベクトル\(\b{G}\)を\(\b{k}_0\)に足した\(\b{k}_1=\b{k}_0+\b{G}\)という固有値に対応する状態がどんな状態なのかも、自動的に分かってしまうのだから。
うまいこと\(\b{k}\)空間の一部を考えるためには、どのようにするのが便利だろうか?というときに現れるのが
ブリルアンゾーン
である。説明するために、まずは簡単に、下の図のような二次元の正方格子を考えよう。\(\b{b}_1,\b{b}_2\)は逆格子ベクトルの基底 (逆格子空間の基本並進ベクトル) である。任意の逆格子ベクトルは\(\b{G}=n_1\b{b}_1+n_2\b{b}_2\)と書けるのだ。
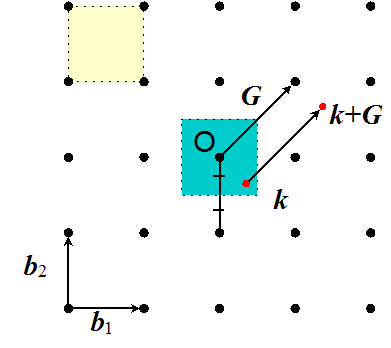
しかし、原点を真ん中にとった青い領域を使うと便利なことが多い。そこで、この青い領域は (第一)
ブリルアンゾーン
と特別な名前がついている。4.ブリルアンゾーンについてのまとめ
とにかく大事なことは、青い領域で示したブリルアンゾーン中の波数だけを考えれば、周期ポテンシャル中の電子の波動関数は全て記述できるということだ。そしてそのことは、ブロッホの定理によって保証される。さて、具体的にブリルアンゾーンをどうやって作るかというのを最後に書いて終わりにしよう。正方格子ならまだ思いつきで書けるかもしれないが、例えば面心立方格子とかでそれをやろうというのは、少なくとも僕には難しい。
一般的にブリルアンゾーンを作るには、逆格子空間で原点から最近接の格子点へ線を引き、その線の垂直二等分面をとる。その垂直二等分面で囲まれた領域がブリルアンゾーンである。上で示した図も、その方法で作られていることがわかるだろう。
ちなみに、この方法で作ったcellのことは、Wigner-Seitz Cellと呼ばれる。説明がわかりにくかったら、Wigner-Seitz Cellで検索すればわかりやすい図があるはずだ。