測地的曲率と測地線
1.測地的曲率
今回は測地的曲率
の性質や、測地線
について書こうと思う。曲面上曲線の曲率のページでも紹介したが、まずは曲面に拘束された曲線の測地的曲率\(\kappa_g\)が、どのように定義される量だったか確認しよう。曲面\(\b{p}(u^1,u^2)\)上に定義された曲線\(\b{x}(s)=\b{p}(u^1(s),u^2(s))\)の測地的曲率とは、曲線の曲率ベクトル\(\b{x}''(s)\)の接平面成分であり、その点での単位法線ベクトル\(\b{N}\)を使って、 \[\kappa_g = |\b{x}''-(\b{x}''\cdot\b{N})\b{N}|\tag{1}\] とかける。下の図のように曲率を分解するわけである。ちなみに、\(\b{x}''\cdot\b{N}=\kappa_n\)は法曲率と呼ばれる。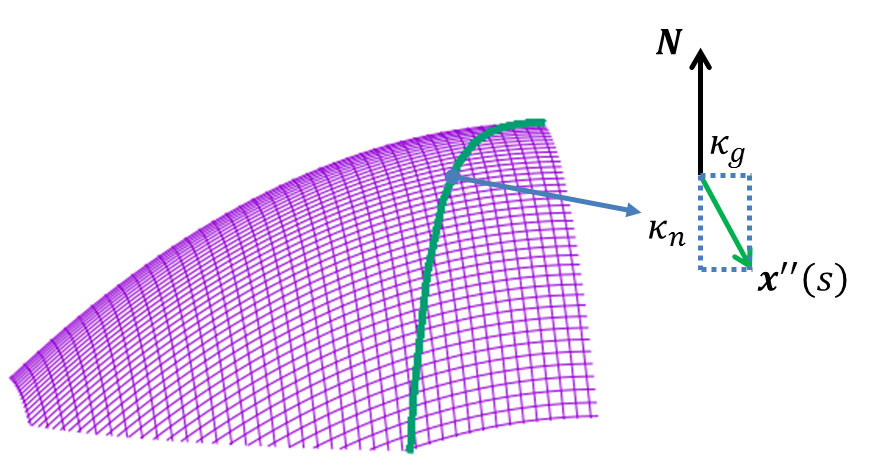
それと、今回からはシグマ記号が増えすぎて大変なことになるので、Einsteinの規約を使う。Einsteinの規約とは、同じ添字が上下に出てきたときは、自動的に和をとるというルールだ。例えば今回考えるような曲線の接ベクトルは、合成関数の微分を使って、 \[\frac{d\b{x}}{ds} = \sum_i\frac{\partial\b{p}}{\partial u^i}\frac{du^i}{ds}\tag{2}\] のように計算できるが、これを \[\frac{d\b{x}}{ds} = \frac{\partial\b{p}}{\partial u^i}\frac{du^i}{ds}\tag{3}\] と書くのがEinsteinの規約である。
結果は、測地的曲率が \[ \kappa_g=\left|\begin{array}{cc} \frac{du^1}{ds} & \Gamma^1_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^1}{ds^2} \\\\ \frac{du^2}{ds} & \Gamma^2_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^2}{ds^2} \end{array}\right|\sqrt{g} \] となり、測地線を求めるための微分方程式は \[\Gamma^k_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^k}{ds^2} = 0\] である。
2.測地的曲率を求める
測地的曲率を具体的に求めてみよう。測地的曲率を、曲面の第一基本量\(g_{ij}\)・第二基本量\(h_{ij}\)・パラメータ\(u^i\)の微分\(\frac{du^i}{ds}\)で表すことが目標だ。(1)式から、測地的曲率を求めるには、 \[\b{k}_g = \b{x}''-\kappa_n\b{N} = \b{x}''-(\b{x}''(s)\cdot\b{N})\b{N}\tag{4}\] というベクトルの大きさを求められれば良い。そこで注目するのは、このベクトル\(\b{k}_g\)が\(\b{N}\)や\(\b{x}'\)に対して垂直である、ということだ。\(\b{N}\)に垂直なのは定義からあたりまえだが、\(\b{x}'\)というベクトルにも垂直なのは意外かもしれない。しかし、\(\b{x}'\)というのは要するに曲線の接ベクトルのことなので、曲線の主法線ベクトル\(\b{x}''\)や、曲面の法線ベクトル\(\b{N}\)に垂直なのだ。 だからその大きさは、\(\b{N},\b{x}'\) (2つとも単位ベクトルだったことに注意しておこう。) に垂直な単位ベクトル\(\b{a}=\b{N}\times\b{x}'\)を使えば、符号をとりあえず無視して\(\kappa_g = \b{k}_g \cdot\b{a}\)によって求められる。よって \begin{align} \kappa_g &= (\b{x}''-(\b{x}''(s)\cdot\b{N})\b{N})\cdot(\b{N}\times\b{x}') \\ &= \b{x}''\cdot(\b{N}\times\b{x}')&(\because \b{N}\cdot(\b{N}\times\b{x}')=0)\\ &= \b{x}''\cdot(\b{N}\times\b{x}')\tag{4} \end{align} となる。
次に\(\b{x}',\b{x}''\)を曲面における自然な基底の組\(\left\{\b{p}_1,\b{p}_2,\b{N}\right\}\)ただし \(\b{p}_i = \frac{\partial \b{p}}{\partial u^i}\) によって表していこう。
\(\b{x}'\)の方は(3)式でもうできていて、 \[\b{x}'=\frac{du^i}{ds}\b{p}_i\tag{5}\] となっている。
\(\b{x}''\)のほうは(5)式をもう一度微分しなくてはいけなくて少し面倒だが、次のように計算できる。前回のGauss-Codazzi方程式、 \[ \frac{\partial \b{p}_i}{\partial u^j} = \sum_k \Gamma^k_{~ij}\b{p}_k + h_{ij}\b{N}\tag{6} \] を用いると、(\(\Gamma^k_{~ij}\)は第一基本量から決まる関数である) \begin{align} \b{x}''&= \frac{d}{ds}\left(\frac{d\b{x}}{ds}\right) \\ &= \frac{d}{ds}\left(\b{p}_i\frac{du^i}{ds}\right) \\ &= \frac{d\b{p}_i}{ds}\frac{du^i}{ds} + \b{p}_i\frac{d^2u^i}{ds^2} \\ &= \frac{\partial\b{p}_i}{\partial u^j}\frac{du^j}{ds}\frac{du^i}{ds} + \b{p}_i\frac{d^2u^i}{ds^2} \\ &= \left(\Gamma^k_{~ij}\b{p}_k + h_{ij}\b{N}\right)\frac{du^j}{ds}\frac{du^i}{ds} + \b{p}_i\frac{d^2u^i}{ds^2}\tag{7} \end{align} のように書ける。(5)と(7)を\(\kappa_g\)を求める式(4)に代入して計算していくと、 \begin{align} \kappa_g &= (\b{N}\times\b{x}')\cdot\b{x}'' \\ &= \left(\b{N}\times\b{p}_l\frac{du^l}{ds}\right)\cdot\left\{\left(\Gamma^k_{~ij}\b{p}_k + h_{ij}\b{N}\right)\frac{du^j}{ds}\frac{du^i}{ds} + \b{p}_i\frac{d^2u^i}{ds^2}\right\} \\ &=\left(\b{N}\times\b{p}_l\frac{du^l}{ds}\right)\cdot\left\{\Gamma^k_{~ij}\b{p}_k\frac{du^j}{ds}\frac{du^i}{ds} + \b{p}_k\frac{d^2u^k}{ds^2}\right\} &(\because \b{N}\cdot(\b{N}\times\b{x}')=0)\\ &= \left(\b{N}\times\b{p}_l\frac{du^l}{ds}\right)\cdot\left(\Gamma^k_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^k}{ds^2}\right)\b{p}_k \\ &=\left\{\left(\b{N}\times\b{p}_l\frac{du^l}{ds}\right)\cdot\b{p}_k\right\}\left(\Gamma^k_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^k}{ds^2}\right)\\ &=\left\{\left(\b{N}\times\b{p}_l\right)\cdot\b{p}_k\right\}\left(\Gamma^k_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^k}{ds^2}\right)\frac{du^l}{ds}\tag{8}\\ \end{align} とまあこんな感じになる。さらにベクトルの内積の部分について考えると、ベクトル三重積の性質から、 \[\left(\b{N}\times\b{p}_l\right)\cdot\b{p}_k = \b{N}\cdot(\b{p}_l\times\b{p}_k)\tag{9}\] と書き直せる。(9)の外積は\(l,k\)が異なるときにのみ0でなくなることに注意しておこう。ここで \[|\b{p}_1\times\b{p}_2|^2 = \det\left(\begin{array}{cc} g_{11} & g_{12} \\ g_{21} & g_{22} \end{array}\right) = g,\] \[\b{N} = \frac{\b{p}_1\times\b{p}_2}{\sqrt{g}}\] であったことを思い出す (接平面の記事参照) と、\(l=1,k=2\)のとき(9)は、 \[\b{N}\cdot(\b{p}_1\times\b{p}_2) = \sqrt{g}\] となるし、逆の時には、 \[\b{N}\cdot(\b{p}_2\times\b{p}_1) = -\sqrt{g}\] である。これを(8)に代入して整理すると、測地的曲率は \[ \kappa_g=\left|\begin{array}{cc} \frac{du^1}{ds} & \Gamma^1_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^1}{ds^2} \\\\ \frac{du^2}{ds} & \Gamma^2_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^2}{ds^2} \end{array}\right|\sqrt{g}\tag{9} \] のように行列式を使って表せることがわかる。
(9)のように行列式で表したからと言って、具体的な曲面上の曲線に対して(9)で測地的曲率を計算するのは手間がかかりすぎる。具体的な問題を解かないといけないときには、測地的曲率の定義式(4)から計算するほうが遥かに簡単だろう。
3.測地線
測地線とは、測地的曲率が0であるような曲線のことだ。曲面上における「直線」と言ってもいいだろう。測地的曲率が0である、という条件は、(8)式から、 \[\Gamma^k_{~ij}\frac{du^j}{ds}\frac{du^i}{ds} + \frac{d^2u^k}{ds^2} = 0 \tag{10}\] とかける。(もちろん\(\frac{du^l}{ds}=0\)でもいいのだが、これではsに対して\(u^l\)が定数になってしまって曲線にならない。)
この(10)式は