曲面の第二基本形式と曲率
1.曲面の曲がり具合
今回は曲面の曲がり具合、つまり曲率について説明する。ある一つの点での曲面の曲がり具合と言うのは、どのように表現するのが適当だろう?考えられるひとつの方法は、調べたい点Aでの接平面を考えて、その点から微小距離だけ離れた点A'からその接平面までの距離dを調べる、というものである。これによって、その点での曲面がどれだけ平面的でないか、つまり「曲がっている」かを調べることができる。
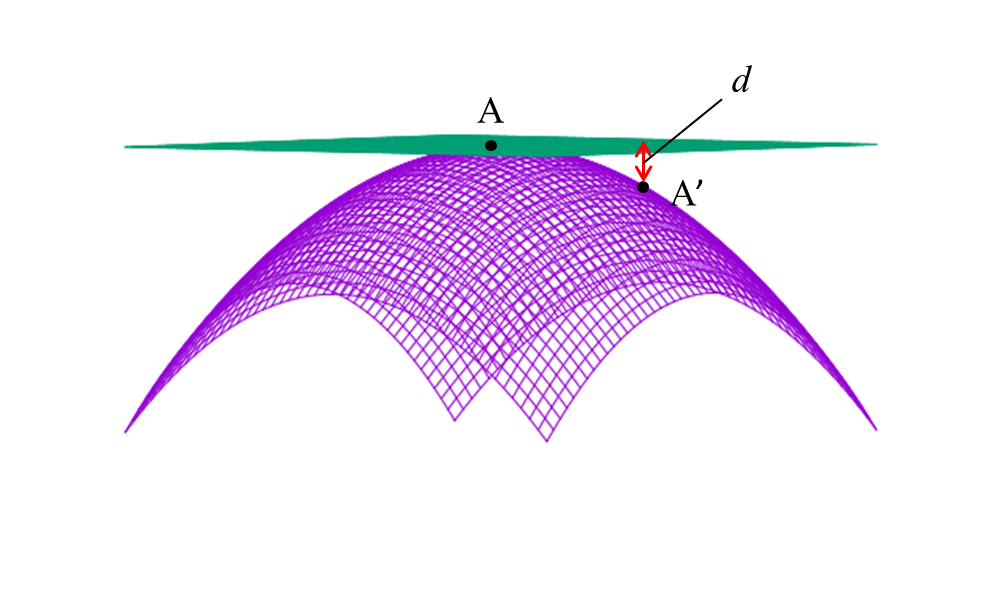
考える2つの点は、\(A:\b{p}(u^1,u^2)\), \(A':\b{p}(u^1+du^1,u^2+du^2)\)とする。接平面とA'の間の距離dは、Aにおける接平面の単位法線ベクトルを\(\b{N}\)とすれば、 \[d=\left\{~\b{p}(u^1+du^1,u^2+du^2) - \b{p}(u^1,u^2)~\right\}\cdot\b{N}\tag{1}\] とかける。\(du^1,du^2\)が小さいことを踏まえて、テイラー展開してみよう。すると、 \[d\cong\left\{\frac{\partial\b{p}}{\partial u^1}du^1 + \frac{\partial\b{p}}{\partial u^2}du^2+\frac{\partial^2\b{p}}{\partial {u^1}^2}\frac{(du^1)^2}{2}+\frac{\partial^2\b{p}}{\partial u^1\partial u^2}du^1du^2+\frac{\partial^2\b{p}}{\partial {u^2}^2}\frac{(du^2)^2}{2} \right\}\cdot\b{N}\tag{2}\] となる。\(\frac{\partial\b{p}}{\partial u^i}\)というベクトルは、前回紹介した接ベクトルそのものなので、これは\(\b{N}\)していなくてはいけない。よって、 \[d\cong\frac{1}{2}\left(\frac{\partial^2\b{p}}{\partial {u^1}^2}(du^1)^2+2\frac{\partial^2\b{p}}{\partial u^1\partial u^2}du^1du^2+\frac{\partial^2\b{p}}{\partial {u^2}^2}(du^2)^2\right)\cdot\b{N}\tag{3}\] となり、実際のところ、この\(d\)はh,du^2の二次の項を中心として決定されることがわかる。
2.第二基本形式
新しく \[h_{ij} = \frac{\partial^2\b{p}}{\partial u^i\partial u^j}\cdot\b{N}\tag{4}\] とと記号を定義すると、 \[2d\approx\sum_i\sum_jh_{ij}du^idu^j\tag{5}\] のように書ける。この式は曲面の曲がり具合を端的に表す式なので、特別に名前がついていて、 \[H=\sum_i\sum_jh_{ij}du^idu^j\tag{6}\] は曲面の第二基本形式
と呼ばれる。また、この\(H=0\)となるような方向(\(du^1,du^2\)の組み合わせ)のことを、主接線方向
という。H=0となるのは、一番接平面と曲面が一致している時なのだから、このような名前が付いているのも納得がいく。3.曲面の曲率について少し考えてみる
そろそろ曲面の曲率
という量も定義してみたいだが、どういうふうに定義したらいいのかも検討もつかない。曲線の時には円による近似によって定義し求めたが、曲面となると球面によって近似すれば良いのだろうか?でも近似球面を見つけるのは結構大変そうだ。曲線を円によって近似した時には、接触平面上に円があることが予想できたから、その中心にある程度あたりをつけて求めていくことができたが、今回は球面なのでそんなことはできない。つまり、球面の中心にあたりをつけることはかなり難しそうなのだ。もしやるとすれば、4次元空間に3次元のなにか接触平面のようなものを考えてやるしかないように思える。しかしそんなものを直感的にイメージすることができないから困ってしまう。
そこで、少し方針を変えて、曲面上の曲線の曲率を考えて、それから曲面の曲率を定義してみよう。
4.曲面上曲線の曲率 - 法曲率と測地的曲率
曲面\(\b{p}=\b{p}(u^1,u^2)\)の上に存在して、弧長パラメータsによって表された曲線 \[\b{x}(s)=\b{p}(u^1(s),u^2(s))\] を考えよう。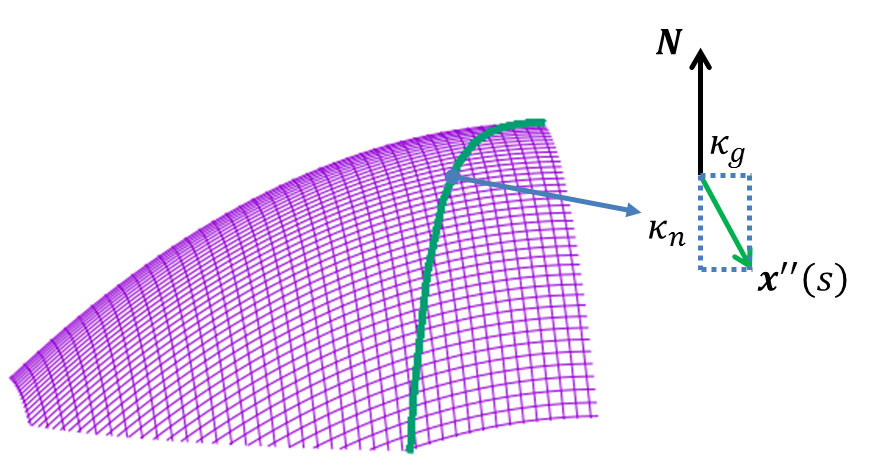
曲率ベクトル
と呼ぶことにしよう。曲率ベクトル\(\b{x}''\)は、曲線の主法線ベクトル\(\b{n}\)の方向を向いていて、 \[\b{x}''=\kappa\b{n}\tag{7}\] である。ところで、図のように曲面の単位法線ベクトル\(\b{N}\)とこの曲線の主法線ベクトル\(\b{n}\)は、当たり前だが一般に一致しない。そこで、次のように、曲率ベクトル\(\b{x}''\)を曲面に垂直な方向と平行な方向に分解してみよう。 \begin{align} \kappa_n &= \b{x}''\cdot\b{N} \\ \kappa_g &= |\b{x}''-\kappa_n\b{N}| \end{align} このように計算される\(\kappa_n\)は
法曲率
、\(\kappa_g\)は測地的曲率
と呼ばれる。 もともと曲面が曲がっていないとき、つまり平面のときには、法曲率の方は必ず0になることはすぐに分かるだろう。これを踏まえると、法曲率は曲線がそもそも持っている曲がり具合というよりも、曲面に拘束されているために現れてしまうものだと考える事ができ、よってこれは曲面自体の曲がり具合を表していると解釈できる。一方で、測地的曲率は曲面上に生活している人から見た時の、曲線の曲率のようなものである。今回はこの辺にしておいて、次回から具体的に法曲率を計算したり、性質を調べたりしていこう。
おまけ
第二基本形式には、別の表現方法もある。次回使うことになるので、ついでだし紹介しよう。係数 \[h_{ij} = \frac{\partial^2\b{p}}{\partial u^i\partial u^j}\cdot\b{N}\tag{4}\] を書き換えるために、接ベクトルと法線ベクトルが直交することを使う。 \[\frac{\partial\b{p}}{\partial u^i}\cdot\b{N} = 0\] この両辺をもう一度微分して、 \[h_{ij}=\frac{\partial^2\b{p}}{\partial u^i\partial u^j}\cdot\b{N}=-\frac{\partial\b{p}}{\partial u^j}\cdot\frac{\partial\b{N}}{\partial u^i}\] を得る。つまり、 \[\sum_i\sum_jh_{ij}du^idu^j = -\sum_i\sum_j\frac{\partial\b{p}}{\partial u^j}\cdot\frac{\partial\b{N}}{\partial u^i}du^idu^j\] である。ここで\(\b{p},\b{N}\)の全微分を考えると、 \[d\b{p} = \frac{\partial\b{p}}{\partial u^1}du^1 + \frac{\partial\b{p}}{\partial u^2}du^2\] \[d\b{N} = \frac{\partial\b{N}}{\partial u^1}du^1 + \frac{\partial\b{N}}{\partial u^2}du^2\] だから、 \[\sum_i\sum_jh_{ij}du^idu^j=-d\b{p}\cdot d\b{N}\] とも書けることがわかる。