曲率・曲率半径と接触平面
0.曲率とは
曲率とは、曲線がある一点でどれだけ「曲がっている」かを定量的に表す量である。曲がり加減を表すためには色々方法が考えられるだろうが、曲線の曲率といったときには、曲線のある点周辺を近似する円の半径の逆数のことを指す。逆に、この円の半径は曲率半径\(\rho\)と呼ばれる。今回は、この曲率や曲率半径がどうやって表されるか考えよう。結論だけ先に書くと、弧長\(s\)をパラメータとして表された曲線\(\b{x}(s)\)の曲率半径は \[\frac{1}{\rho} = \left|\frac{d^2\b{x}}{ds^2}\right|\] となる。弧長sではなくて、一般的なパラメータで表した曲線\(\b{x}(t)\)の場合は、 \[\frac{1}{\rho} = \left|\frac{d\b{x}}{dt}\times\frac{d^2\b{x}}{dt^2}\right|/\left|\frac{d\b{x}}{dt}\right|^3\] である。1.接触平面
本当はすぐにでも曲率の話をしたいところだが、前準備として、接触平面
という概念について説明しておこう。接触平面とは、ある一点\(s_0\)でその曲線が乗っていると考えられる平面のことだ。接触平面が変化しないような曲線があるなら、その曲線はあるひとつの平面にのった曲線である。(たとえば円や直線なんかはそんな曲線である。) 図で表すと下のような感じ。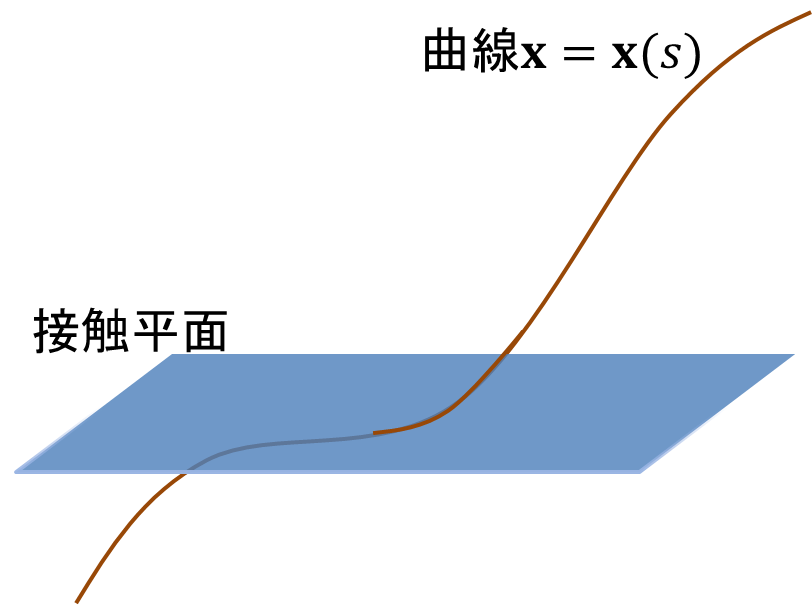
もしそんな曲面を見つけられれば、ある一点の近くではその曲線を平面の世界に落とし込んで考えることができるから、とても便利そうな感じがする。ということで求めていこう。
まず接触平面の性質としてまず間違いなく言えることは、その点での曲線の接線ベクトル\(\b{t}(s_0)=\b{x}'(s_0)\)に平行な平面であることだ。でも、もう一本接触平面が平行であるべきベクトルを見つけないと、平面の向きを定めることができない。もしもう一本見つけることができたなら、その2つのベクトルの外積を取ってやれば、平面の法線ベクトルがみつかり、したがって平面を定めることができる。
そこでこんな風に考える。\(s_0\)に十分近い点、\(s_0+\delta s\)をかんがえよう。接触平面というのだから、その2つの曲線上の点を結ぶベクトル\(\b{x}(s_0+\delta s) - \b{x}(s_0)\)がなるべくその平面上に乗っていて欲しい。もちろんこのベクトルの\(\delta s\)に対して一次の部分は接ベクトルそのものである。
接ベクトル\(\b{t} = \b{x}'(s_0)\)は当然接触平面に乗っていて欲しいはずだから、この二つのベクトルを用いて、接触平面の法線ベクトル\(\b{N}\)は、 \[\b{N} = \b{x}'(s_0)\times\left\{\b{x}(s_0+\delta s) - \b{x}(s_0)\right\}\] とかけると考える。ここで\(\b{x}(s_0+\delta s) - \b{x}(s_0) \) というベクトルをテイラー展開してやろう。すると、 \[\b{x}(s_0+\delta s) - \b{x}(s_0) = \b{x}'(s_0)\delta s + \frac{1}{2}\b{x}''(s_0) \delta s^2 + o(\delta s^3)\] というふうに展開される。これを代入すると、 \begin{align} \b{N} &= \b{x}'(s_0)\times\left\{\b{x}'(s_0)\delta s + \frac{1}{2}\b{x}''(s_0) \delta s^2 + o(\delta s^3)\right\}\\ &= \frac{1}{2}\b{x}'(s_0)\times\b{x}''(s_0) \delta s^2 + o(\delta s^3) \end{align} したがって、\(\delta s \to 0\)としたときに一番最後まで残っているのは、\(\frac{1}{2}\b{x}'(s_0)\times\b{x}''(s_0)\)である。...このベクトルは見覚えがある。前回紹介した従法線ベクトル\(\b{b}\)だ。
つまり、接触平面の法線ベクトルは、曲線の従法線ベクトルになる。
式でみるとたしかにそうだろうなあと思うかもしれないが、少し別の説明の仕方をしてみよう。要するに今回接触平面と平行であるべき、として採用したもう一本のベクトルは\(\b{x}''\)である。これは曲線の変化の2次の項までを、なるべく平面に乗せようと頑張りましょう、ということだ。
2.曲率・曲率半径
さて、ここからは曲率や曲率半径について話していく。曲率半径
とは、曲線の一部を円弧で近似したときの、その半径のことである。で、曲率
はその逆数のこと。これが分かれば、曲線の"曲がり具合"という抽象的な量を、統一的に表すことができる。なぜ先に接触平面というものについて説明したかといえば、その円が接触平面上にあるからだ。円というのはひとつの平面の上に乗った図形なのだから、当然一番よく近似したいなら接触平面上に円をのせるのがいい。考えるのは下の図のような近似だ。(円をただ1つに定めるには3点必要だから、3つの点で交わるように考える。)

目標は円の半径\(\rho\) (つまり曲率半径) を求めることだ。円の中心は\(\b{c}\)ということにしておこう。
そうすると、接触平面に乗った円の式は、その円上の点を示すベクトルを\(\b{p}\)として、次のような2つの方程式によって書くことができる。 \[\left\{\begin{align} |\b{p}-\b{c}|^2-\rho^2&= 0\\\\ \b{b}(s_1)\cdot(\b{p}-\b{x}(s_1))&=0 \end{align}\right.\tag{1}\] 二つ目の式は接触平面を表している。(点\(\b{x}(s_1)\)を通り、法線ベクトルとして\(s_1\)での曲線の従法線ベクトル\(\b{b}(s_1)\)を持つ平面。) この式に\(\b{p}=\b{x}(s_1),\b{x}(s_2),\b{x}(s_3)\)を代入して、極限を取りながら、\(\b{c}\)を消去できれば、半径を出すことができる。しかし力技でやるのはかなりめんどくさそうではないか。あんまりやりたくない。そこで、かなり技巧的にはなってしまうが、比較的簡単に出す方法があるので、それを使ってやってみよう。
もう一度確認だが、目標は曲線を近似する円の半径\(\rho\)を求めることだ。しかし、それをするには当然円の中心\(\b{c}\)を求めるのも避けては通れないだろう。そこでここからはまずは円の中心を決める方程式を導出してからすすめることにする。
B
ここでRolleの定理というのがあったのを思い出そう。Rolleの定理というのは、平均値の定理の特別版であり、 \[a< bに対して、f(a)=f(b) = 0 \Rightarrow f'(c)=0となるa< c< bが存在する。\] という定理であった。
じゃあこれを適用してみる。すると、\(f'(s_4)=0,~f'(s_5)=0\)となる\(s_1< s_4< s_2,~~s_2< s_5< s_3\)が存在するということが言える。
さらにもう一度適用すれば、\(f''(s_6)=0\)となる\(s_4< s_6< s_5\)が存在する。
今何をやっているのか思い出すと、曲線の一点のまわりを円で近似しようとしているのだった。そこで、全ての\(s_i\)を\(s_1\)に近づけて、極限をとってしまう。すると \[f'(s_1)=0,~~f''(s_1)=0\tag{3}\] がいえることが分かるだろう。すなわち、曲線を円で近似したとき、その点では(2)で定義した関数\(f(s)\)の2階微分までが消えているということだ。(3)式を具体的に計算すると、 \[\left\{\begin{align} \b{x}'(s_1)\cdot(\b{x}(s_1)-\b{c}) &= 0\\ \b{x}''(s_1)\cdot(\b{x}(s_1)-\b{c})+\b{x}'(s_1)\cdot\b{x}'(s_1) &=0 \end{align}\right.\tag{4}\] である。ところで、前回説明したように、\(\b{x}'\cdot\b{x}'=|\b{t}|^2=1\)また\(\b{x}''=\kappa\b{n}\)であった。(\(\b{t},\b{n}\)はそれぞれ曲線の接ベクトルと主法線ベクトル) これを代入して、 \[\left\{\begin{align} \b{t}(s_1)\cdot(\b{x}(s_1)-\b{c}) &= 0\\ \kappa\b{n}(s_1)\cdot(\b{x}(s_1)-\b{c})+1&=0 \end{align}\right.\tag{5}\] となる。これで円の中心\(\b{c}\)を求めるための方程式が2つ作れた。しかし、\(\b{c}\)は三次元の位置ベクトルなので、定めるためにはもう一つ方程式がいる。どうしようか。
実は最初に注意した「近似円は接触平面に乗るべき」という要求がもう一つの条件となる。円の中心も当然接触平面上にあるはずだから、(1)の接触平面の式から、 \[\b{b}(s_1)\cdot(\b{c}-\b{x}(s_1))=0\tag{6}\] が得られる。(5)の2つと(6)で3つの方程式ができたから、これで\(\b{c}\)を求められる。
さて、(5)の最初の式と(6)からわかることは、\(\b{c}-\b{x}(s_1)\)というベクトルは接ベクトル・従法線ベクトル\(\b{t},\b{b}\)どちらとも直交するということだ。この2つのベクトルと直交するということは、\(\b{c}-\b{x}(s_1)\)は主法線ベクトル\(\b{n}\)と同じ方向を向いているしかありえない。
\(\b{x}(s_1)\)というのは円上の一点を指しているから、当然\(\b{c}-\b{x}(s_1)\)の大きさはその円の半径\(\rho\)である。したがって、 \[\b{c}-\b{x}(s_1)=\rho\b{n}(s_1)\] を得る。あとはこれをまだ使っていなかった(5)の二番目の式に入れると、 \[\rho\kappa=1\Leftrightarrow\rho=\frac{1}{\kappa}=\frac{1}{\left|\frac{d^2\b{x}}{ds^2}\right|}\] と、ここで曲率半径が求まる。中心の座標はというと、 \[\b{c} = \b{x}(s_1) + \rho\b{n}(s_1)\] である。
実はFrenet-Serretの式の係数のうちのひとつ\(\kappa\)は、このようにして求めた円の半径の逆数そのもの、つまり曲線の曲がり具合を表す曲率そのものだったのだ。
3.色々な表し方
曲率の式は、 \[\kappa=\left|\frac{d^2\b{x}}{ds^2}\right|\tag{7}\] と求まった。しかし、普通の曲線が弧長\(s\)によってパラメータ表示されていることは少ないので、もっと一般的なパラメータ\(t\)で表された曲線\(\b{x}(t)\)の曲率を求める公式も作っておこう。まず、弧長\(s\)による微分は、次のようにパラメータ\(t\)による微分に変えられる。 \[\frac{d}{ds}=\frac{dt}{ds}\frac{d}{dt}\tag{8}\] そこで\(dt/ds\)がどのように表されるか考えよう。\(t\)が\(dt\)だけ変化したとき、対応する弧長\(ds\)は、 \[ds = \left|\frac{d\b{x}}{dt}\right|dt\tag{9}\] である。よって、 \[\frac{dt}{ds}=\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\tag{10}\] となり、(8)に代入して、 \[\frac{d\b{x}}{ds}=\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d\b{x}}{dt}\tag{11}\] を得る。もう一回(10)を使いながらsで微分すると、 \begin{align} \frac{d^2\b{x}}{ds^2}&=\frac{d}{ds}\frac{d\b{x}}{ds}\\ &=\frac{dt}{ds}\frac{d}{dt}\left(\frac{d\b{x}}{ds}\right)\\ &=\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d}{dt}\left(\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d\b{x}}{dt}\right)\tag{13} \end{align} \(\left|\frac{d\b{x}}{dt}\right|\)の微分が出てくるから、ここで、\(\b{x}(t)=(x(t),y(t),z(t))\)ということにして、具体的な計算をしてみる。 \[\frac{1}{\left|\frac{d\b{x}}{dt}\right|}=\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2\right)^{-1/2}\tag{14}\] なのでこれの微分は、 \begin{align} \frac{d}{dt}\frac{1}{\left|\frac{d\b{x}}{dt}\right|}&=\frac{d}{dt}\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2\right)^{-1/2}\\ &=-\frac{1}{2}\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2\right)^{-3/2}\frac{d}{dt}\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2\right)\\ &=-\left(\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2\right)^{-3/2}\left(\frac{dx}{dt}\frac{d^2x}{dt^2}+\frac{dy}{dt}\frac{d^2y}{dt^2}+\frac{dz}{dt}\frac{d^2z}{dt^2}\right) \end{align} となり、結局、 \[\frac{d}{dt}\frac{1}{\left|\frac{d\b{x}}{dt}\right|}=-\frac{1}{\left|\frac{d\b{x}}{dt}\right|^3}\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\] である。(14)の計算を進めていこう。 \begin{align} \frac{d^2\b{x}}{ds^2}&=\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d}{dt}\left(\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d\b{x}}{dt}\right)\\ &=\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\left[\frac{d}{dt}\left(\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\right)\frac{d\b{x}}{dt}+\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d^2\b{x}}{dt^2}\right]\\ &=\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\left[-\frac{1}{\left|\frac{d\b{x}}{dt}\right|^3}\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)\frac{d\b{x}}{dt}+\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d^2\b{x}}{dt^2}\right] \end{align} と、こうなる。最後にこのベクトルの大きさを求めれば曲率になる。 \begin{align} \left|\frac{d^2\b{x}}{ds^2}\right|^2&=\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left[-\frac{1}{\left|\frac{d\b{x}}{dt}\right|^3}\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)\frac{d\b{x}}{dt}+\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d^2\b{x}}{dt^2}\right]\cdot\left[-\frac{1}{\left|\frac{d\b{x}}{dt}\right|^3}\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)\frac{d\b{x}}{dt}+\frac{1}{\left|\frac{d\b{x}}{dt}\right|}\frac{d^2\b{x}}{dt^2}\right]\\ &=\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left[\frac{1}{\left|\frac{d\b{x}}{dt}\right|^4}\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)^2+\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left|\frac{d^2\b{x}}{dt^2}\right|^2-2\frac{1}{\left|\frac{d\b{x}}{dt}\right|^4}\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)^2\right]\\ &=\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left[\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left|\frac{d^2\b{x}}{dt^2}\right|^2-\frac{1}{\left|\frac{d\b{x}}{dt}\right|^4}\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)^2\right]\\ \end{align} つまり、 \[\left|\frac{d^2\b{x}}{ds^2}\right|=\frac{1}{\left|\frac{d\b{x}}{dt}\right|^3}\sqrt{\left|\frac{d\b{x}}{dt}\right|^2\left|\frac{d^2\b{x}}{dt^2}\right|^2-\left(\frac{d\b{x}}{dt}\cdot\frac{d^2\b{x}}{dt^2}\right)^2}\tag{15}\] これが曲率の計算公式である。これで終わりでもいいんだけど、もう少しだけ計算してみた。
(15)の括弧の中をみると、\(\frac{d\b{x}}{dt},\frac{d^2\b{x}}{dt^2}\)のなす角度\(\theta\)を使うと簡単になりそうな気がする。具体的にやってみると、 \begin{align} \left|\frac{d^2\b{x}}{ds^2}\right|&=\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left|\frac{d^2\b{x}}{dt^2}\right|\sqrt{1-\cos^2\theta}\\ &=\frac{1}{\left|\frac{d\b{x}}{dt}\right|^2}\left|\frac{d^2\b{x}}{dt^2}\right||\sin\theta| \end{align} \(\sin\theta\)といえば外積だ。 \[\left|\frac{d\b{x}}{dt}\times\frac{d^2\b{x}}{dt^2}\right|=\left|\frac{d^2\b{x}}{dt^2}\right|\left|\frac{d\b{x}}{dt}\right|\left|\sin\theta\right|\] だから、 \[\left|\frac{d^2\b{x}}{ds^2}\right| = \left|\frac{d\b{x}}{dt}\times\frac{d^2\b{x}}{dt^2}\right|/\left|\frac{d\b{x}}{dt}\right|^3\] ともかけることが分かった。この形まで持ってきたほうが、多分計算は楽だし、弧長sをパラメータとして使ったときに元に戻るのがわかりやすい。