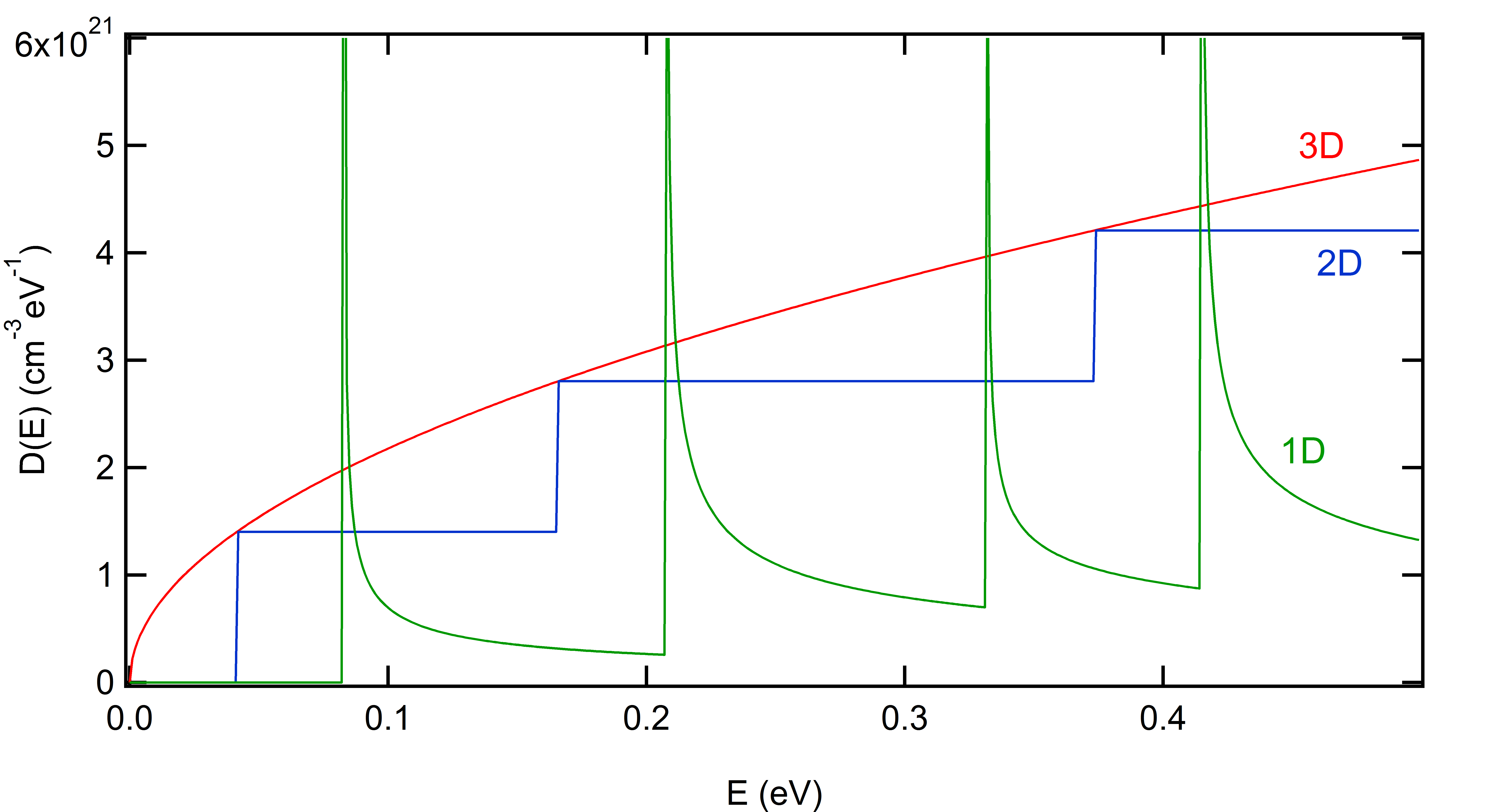
一次元・二次元自由電子の状態密度
1.低次元電子
最近の成膜技術や微細加工技術はとんでもなく高度なものになっていて、電子を平面に閉じ込めたり、線に閉じ込めたり、さらには点で閉じ込めたりできる技術がある。こういう低次元に閉じ込められた電子は、それまで知られていたバルク(普通のかたまり)材料とは全く違う性質を示す。今回はこういう電子の状態密度を調べて、どのような状況になっているかを計算してみよう。
2.二次元自由電子
二次元自由電子とは、ある軸方向にはとっても小さな幅\(L\)で閉じ込められ、それ以外の方向には自由に動き回れるような電子の状態のことだ。こういうのは量子井戸
と呼ばれるが、現実の世界でもnmオーダーの薄膜を作ることで実現されている。閉じ込められている方向はz軸方向だとしよう。z軸には閉じ込められていて、xy平面方向には自由に動き回れる電子のエネルギー状態は以下のようになる。 \[E(\b{k}) = \frac{\hbar^2}{2m}(k_x^2+k_y^2)+\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)\tag{1}\] xy平面には自由に動き回れるので、xy平面方向の波数\(k_x,k_y\)はほとんど連続的に変化するが、z方向には閉じ込められているので、波数が\(k_z=n^2\pi^2/L\)(n=1,2,3,...)に離散化される。
で、状態密度はといえば、デルタ関数の和として表されて \[D(\epsilon)=\frac{2}{V}\sum_\b{k}\delta(\epsilon - E(\b{k}))\tag{2}\] だから、積分に直しながら計算してみよう。ただし、積分に直せるのは波数が連続的に変化するとみなせるxy方向についてだけである。 \begin{align} D(\epsilon)&=\frac{2}{V}\sum_\b{k}\delta(\epsilon - E(\b{k})) \\ &= \frac{2}{(2\pi)^2}\sum_n\int \delta(\epsilon - E(\b{k})) dk_xdk_y \\ &= \frac{2}{(2\pi)^2}\sum_n\int \delta\left(\epsilon - \frac{\hbar^2}{2m}(k_x^2+k_y^2)-\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)\right) dk_xdk_y \end{align} このままだと積分の計算が難しそうだから、まずは円柱座標に移ろう。 \[ D(\epsilon) = \frac{1}{\pi}\sum_n\int_0^\infty \delta\left(\epsilon - \frac{\hbar^2k^2}{2m}-\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)\right) k ~dk \\ \] さらに\(s= \frac{\hbar^2k^2}{2m}+\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)-\epsilon\)と変数変換する。すると、 \begin{align} D(\epsilon) &= \frac{1}{\pi}\frac{m}{\hbar^2}\sum_n\int_{\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)-\epsilon}^\infty \delta\left(s\right) ds \\ \end{align} さて、デルタ関数を積分すると、積分範囲に0を含むとき1で、それ以外では積分は0になるのだった。つまり、 \[ \int_{\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)-\epsilon}^\infty \delta\left(s\right) ds = \left\{\begin{array}{cc} 0&\left(\text{if}~~~\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)-\epsilon\gt 0\right)\\ 1&\left(\text{if}~~~\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)-\epsilon\lt 0\right) \end{array}\right. \] こういう階段状に変化する関数は、ステップ関数というのがあった。 \[H(x)= \left\{\begin{array}{cc} 1&\left(\text{if}~~~x\gt 0\right)\\ 0&\left(\text{if}~~~x\lt 0\right) \end{array}\right. \] だから、これを使うと、 \[ \int_{\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)-\epsilon}^\infty \delta\left(s\right) ds = H\left(\epsilon-\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)\right)\] とできる。したがって状態密度は \[D(\epsilon)= \frac{m}{\pi\hbar^2}\sum_{n=1}^\infty H\left(\epsilon-\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)\right)\tag{3} \] となる。ページの最後にグラフを載せた。
3.一次元自由電子
xy方向に幅\(L\)で閉じ込められた電子を考えよう。こういうのは量子細線
とも呼ばれる。最近話題のカーボンナノチューブもそうだし、最近では、SiやGaAsといった半導体のナノワイヤも作れるようになってきている。このときのエネルギー状態は、xy方向に離散化されて \[E(\b{k}) = \frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)+\frac{\hbar^2k_z^2}{2m}\tag{4}\] となる。状態密度を求めよう。この場合、連続的に変化する変数は\(k_z\)だけだから、積分として取り扱えるのはz方向だけである。 \begin{align} D(\epsilon)&=\frac{2}{V}\sum_\b{k}\delta(\epsilon - E(\b{k})) \\ &=\frac{2}{2\pi}\sum_{n_x,n_y}\int_{-\infty}^\infty \delta\left(\epsilon - \frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)-\frac{\hbar^2k_z^2}{2m}\right) dk_z \\ &=\frac{1}{\pi}\sum_{n_x,n_y}\int_{\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)}^\infty \delta\left(\epsilon -s\right) \sqrt{\frac{m}{2\hbar^2\left(s-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)\right)}}ds ~~~~~\left(s= \frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)+\frac{\hbar^2k_z^2}{2m}\right)\\ &=\frac{1}{\pi}\sqrt{\frac{m}{2\hbar^2}}\sum_{n_x,n_y}\int_{\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)}^\infty \delta\left(\epsilon -s\right) \left(s-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)\right)^{-1/2}ds\\ \end{align} さっきと同じように考えると、上の積分は次のようになる。 \[ \int_{\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)}^\infty \delta\left(\epsilon -s\right) \left(s-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)\right)^{-1/2}ds = \left\{\begin{array}{cc} 0&\left(\text{if}~~~\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)-\epsilon\gt 0\right)\\ \left(\epsilon-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)\right)^{-1/2}&\left(\text{if}~~~\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)-\epsilon\lt 0\right) \end{array}\right. \] ということで、さっきと同じようにステップ関数を使うと、 \[D(\epsilon)=\frac{1}{\pi}\sqrt{\frac{m}{2\hbar^2}}\sum_{n_x,n_y=1}^\infty \frac{1}{\sqrt{\epsilon-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)}}H\left(\epsilon-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)\right)\] となる。
4.自由電子の状態密度 (1,2,3次元)
今回は導出しなかったが、三次元の状態密度も合わせて書いておく。それぞれ\(D_3,D_2,D_1\)とすると、 \begin{align} D_3(\epsilon)&=\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\sqrt{\epsilon}\\\\ D_2(\epsilon)&=\frac{m}{\pi\hbar^2}\sum_{n=1}^\infty H\left(\epsilon-\frac{\hbar^2}{2m}\left(\frac{n^2\pi^2}{L^2}\right)\right)\\\\ D_1(\epsilon)&=\frac{1}{\pi}\sqrt{\frac{m}{2\hbar^2}}\sum_{n_x,n_y=1}^\infty \frac{1}{\sqrt{\epsilon-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)}}H\left(\epsilon-\frac{\hbar^2}{2m}\left(\frac{\pi^2}{L^2}\right)(n_x^2+n_y^2)\right) \end{align} となっている。どんな感じかグラフを書いておこう。質量は普通の自由電子の質量、閉じ込めの大きさは3 nm した。一次元電子には状態密度が発散する点が幾つかあるが、こういう点は
Van Hove特異点
と呼ばれたりもする。