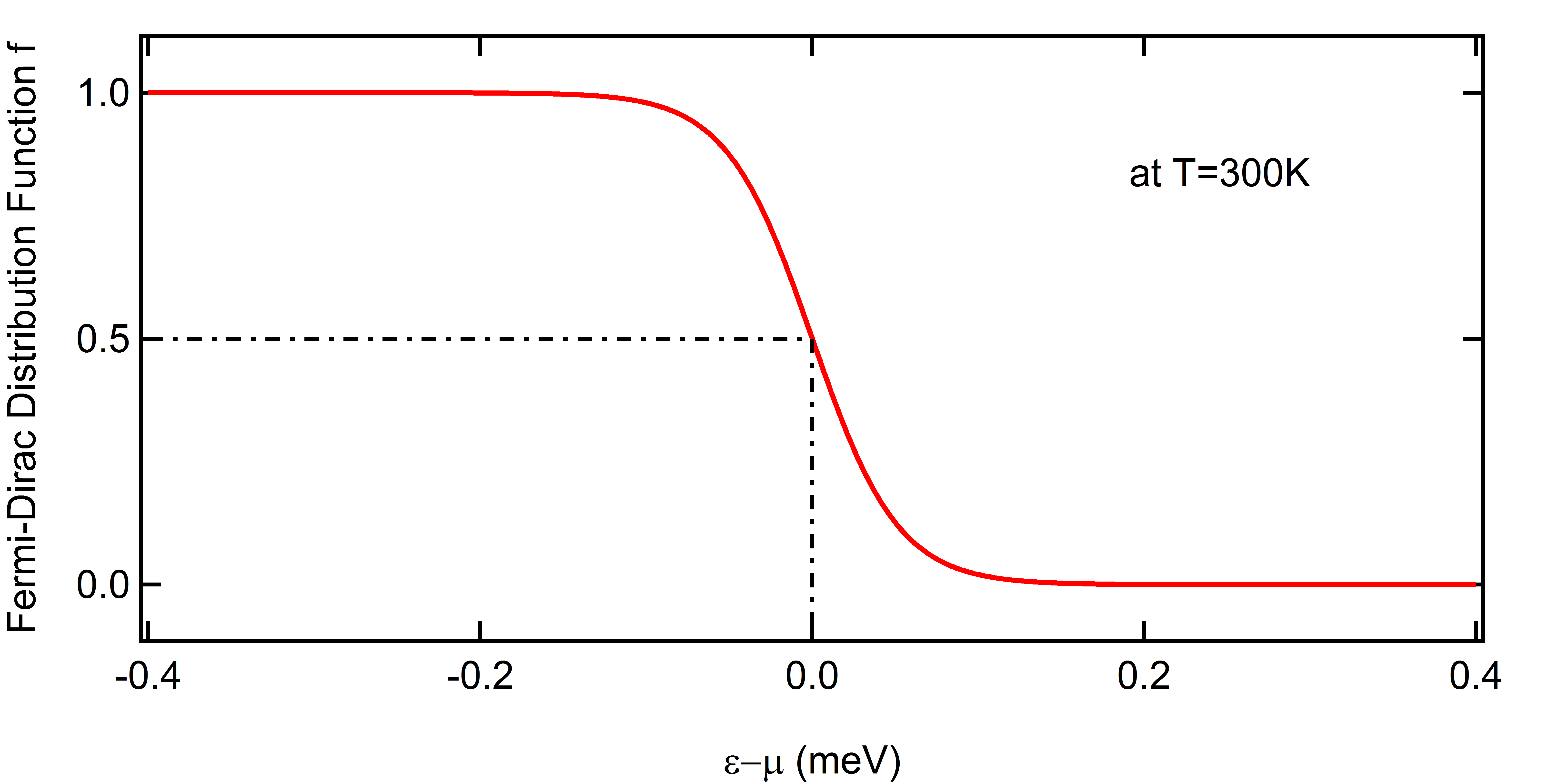
1.自由電子
自由電子とは、エネルギーが波数の2乗に比例する形、つまり
\[E_k = \frac{\hbar^2k^2}{2m}\tag{1}\]
で書かれるような電子のことだ。金属中の電子なんかは、結構良い近似で(1)の形にかける。そこで今回は、この自由電子が持つ比熱を紹介しようと思う。金属の低温比熱は、自由電子のモデルによってかなり良く説明されるのだ。結果を先に書いておくと、
\[C(T) \approx \frac{1}{4}\left(\frac{2m}{\hbar^2}\right)^{3/2}\mu^{1/2}k^2 T\]
となり、低温では比熱が温度に比例することが示される。\(\mu\)はフェルミレベルである。
比熱を調べるには、状態密度を知っておく必要がある。そこで最初に自由電子の状態密度を書いておくと、
この前導出したとおり、
\[D(E)dE = \frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\sqrt{E}dE\tag{4}\]
である。
なぜ比熱なんかを考えるのかというと、それは実験的に測定できるのが内部エネルギーなんかではなく、比熱という量だからだ。物質の内部エネルギーがどれだけあるかなんて言うことは、誰も測定することができないだろう。しかし、どれだけの熱量を与えてどれだけの温度上昇があるか、ということは測定可能だ。もし金属の比熱がこの自由電子モデルによってよく説明できるのであれば、それは金属中の電子が自由電子的に振る舞っている間接的な証拠になるだろう。
2.比熱を計算するためには
比熱とは、単位量の物質の温度を1K上昇させるのに必要なエネルギーのことである。具体的に式で書くなら、温度\(T\)における比熱は、温度\(T\)において単位量の物質が持つエネルギー\(E(T)\)をつかって、
\[c(T) = \frac{dE}{dT}\tag{3}\]
である。つまり自由電子のエネルギーと状態密度、それにフェルミ分布関数
\[f(E) = \frac{1}{1+\exp\left(\frac{E-\mu}{kT}\right)}\tag{4}\]
を使って、ある温度におけるエネルギー\(E(T)\)を求められれば、それを微分することによって比熱を求められるわけだ。
ということで、ここからはエネルギーを求めていこう。エネルギー\(\epsilon\)から\(\epsilon+d\epsilon\)の間にいる電子の数は、
\[f(\epsilon)D(\epsilon)d\epsilon\tag{5}\]
だから、全体のエネルギーは、これにエネルギーを掛けて積分すればいい。よって、
\[E = \int\epsilon f(\epsilon)D(\epsilon)d\epsilon\tag{6}\]
が今回計算するべき量である。
3.計算
じゃあ(6)を計算していこう。まずは状態密度と分布関数を代入して、
\[E = \frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\int_0^\infty\frac{\epsilon^{3/2}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\tag{6}\]
となる。だから、
\[\int_0^\infty\frac{\epsilon^{3/2}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\tag{7}\]
という積分が計算できればいいわけだ。この積分を計算するにはどうしたらいいだろうか。うまいこと変数変換すればできたりするかな。と思ったりしてしまうが、実はこの積分は
フェルミ積分
と呼ばれていて、普通の関数では表せないことが知られている。数値計算をすれば任意の温度について計算できないことも無いのだが、しかしそれでは実験との比較がしにくい。
じゃあどうするのかというと、低温である (\(T\approx 0\)) という条件をつけて、近似的な表式を見つけ出してやるのだ。そこでまずは、絶対零度付近において分布関数
\[f(\epsilon) = \frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}\]
がどのように振る舞うか考えてみよう。
フェルミ分布関数は、以下のような形をしていた。
実はこの関数を\(\epsilon\)で微分した、
\begin{align}
\frac{df}{d\epsilon} &= \frac{1}{kT}\frac{\exp\left(\frac{\epsilon-\mu}{kT}\right)}{\left(1+\exp\left(\frac{\epsilon-\mu}{kT}\right)\right)^2}\\
&=\frac{1}{2kT}\frac{1}{1+\cosh\left(\frac{\epsilon-\mu}{kT}\right)}
\end{align}
という関数が、\(\epsilon=\mu\)の付近(大体\(kT\)の幅)以外ではほとんど0になってしまうという性質を使うと、うまいこと計算を進められる。分布関数を微分した関数を登場させてやれば、この小さい幅だけを積分すれば良くなるからだ。この関数のグラフを下に示しておこう。
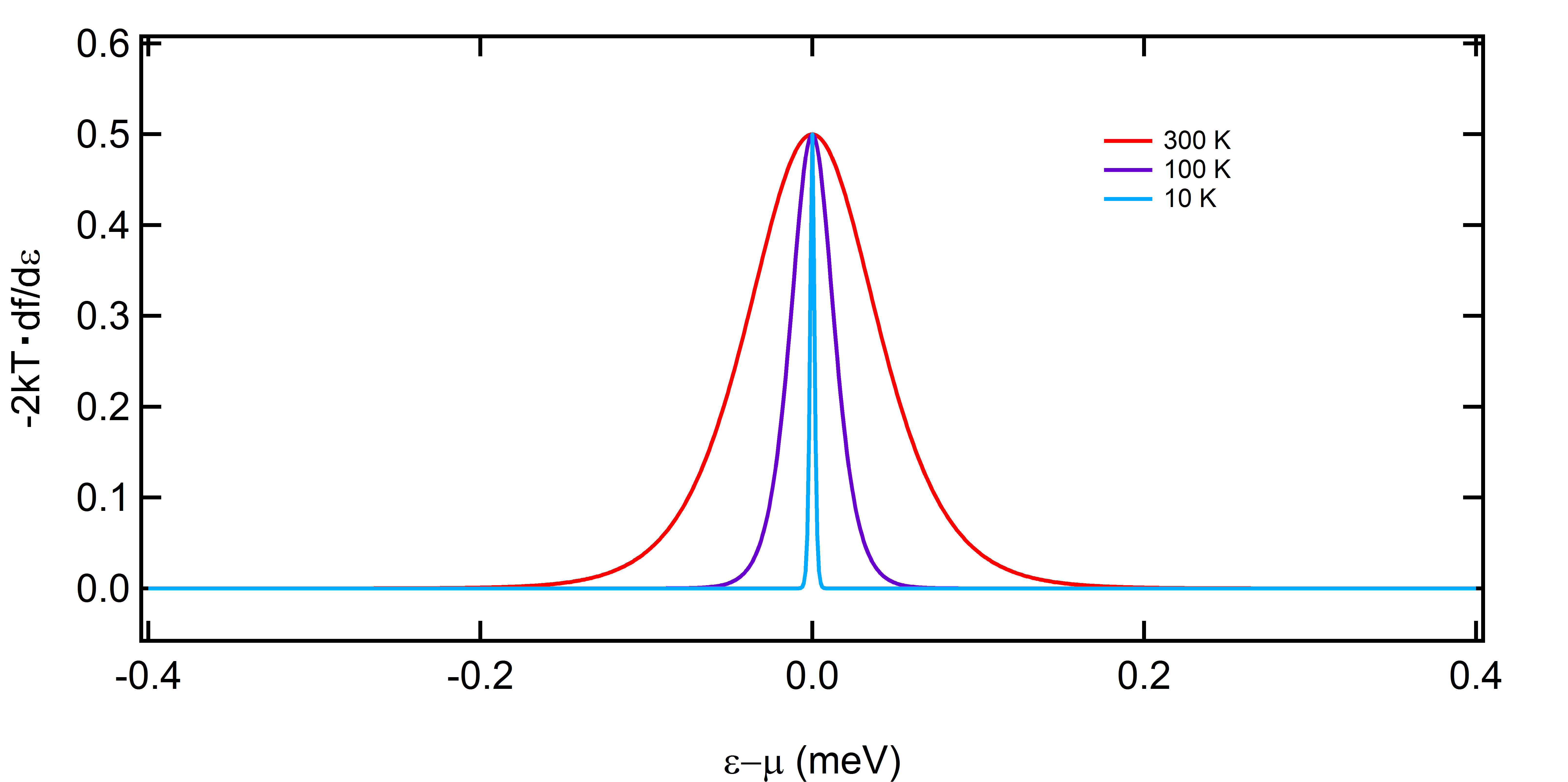
で、じゃあこの関数をどうやって登場させるのかというと、(7)を部分積分すればいい。やってみると、
\begin{align}
&\int_0^\infty\frac{\epsilon^{3/2}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\
&=\left[\frac{2}{5}\epsilon^{5/2}\frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}\right]_o^\infty-\frac{2}{5}\int_0^\infty\epsilon^{5/2}\frac{d}{d\epsilon}\frac{1}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\\\
&=\frac{1}{5kT}\int_0^\infty\frac{\epsilon^{5/2}}{1+\cosh\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\
\end{align}
が得られる。この積分を評価するために、\(1/1+\cosh\left(\frac{\epsilon-\mu}{kT}\right)\)が\(\epsilon=\mu\)の付近以外ではほとんど0になることを念頭に置いて、\(\epsilon^{5/2}\)を\(\epsilon=\mu\)のまわりでテイラー展開してみよう。
\begin{align}
\epsilon^{5/2} &= \mu^{5/2} + \frac{5}{2}\mu^{3/2}(\epsilon-\mu)+\frac{1}{2!}\frac{5}{2}\frac{3}{2}\mu^{1/2}(\epsilon-\mu)^2+\cdots\\
&=\mu^{5/2} + \frac{5}{2}\mu^{3/2}(\epsilon-\mu)+\frac{15}{8}\mu^{1/2}(\epsilon-\mu)^2+\cdots
\end{align}
これを代入すると、
\begin{align}
&\int_0^\infty\frac{\epsilon^{3/2}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\
&=\frac{1}{5kT}\int_0^\infty\frac{1}{1+\cosh\left(\frac{\epsilon-\mu}{kT}\right)}\left(\mu^{5/2}+\frac{5}{2}\mu^{3/2}(\epsilon-\mu)+\frac{15}{8}\mu^{1/2}(\epsilon-\mu)^2+\cdots\right)d\epsilon\\
\end{align}
さて、ここで\((\epsilon-\mu)/kT = x\)と変数変換する。すると、
\begin{align}
&=\frac{1}{5}\int_{-\mu/kT}^\infty\frac{1}{1+\cosh\left(x\right)}\left(\mu^{5/2}+\frac{5}{2}\mu^{3/2}kTx+\frac{15}{8}\mu^{1/2}(kT)^2x^2+\cdots\right)dx\\
\end{align}
を得る。積分範囲が\(-\mu/kT\to\infty\)となっているが、今は低温の場合を考えているのだった。そこでフェルミレベル\(\mu\)が熱エネルギー\(kT\)よりも十分大きいと仮定すると、この積分は\(-\infty\to\infty\)と考えてもほとんど問題ないだろう。そうすると、
\begin{align}
&\approx\frac{1}{5}\int_{-\infty}^\infty\frac{1}{1+\cosh\left(x\right)}\left(\mu^{5/2}+\frac{5}{2}\mu^{3/2}kTx+\frac{15}{8}\mu^{1/2}(kT)^2x^2+\cdots\right)dx\\
\end{align}
となる。ということで、問題になるのは、
\[I_n = \int_{-\infty}^\infty\frac{x^n}{1+\cosh\left(x\right)}\]
という積分である。\(n\)が奇数のときには明らかに奇関数で0になるが、この積分をしっかりと計算するのは結構難しい。そこで、
wolframalphaさんに聞いて結果だけ拝借しよう。\(n=1\)は消えてしまうので、最低次の項である\(n=0,2\)の場合には、
\[I_0 = \int_{-\infty}^\infty\frac{1}{1+\cosh\left(x\right)} = 2\]
\[I_2 = \int_{-\infty}^\infty\frac{x^2}{1+\cosh\left(x\right)} = \frac{2\pi^2}{3}\]
となるそうだ。代入すると、
\begin{align}
&\int_0^\infty\frac{\epsilon^{3/2}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\
&\approx\frac{2}{5}\mu^{5/2}+\frac{\pi^2}{4}\mu^{1/2}(kT)^2+o(T^4)
\end{align}
が得られる。
よって求めたかったエネルギーの式に代入すると、
\begin{align}
E(T) &= \int\epsilon f(\epsilon)D(\epsilon)d\epsilon \\
&= \frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\int_0^\infty\frac{\epsilon^{3/2}}{1+\exp\left(\frac{\epsilon-\mu}{kT}\right)}d\epsilon\\
&\approx\frac{1}{2\pi^2}\left(\frac{2m}{\hbar^2}\right)^{3/2}\left(\frac{2}{5}\mu^{5/2}+\frac{\pi^2}{4}\mu^{1/2}(kT)^2+o(T^4)\right)\\
\end{align}
第一項目は絶対零度のときのエネルギーを表すから、\(E(0)\)と書いてしまうと、
\[E(T) \approx E(0) + \frac{1}{8}\left(\frac{2m}{\hbar^2}\right)^{3/2}\mu^{1/2}(kT)^2+o(T^4)\tag{8}\]
となる。
何をしたかったのかというと、比熱を求めたかったのだった。そこでこれを\(T\)で微分して、
\[C(T) \approx \frac{1}{4}\left(\frac{2m}{\hbar^2}\right)^{3/2}\mu^{1/2}k^2 T\]
が求める比熱である。
今回用いた計算手法は、一般に
ゾンマーフェルト展開
と呼ばれる手法である。そのうち別個で説明ページを作るかもしれないし、作らないかもしれない。