ファンデルワールス力の導出・ファンデルワールス結合
1.ファンデルワールス力とは
ファンデルワールス力
とは、基本的にどんな分子の間にも働く力のことで、電荷のゆらぎを起源としている。その電荷のゆらぎ同士が引き合うことで、力を発生させるのだ。分子間力と呼ばれることもあるようだ。二酸化炭素なんかはこの力で凝集してドライアイスとなる。しかしこの力、ゆらぎを起源としているだけあって、かなり弱い。電気力なんかがあれば、たちまちその影に隠れてしまう。だから、大きな電気力の影響を受けにくい、希ガス原子や無極性分子の結合に強く関連してくる。
実は、熱力学のファンデルワールス気体のところでも出てくるのだが、熱力学では細かいところには立ち入らずにpVTの状態方程式だけ導出して終わった。ということで、今回は物理的に、ファンデルワールス力の性質を考えていく。
2.ファンデルワールス力の導出
かなり長くなるが、頑張って書いてみた。ちょっとばかり数式のレンダリングに時間がかかると思う。図のように、ある希ガス原子の電荷が少しだけ偏って存在していて、原子内の電荷はバネのような復元力でもって繋がれているとする。本当は電荷が連続的に分布しているようになっているはずだが、簡単のために点電荷\(\pm q\)があることにしよう。実際には原子内の電荷同士はバネなんかではなく、電気力で引き合ってその大きさを維持しているのだが、今回はめんどくさいのでバネにその役目を任せてしまおうというところだ。(点電荷を使って原子内の電荷を議論しようとすると原子の大きさがゼロになってしまったりして色々と大変。)
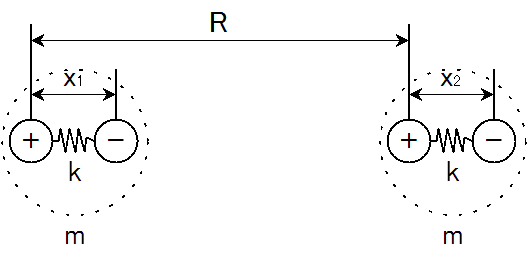
まあニュートンの運動方程式から解くのは無謀だろうから、解析力学の力を借りて、ハミルトニアンを使った正準方程式(下の式)で解くことにする。 \[\left\{\begin{align} \frac{dp_i}{dt}&=\frac{\partial H}{\partial x_i} \\\\ \frac{dx_i}{dt}&=-\frac{\partial H}{\partial p_i} \end{align}\right.\] ハミルトニアンは、系の全エネルギーを求めればよい。まず運動エネルギー\(K\)は、 \[K=\frac{1}{2}m\ddot{x}_1^2+\frac{1}{2}m\ddot{x}_2^2=\frac{p_1^2}{2m}+\frac{p_2^2}{2m} \tag{1}\] である。復元力による弾性エネルギー\(U_1\)は、 \[U_1=\frac{1}{2}kx_1^2+\frac{1}{2}kx_2^2 \tag{2}\] となる。さらに静電気力によるエネルギー\(U_2\)は \[U_2=q^2\left(\frac{1}{R} + \frac{1}{R-x_1+x_2} - \frac{1}{R-x_1} - \frac{1}{R+x_2}\right)\] となる。わかるだろうか?今回は一つの原子内の電荷同士の静電気力をバネに預けてしまったからこういう形になる。とまあここまでは簡単。
ここで原子の大きさに比べて、原子間の距離が十分大きいと仮定しよう。すると、 \[\begin{align} U_2 &= \frac{q^2}{R}\left(1+\frac{1}{1+\frac{x_2-x_1}{R}}-\frac{1}{1-\frac{x_1}{R}}-\frac{1}{1+\frac{x_2}{R}}\right)\\\\ &\approx \frac{q^2}{R}\left\{1+\left(1-\frac{x_2-x_1}{R}+\left(\frac{x_2-x_1}{R}\right)^2\right)- \left(1+\frac{x_1}{R}+\frac{x_1^2}{R^2}\right)-\left(1-\frac{x_2}{R}+\frac{x_2^2}{R^2}\right)\right\} \\\\ &= -\frac{2q^2}{R^3}x_1x_2 \tag{3}\end{align} \] 途中の近似には、\(1/(1+x)\approx 1 - x + x^2\)を用いた。ちょっとめんどくさい計算だが、しっかりやれば\(U_2\)を簡単な形に近似することができた。
(1), (2), (3)式を用いて、全エネルギー、すなわちハミルトニアンは、 \[\begin{align} H&= K + U_1+U_2 \\ &= \frac{p_1^2}{2m}+\frac{p_2^2}{2m} + \frac{1}{2}kx_1^2+\frac{1}{2}kx_2^2 -\frac{2q^2}{R^3}x_1x_2 \tag{4} \end{align}\] となる。では(4)を正準方程式に入れてしまおう。すると、運動量で微分する方では、 \[ \dot{x}_1=\frac{p_1}{m} \] という式も出てくるが、これは当たり前の式なので気にしないでいい。重要なのは\(x_i\)で微分するほうだ。それを計算すると、 \[\left\{\begin{align} \dot{p}_1 = kx_1-\frac{2q^2}{R^3}x_2 \\\\ \dot{p}_2 = kx_2-\frac{2q^2}{R^3}x_1 \end{align}\right.\] さて、どうやって解こう。まずは運動量を位置の微分で表しておく。(\(p=m\dot{x}\)を使って) \[\left\{\begin{align} m\ddot{x}_1 = kx_1-\frac{2q^2}{R^3}x_2 \\\\ m\ddot{x}_2 = kx_2-\frac{2q^2}{R^3}x_1 \end{align}\right.\] それで両辺を足すのと引くのとしてみる。すると、 \[\left\{\begin{align} m(\ddot{x}_1+\ddot{x}_2) = \left(k-\frac{2q^2}{R^3}\right)(x_1+x_2) \\\\ m(\ddot{x}_1-\ddot{x}_2)= \left(k+\frac{2q^2}{R^3}\right)(x_1-x_2) \end{align}\right.\] を得る。これなら解けるぞ。\(y_1\equiv x_1+x_2\),\(y_2\equiv x_1-x_2\)とみればこれは単振動の方程式じゃないか。
ということで、解として、 \[ \left\{\begin{align} y_1 &= A_1e^{i\omega_1 t} + B_1e^{-i\omega_1 t} \\ y_2 &= A_2e^{i\omega_2 t} + B_2e^{i\omega_2 t} \end{align}\right. \tag{5} ただし、\omega_1= \sqrt{\frac{1}{m}\left(k-\frac{2q^2}{R^3}\right)}, ~~ \omega_2= \sqrt{\frac{1}{m}\left(k+\frac{2q^2}{R^3}\right)} \] が得られる。\(x_1, x_2\)の解が知りたければ、足したり引いたり2で割ったりすればよいのはわかるだろう。
で、肝心のファンデルワールス力は?ということで、この系のエネルギーを考えてみる。量子論的な考え方を思い出すが、量子力学的な調和振動子のエネルギーEは、整数nを使って、 \[ E_n = \left(n+\frac{1}{2}\right)\hbar\omega \] で与えられるのだった。ということは、n=0(基底状態)で今回の系のエネルギーは、2つの振動状態が同時に存在しているとすれば、 \[ E_0 = \frac{1}{2}(\omega_1 + \omega_2) \tag{6} \] となる。で、これを計算するために、\(\omega_1, \omega_2\)をテイラー展開してしまおう。kというのは原子の中で働いている力の大きさを表していて、\(2q^2/R^3\)という項は僅かな電荷の偏りによって、原子同士がクーロン力で引き合っている力を表している。だから\(2q^2/R^3\ll k\)が成り立っているとしても問題無い。よって、 \(\sqrt{1+x}\approx 1+x/2-x^2/8\)を用いれば、 \[\begin{align} \sqrt{\frac{1}{m}\left(k\pm\frac{2q^2}{R^3}\right)} &= \sqrt{\frac{k}{m}}\sqrt{1 \pm \frac{2q^2}{kR^3}} \\\\ &\approx \sqrt{\frac{k}{m}} \left (1\pm \frac{q^2}{kR^3} - \frac{1}{8}\left(\frac{2q^2}{kR^3}\right)^2\right) \end{align}\] これによって(6)式を計算すると、下の結果が出る! \[ \begin{align} E_0 &= \sqrt{\frac{k}{m}} \left(1 - \frac{1}{8}\left(\frac{2q^2}{kR^3}\right)^2\right) \\\\ &= \omega_0 \left(1-\frac{A}{R^6}\right)\tag{6} \end{align}\] ただし\(\omega_0=\sqrt{k}{m}, A=2q^2/8k\)とした。
さて、この結果(6)式から、ファンデルワールス力が働くというのだが、わかるだろうか。物質というのは、いつでも持っているエネルギーを出来るだけ小さくしたい。(6)式をみると、原子間距離Rが小さくなれば、系のエネルギーも小さくなることがわかる。つまり、(6)式こそがファンデルワールス力の起源なのだ!
ところで、力に寄与する部分\(A/R^6\)の係数は\(A=2q^2/8k\)で非常に小さい。このことから、ファンデルワールス力がいかに小さい力か理解できるだろう。また、力の大きさは一般にエネルギーの微分で表せることに注意すれば、ファンデルワールス力の大きさは大体\(R^{-7}\)に比例すると考えられる。電磁気力は\(R^{-2}\)に比例するから、電磁気力と比べると相当近くの原子同士でしか作用しないのだ。これも実際の自然現象にあっているから、だいたい良い感じで導出できたといえるんじゃないだろうか?