物理とか

Index

作用変数と振動数(交換関係導出の補足)

[prev:交換関係の発見とハイゼンベルクの行列力学] [index] [next:ハイゼンベルクの行列力学の導出]

1.一般の場合の対応原理

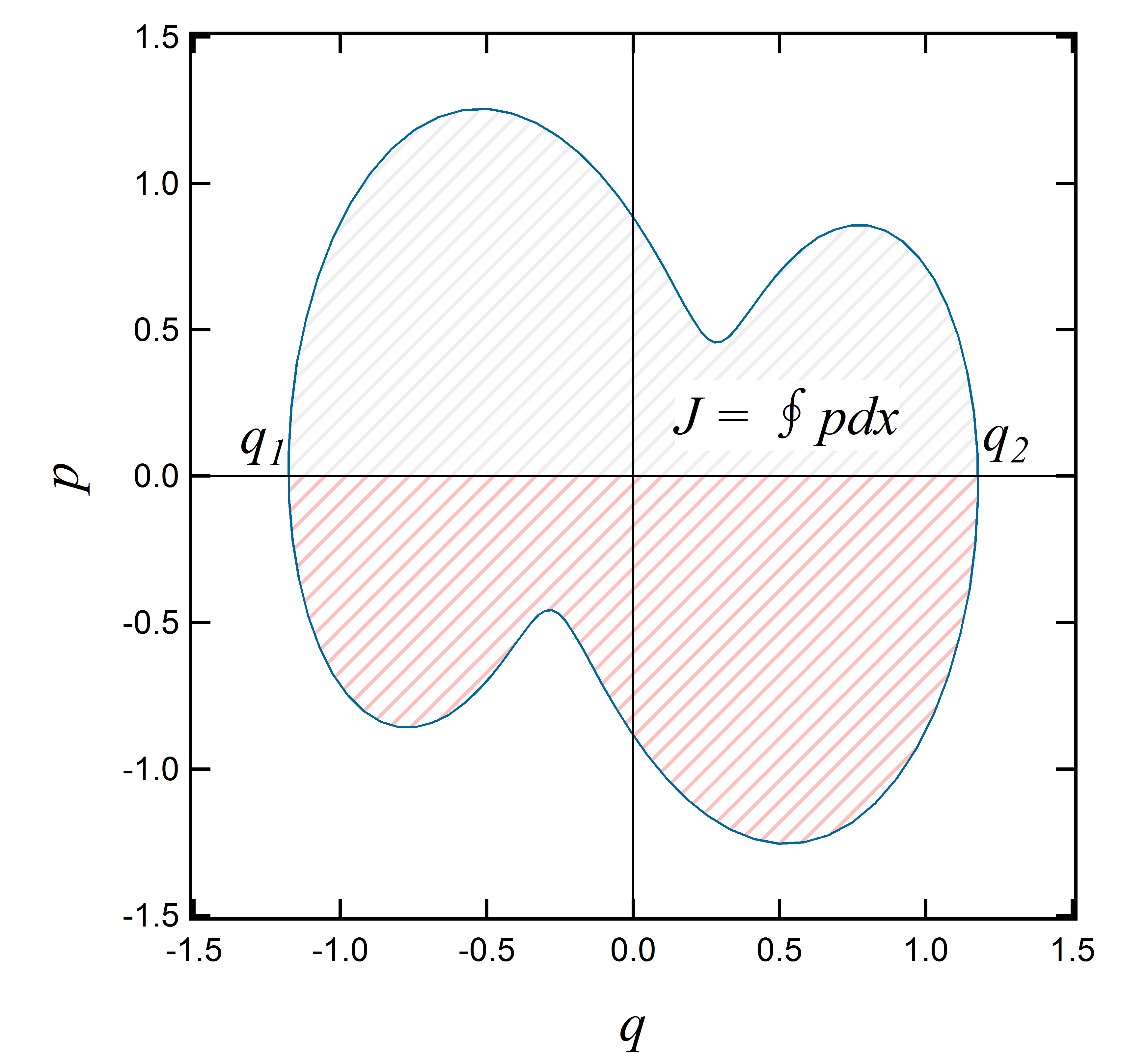
[原子の構造・水素原子スペクトルとボーアの原子模型]では水素原子の場合について、エネルギーが大きいときに古典理論と量子論の対応原理が成立することを示したが、今回は一般の周期運動の場合についてみてみよう。

量子条件で主役となる作用変数は \[J=\oint pdq\] という量だった。今回は簡単のために一次元の場合を考えることにすると、実は、この作用変数とエネルギー\(E\)を用いて周期\(T\)は \[\tag{1}T=\frac{dJ}{dE}\] と書けるのだ。これを証明してみよう。まず、\(J\)を\(p\)が0以上となる範囲と0以下になる\(q\)の範囲を使って次のように書き直そう。書き直すというか、積分範囲をしっかりと示すだけだ。下には今考えている概念図を書いておいた。 \[J=J_+ + J_- = \int_{q_1}^{q_2} p_+ dq+\int_{q_2}^{q_1} p_- dx\tag{2}\]

こういうふうにしておいて、(1)を導出したいからエネルギーで微分しよう。+側と-側は全く同じように計算できるから、＋側だけ考えれば十分だ。 \begin{align} \frac{dJ_+}{dE} &= \frac{d}{dE}\int_{q_1}^{q_2} p_+ dq \\ &= \int_{q_1}^{q_2} \frac{\partial p_+}{\partial E} dq \\ &= \int_{q_1}^{q_2} \frac{1}{\frac{\partial E}{\partial p_+}} dq \end{align} さらにエネルギーは一般に(孤立系では)ハミルトニアン\(H(p,q)\)に等しいから、 \[\frac{dJ_+}{dE} = \int_{q_1}^{q_2} \frac{1}{\frac{\partial H}{\partial p_+}} dq\] ハミルトン形式の運動方程式から、 \[\frac{dq}{dt}=\frac{\partial H}{\partial p_+}\] なので、 \begin{align} \frac{dJ_+}{dE} &= \int_{q_1}^{q_2} \frac{1}{\frac{dq}{dt}} dq\\ &=\int_{t_1}^{t_2} dt\\ &=T_+ \end{align} ただし\(T_+\)というのは+側を軌道が通るのにかかる時間である。-側も全く同じように計算できて、これで \[T=\frac{dJ}{dE}\tag{1}\] が証明できた。さらに振動数\(\nu=1/T\)は \[\nu=\frac{dE}{dJ} \tag{3}\] となることがわかる。多次元の場合には偏微分に変えればよくて、 \[\nu_i=\frac{\partial E}{\partial J_i} \tag{4}\] だ。
次は量子の世界における振動数を考えてみよう。量子の世界の振動数は、ボーアのモデルによって軌道間の遷移によって説明されていた。 \[\nu_{mn} = \frac{E_m-E_n}{h}\tag{5}\] このしきにおいて、\(E_m\)というのは、量子条件 \[J=\oint pdq = mh\] によって決められるエネルギーなんだから、この作用変数の関数という意味で、\(E_m=E(mh)\)のような形式で書くことにしよう。すると、 \[\nu_{mn} = \frac{E(mh)-E(nh)}{h}\] となり、さらに\(E(mh)\)は\(m,n\)が非常に大きくてその差が非常に小さい場合、 \begin{align} E(mh) &= E(nh)+(m-n)h\frac{dE(mh)}{d(mh)}\\ &= E(nh)+(m-n)h\frac{dE}{dJ} \end{align} とかけるだろうから、 \[\nu_{mn} = (m-n)\frac{dE}{dJ}\tag{6}\] となっていることがわかる。これを(3)と見比べると、一般の場合においても量子数が十分大きいときには、確かに古典論と同じように取り扱って良さそうだ。
もうひとつ重要なこととして、(5)と(6)を比べることにより、 \[(m-n)\frac{dE}{dJ} \to \frac{m-n}{h}\frac{dE}{dn} \Longleftrightarrow\frac{E_m-E_n}{h}\tag{7}\] という対応が成り立っていることがある。これは暗に、量子数\(n\)によって決まる任意の物理量\(f(n)\)について、 \[\frac{m-n}{h}\frac{\partial f(n)}{\partial n} \Longleftrightarrow\frac{f_m-f_n}{h}\] が成り立つ(かもしれない)ことを示唆している。量子論における軌道番号の差\(m-n\)を\(k\)とするともうすこし使いやすい形になる。 \[\frac{k}{h}\frac{\partial f(n)}{\partial n} \Longleftrightarrow\frac{f_{n+k}-f_n}{h}\tag{8}\] また、振動数に対するこういう微分 \[k\frac{\partial \nu_{n+k,n}}{\partial n}\tag{9}\] というのを考えてみると、\(\nu_{n+k,n}\)というのは \[\nu_{n+k,n}=\frac{k}{h}\frac{\partial E(n)}{\partial n}\] であると考えられるから、つまり、 \[k\frac{\partial \nu_{n+k,n}}{\partial n}=k\frac{\partial }{\partial n}\left(\frac{k}{h}\frac{\partial E(n)}{\partial n}\right)\] となる。これは二階微分だから、差分で書くとするなら、 \[k\frac{\partial \nu_{n+k,n}}{\partial n}\Longleftrightarrow\frac{E(n+k)-E(n)-(E(n)-E(n-k))}{h} = \nu_{n+k,n}-\nu_{n,n-k}\tag{10}\] となるだろう。これは、遷移に対応して決まる量\(g_{n+k,n}\)に対して、 \[k\frac{\partial g_{n+k,n}}{\partial n}\Longleftrightarrow g_{n+k,n}-g_{n,n-k}\tag{11}\] が対応関係として成り立っていることを示唆する。つまり、エネルギーなど量子数によって確定する量に対しては(8)が、振動数など遷移に対応して(つまり量子数の差に対応して)決まる量に対しては(11)が対応関係として使われるべきである。