原子の構造・水素原子スペクトルとボーアの原子模型
1.原子の構造
光電効果なんかでわかるように、どうも物質は電子をその内部に含んでいるようだった。でも、現実の物質は電荷を帯びていないから、電子と逆の+電荷をもつものが、物質の中に存在するべきだろうと考えられた。
その+電荷はどのような形をしているかについて、ふたつモデルが作られた。一つは、正電荷が雲のように分布して、電子がその中に埋め込まれているモデル、もう一つは今考えられているような原子核と電子がそのまわりを回っているようなモデルである。
結局、ラザフォードによるα線の散乱実験の解析により、原子はどうも原子核+電子で構成されているらしいということが認められた。そのうち、電磁気学の方で散乱実験の解析を書くと思う。
ただし、原子核のまわりを電子が回るというモデルは、重大な問題を抱えていた。それは、電荷が加速度運動するとき、電磁波を放出して、エネルギーを失ってしまうという問題だ。エネルギーを失ってしまえば、電子は原子核に落ち込んで止まってしまう。でも、現実の原子では、ラザフォードの実験から、そんなことは決して無いとわかっているのだ。
2.水素原子のスペクトル
そんな問題を解決する最初のステップは水素原子のスペクトルにあった。水素原子を真空管のなかに少しだけいれて放電させると光を発するが、その波長は、バルマー系列と呼ばれ、それぞれ- Hα線:656.28nm
- Hβ線:486.13nm
- Hγ線:434.05nm
- Hδ線:410.17nm
その後、違う系列(m=1,3,4,5)も観測され、どうも(3)によって水素原子のスペクトルが決まっているらしいことが判明した。
\(R=4/364.56(\text{nm})=1.10\times10^7(\text{m}^-1)\)はいまではリュードベリ定数と呼ばれている。
3.ボーアのモデル
(3)式で水素原子のスペクトルが表せることが判明したのだが、なぜ、そんな式になるのか、ということは説明できなかった。そこにさっそうと登場したのがボーアである。
ボーアは、プランクとアインシュタインが導いた光のエネルギーに関する式 \[E=nh\nu\tag{4}\] に注目して、光のエネルギーがとびとびに決まるなら、電子のエネルギーもとびとびに決まってもいいんじゃないか?と考えたのだろう。そして、以下のようなモデルを考えた。
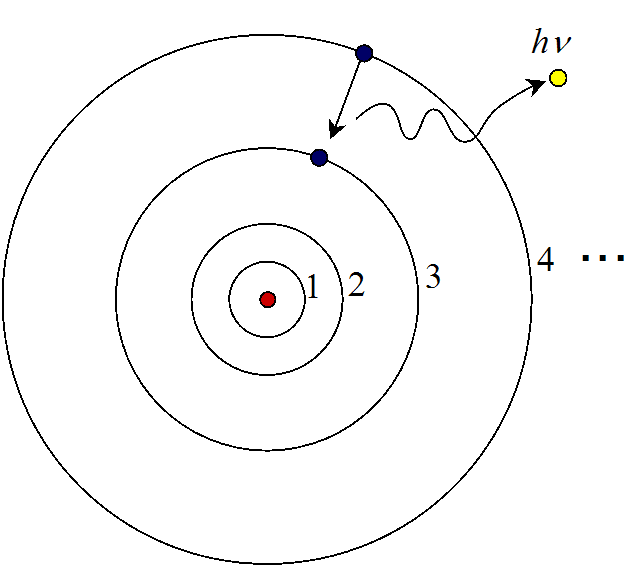
さらに、電子が外側の軌道から内側の軌道へとぴょこんと飛んだとき(
遷移
したとき)に、光子が一つ放出されると考えた。エネルギー保存則から、このとき出る光子のエネルギー\(h\nu\)は、電子のエネルギー差\(\Delta E\)に等しいはずである。また、原子が潰れていないのだから、遷移するとき以外は、電子は電磁波を放出しないとした。つまり、ひとつの軌道を回る状態では、電子はなぜだか分からないが、光を出さないと仮定するのだ。
ボーアはこういうモデルをたてたが、しかし、遷移というのがいつどうやってどのくらい起こるのかということには言及していないことに注意しておこう。遷移というのは考えてみれば不思議なことで、電子が瞬間移動するような現象である。普通の理論では説明できないだろう。
4.電子軌道のエネルギーと軌道半径
電子が軌道間を遷移するときにそのエネルギー差に相当する光を発するとしたのだから、スペクトルの規則を表すリュードベリの式 \[\frac{1}{\lambda}=R\left(\frac{1}{m^2}-\frac{1}{n^2}\right)\tag{5}\] を使えば、電子の軌道の様子がわかるんじゃないだろうか。そこで、まずは放出される光のエネルギーに直すため、両辺にhcを掛けて、 \[h\nu=hcR\left(\frac{1}{m^2}-\frac{1}{n^2}\right)\tag{6}\] としておこう。一方ボーアのモデルで、\(n\)番目の軌道から、\(m\)番目の軌道へ電子が落ち込むときのエネルギー差は、それぞれの軌道のエネルギーを\(E_n\)と表すことにすると、 \[\Delta E_{nm}=E_n-E_m\tag{7}\] となる。式の形を見ると、(5)と(7)は結構似ているじゃないか。どっちも引き算の形をしている。そこで(5)と(7)を対応させることで、電子の軌道のエネルギーを求めることができそうだ。エネルギー差\(\Delta E_{nm}\)が、放出される光のエネルギー\(h\nu\)に等しいとしたのだから、 \[E_n-E_m=hcR\left(\frac{1}{m^2}-\frac{1}{n^2}\right)\tag{8}\] となっているんだろう。つまり、おそらく、 \[E_n=-\frac{hcR}{n^2}\tag{9}\] が予想できる。
まずは類推でここまでたどり着いた。次に実際に電子のエネルギーを古典力学で計算してみよう。電子が感じる電気力は、軌道の半径を\(r\)とすると \[F(r)=\frac{e^2}{4\pi\epsilon_0 r^2}\tag{10}\] である。軌道を回る電子は、これと釣りあう遠心力をもって運動している。遠心力は、電子の速さを\(v\)とすると \[f(r)=\frac{mv^2}{r}\tag{11}\] である。ここから運動エネルギー\(mv^2/2\)を計算してみると、 \begin{align} \frac{mv^2}{r}&=\frac{e^2}{4\pi\epsilon_0 r^2}\\ \frac{1}{2}mv^2&=\frac{e^2}{8\pi\epsilon_0 r}\tag{13} \end{align} となる。電子のポテンシャルエネルギーは \[U(r)=-\frac{e^2}{4\pi\epsilon_0 r}\tag{12}\] なので、合計したエネルギーは以下のようになる。 \begin{align} E(r)&=\frac{e^2}{8\pi\epsilon_0 r}-\frac{e^2}{4\pi\epsilon_0 r}\\ &=-\frac{e^2}{8\pi\epsilon_0 r}\tag{13} \end{align} (9)と(13)を合わせれば、電子の半径を知ることができる。つまり、n番目の軌道を回る電子の軌道半径は、 \begin{align} E_n&=E(r_n) \\ -\frac{hcR}{n^2}&=-\frac{e^2}{8\pi\epsilon_0 r_n}\\ r_n&=\frac{e^2}{8\pi\epsilon_0 hcR}n^2 \tag{14} \end{align} である。
これで、ボーアのモデルが正しいとするなら、電子の軌道半径が(14)によって表されることが分かった。しかしながら、モデルの正しさはこれではわからない。このモデルが正しいことを示すためには、例えば、正体不明の定数\(R\)を導出できたりしないといけない。今のところ、\(R\)というのは実験的に定められた定数に過ぎないからだ。
5.リュドベリー定数の正体
ボーアのモデルが正しいと言えるのは、このモデルによって、リュドベリー定数の値を求めることができる点にある。早速それをやってみよう。まずおさえておくことは、円運動する電子が、古典論において、その角速度\(\omega\)と同じかその整数倍の振動数\(\nu_k=k\omega/2\pi\)の電磁波を放出するということだ。一方で、実際の水素原子の中で起きていることは、 \[E_n-E_m=hcR\left(\frac{1}{m^2}-\frac{1}{n^2}\right)\tag{8}\] というようなとびとびの変化である。しかし、すこし考えてみると、\(n\)と\(m\)が非常に大きくて、\(n=m+k, k<<n\)となっているとき、 \begin{align} E_{n}-E_{n-k}&=hcR\left(\frac{1}{(n-k)^2}-\frac{1}{n^2}\right)\\ &=hcR\left(\frac{2nk-k^2}{n^2(n-k)^2}\right)\\ &=\frac{2hcR}{n^3}k\frac{1-\frac{k^2}{n^2}}{(1+\frac{k}{n})^2}\\ &\approx\frac{2hcR}{n^3}k \end{align} と近似できる。つまり、このとき放出される光の振動数は \[\nu_k=\frac{2cR}{n^3}k\tag{15}\] によって与えられることがわかる。\(n\)が大きいときには、古典論の\(\nu_k=k\omega/2\pi\)と同じ形式で書けるのだ。
そこで、この式をつないでみよう。 \[\frac{2cR}{n^3}=\frac{\omega}{2\pi}\tag{16}\] 古典論における電子の角速度\(\omega\)はどうやって決まっていたのか考えると、これは遠心力とクーロン力の釣り合いによって決まる。 \[\omega^2=\frac{e^2}{4\pi\epsilon_0 mr^3}\tag{17}\] 古典論においては、この角速度と同じ周波数かその整数倍の周波数の電磁波が放出される。だから、(14)で求めた\(r\)を入れて、(16)に代入して計算すると、 \begin{align} \frac{4c^2R^2}{n^6}&=\frac{1}{4\pi^2}\frac{e^2}{4\pi\epsilon_0 m}\left(\frac{8\pi\epsilon_0 hcR}{e^2n^2}\right)^3\\ \frac{4c^2R^2}{n^6}&=\frac{1}{4\pi^2}\frac{e^2}{4\pi\epsilon_0 m}\frac{8^3\pi^3\epsilon_0^3 h^3c^3R^3}{e^6n^6}\\ c^2R^2&=\frac{8\epsilon_0^2 h^3c^3R^3}{me^4}\\ R&=\frac{me^4}{8\epsilon_0^2 h^3c} \end{align} となる。
このようにしてボーアモデルはこれまで実験的にしか分かっていなかったリュードベリ定数に物理的な説明を与え、物理学の世界で認められていくこととなった。