ボーア・ゾンマーフェルトの量子条件
1.ボーアの量子条件
下の図のような原子模型を提案し、原子のスペクトルに説明を与えたボーアだったが、それだけでは飽き足らず、ミクロの世界でなりったている基本法則とは何か、ということを探っていた。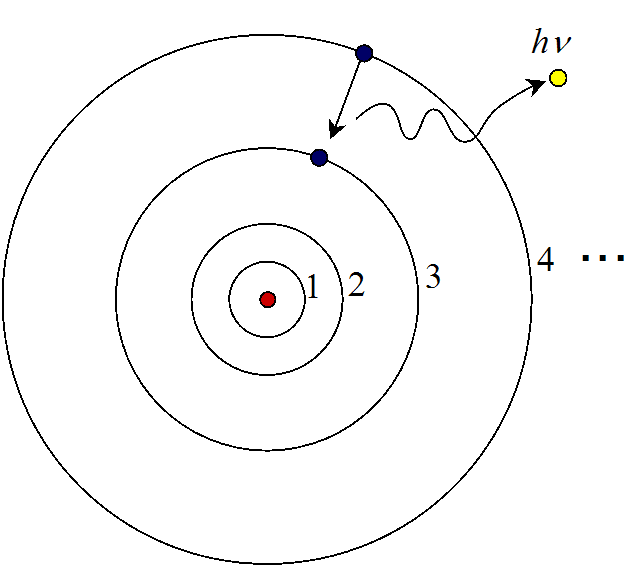
図のようなモデルを考えたとき、原子のスペクトルを与える法則から導き出されるn番目の電子の軌道半径が \[r_n=\frac{e^2}{8\pi\epsilon_0 hcR}n^2 =\frac{\epsilon_0 h^2}{\pi me^2}n^2\tag{1}\] となることは前回導出した。じゃあn番目の軌道を回る電子の角運動量\(J_n\)を考えてみよう。
まずn番目の軌道を回る電子の角速度は、クーロン力と遠心力の釣り合いから、 \begin{align} mr_n\omega_n^2&=\frac{e^2}{4\pi\epsilon_0r_n^2}\\ \omega_n&=\sqrt{\frac{e^2}{4\pi\epsilon_0mr_n^3}}\tag{2} \end{align} となる。したがって角運動量は \begin{align} J_n&=mr_n^2\omega_n\\ &=mr_n^2\sqrt{\frac{e^2}{4\pi\epsilon_0mr_n^3}} \\ &=\sqrt{\frac{me^2r_n}{4\pi\epsilon_0}}\\ &=\sqrt{\frac{me^2}{4\pi\epsilon_0}\frac{\epsilon_0 h^2}{\pi me^2}n^2}\\ J_n&=\frac{h}{2\pi}n \tag{3} \end{align} となっていることがわかる。
ディラック定数
\(\hbar=h/2\pi\)をつかって書くと、 \[J_n=n\hbar\tag{3'}\] である。これはいくらなんでもできすぎでは無いのか、と思えるくらいきれいな式が出てきてしまった。そこで、ここから考え方を180°変える。これまでは、現象論的に原子のスペクトルを表せるモデルとして、電子の軌道を考えてきたが、これからは、電子が(3)式を満たしているから、原子のスペクトルがそうなっていると考えるのだ。
電子の角運動量が\(\hbar\)の整数倍にならなくてはならない、という(3)式は今では
ボーアの量子条件
と呼ばれている。(3)式によって電子の取りうる角運動量が制限されているからこそ、スペクトルは離散的になるし、電子の軌道もとびとびになっているわけだ。2.ゾンマーフェルトの量子条件
ボーアが(3)のような量子条件を導いたあと、ゾンマーフェルトがさらに一般的な量子条件を導いた。というのも、ボーアの考案した(3)の角運動量に対する条件は、円運動にだけ適用可能なものであり、楕円運動や、もっと一般の運動には適用できなかったからだ。
こういう一般化をするときに役立つ力学といえば、解析力学である。ゾンマーフェルトはハミルトン・ヤコビの方程式から導かれる
作用変数
に注目した。作用変数とは(そのうち解析力学のほうで説明します。)、一般化運動量\(p_i\)と一般化座標\(q_i\)を用いて、 \[J_i=\oint p_idq_i\tag{4}\] と定義される量であり、(ハミルトニアンが時間に依存しないときは)時間に依存しない保存量である。さらに都合のいいことに、こいつの次元は角運動量と同じなのだ。ゾンマーフェルトは \[J_i=nh\tag{5}\] が量子化の条件であるとした。こうすることで、ボーアの角運動量に対する量子化条件を一般化し、水素原子スペクトルをさらに精度良く見積もることができるようになった。具体的には、(5)式をもとに楕円軌道を考えることで、今で言うp軌道やd軌道など、球対称でない軌道のエネルギーを考えることができるようになったのだ。
3.ハイゼンベルクの行列力学
原子から放出される光のスペクトルは(4)によってほぼ完璧に説明することができたのだが、その光の強さというのは全くわからなかった。放出される光の強さというのは、\(h\nu\)という光子のエネルギーが単位時間あたりどのくらい起こるかということを調べられればわかるだろう。
しかし、ボーアのモデルにおいて、光を放出するときに発生するとされる軌道間の遷移という現象は、いうなれば瞬間移動みたいなもので、その過程がどういうふうになぜ起こっているのかということを説明できそうもなかった。そんなことでは、どのくらい遷移が起こるかなんていうことは理論で求められそうもない。だいたい瞬間移動なんて常識に反している。
結局、量子力学はこの瞬間移動の原理についてはちょっとおいておいて、実験結果をとりあえず説明できる理論を構築することによって発展することになるのだ。次に活躍するのは天才ハイゼンベルクだ。ハイゼンベルクは前回ボーアモデルを導出したときと同じように、ニュートンの古典力学を量子力学に対応させ、行列力学を誕生させた。次回その様子を追っていくことにする。
余談になるけども、一般的な学校の量子力学の授業では、こういう実験から類推される理論をすっぽかして最初っからシュレディンガー方程式を始めてしまう。シュレディンガー方程式は比較的簡単な微分方程式だし、確かに学部1,2年にとってはこっちのほうが親しみやすいかもしれない。でも、シュレディンガー方程式ありきで議論を進められてしまうと、量子力学の原理がわからなくなってしまう気がする。
で、突然なんの脈絡もなしに(少し言いすぎかもしれないけど)、演算子がー、固有状態がー、固有値がー、という話が始まって、よくわからないことになってしまう。気がついたらなんか行列の方程式がでてきてるし。こういう(演算子とかの)発想が生まれるのは、シュレディンガーの前にハイゼンベルクが行列力学を始めていたからこそだと僕は思うんだ。
ともかく、ニュートンが天体の動きを説明するためにニュートン力学を創始したのと同じように、量子力学も原子のスペクトルから類推しながら、ミクロの世界を説明できる法則を四苦八苦しながら見つけていったものだということを忘れてはいけない気がする。