電子のスピン
1. Stern - Gerlachの実験
色々なところで解説されているだろうから、ここでは適当に紹介することにしよう。Stern-Gerlachの実験は、Ag原子のビームを(うまいこと作った)磁場中に通すと、2つのビームに分かれるという実験である。ちょうど下のような感じだ。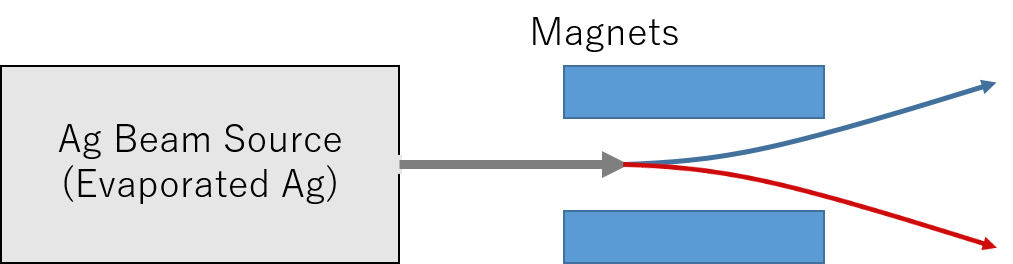
これを考えるために、原子のもつ磁気について最初に少し説明しておこう。
古典的な理論で行くと、原子核のまわりを電子が回っているのが原子という存在である。原子核のまわりを電荷が回っているのだから、これは円状の電流があるのと同じことで、こういう電流は磁気をもつ。その大きさは電流の大きさによって決まり、つまり電子の回る速さによって決まるのだ。古典的には、点電荷が円運動するときに作られる磁気双極子モーメント\(\b{\mu}\)は角運動量\(\b{L}\)に比例していて、 \[\b{\mu}=\gamma \b{L}\tag{1}\] の形で書ける。
量子力学では、角運動量は角運動量演算子によって置き換えられて、観測される角運動量は必ず角運動量演算子の固有値になる。原子の場合、全体の角運動量を表す\(\hat{l}^2\)の固有値は整数\(l\)によって\(\hbar l(l+1)\)のように離散化されていて、ある方向(z)のまわりを回転する角運動量\(\hat{l}_z\)の固有値は\(-l\leq m\leq l\)を満たす整数\(m\)によって\(\hbar m\)に離散化されていた。「交換関係から角運動量を解く」参照。
それに伴って、(1)式で表される磁気モーメントもある離散化された値しか取れなくなる。
ところで、Stern-Gerlachの実験は磁場を一方向にかける実験なので、磁場をかけた方向と同じ方向の磁気モーメント(すなわち角運動量)の大きさを見ていることに相当している。その方向への磁気モーメントがなければ磁場から力を受けずに直進するだろうし、あればその大きさに比例する力を受けて曲がるはずである。
よってビームが2つに分かれたという実験結果は、磁場方向への角運動量が2種類だけあったということを示す。しかも直進するものはなかったのだから、磁場方向への角運動量が0であるという状態はなかったということである。
これは原子の電子状態からは到底説明のつかないことだ。なぜなら、電子の軌道角運動量は\(-l\leq m\leq l\)を満たす整数\(m\)によって離散化されていて、\(l\)が整数なので、必ず奇数個の角運動量状態があるから。
偶数個に分かれるというのは、シュレディンガー方程式からはどうしても説明のつかないことだったのだ。
2.角運動量の交換関係に現れる可能性
そこで角運動量そのものについて見直してみる。角運動量演算子はもともと、古典論からの類推から、 \[\hat{\b{l}}=\hat{\b{r}}\times\hat{\b{p}}\tag{2}\] のように定義するのがいいだろう、というような感じで適当に考えられた。しかし、ハイゼンベルクやシュレディンガーの作り出した量子力学の骨格に戻って見ると、物理量の演算子というのは、交換関係を伴う形で考えられていた。必ず、とはいっても今のところ運動量演算子\(\hat{\b{p}}\)と位置演算子\(\hat{\b{r}}\)くらいのものかもしれないが。しかし、この2つの間に交換関係 \[[\hat{x},\hat{p}_x]=i\hbar\tag{3}\] が成り立つという条件をつけるだけで微分方程式を解くことなしに、調和振動子の問題なんかを解けたことを思い出そう。量子力学というのは交換関係が主要な役割を果たしているのかもしれない。(さらにいうなら、前回書いたように、位置演算子が\(\hat{x}=x\)、運動量演算子が\(\hat{p}_x=-i\partial_x\)と表されるのは、波動関数を位置の固有状態で展開したときだけなのだから、演算子の具体的な形は本質を表していないとも考えられる。)
そこで角運動量演算子の交換関係を原理としてみてみることにすると、実は奇跡的にも、角運動量が偶数個に離散化されるという可能性が、交換関係の中に隠れていたことが判明する。角運動量の交換関係を書いておくと、 \[[\hat{l}_x,\hat{l}_y]=i\hbar\hat{l}_z\tag{4}\] である。この交換関係は(2)のように角運動量を定義すれば、(3)の交換関係から導ける。簡単だからやってみるといいかもしれない。
そして、この角運動量の交換関係からから導き出されることは、\(\hat{l}^2,\hat{l}_z\)の固有値が \[\begin{align} \hat{l}^2\ket{lm} &= l(l+1)\hbar \\ \hat{l}_z\ket{lm} &= m\hbar &\left(m=-l,-(l-1),\ldots,0,\ldots,(l-1),l\right) \end{align}\tag{5}\] のように離散化されるということだった。
この固有値を導出したページの最後に少しだけ書いたように、(5)を満たす\(l\)は整数だけではない。実は1/2, 3/2, 5/2,...のような奇数の1/2も許される。代入してみれば、\(m\)の最大値と最小値がうまいこといってくれる。
そして、考えてみればわかるように、この\(l\)が1/2, 3/2, 5/2,...のときは\(\hat{l}_z\)の固有値\(m\)は偶数個になる!これはつまりある方向への角運動量が、偶数個の値しか取れないことを意味するのだ!
ということでStern-Gerlachの実験は角運動量の交換関係によって、自然に説明されてしまう。シュレディンガー方程式を解いただけでは説明できないのにも関わらず、だ。このことからも、量子力学で交換関係というものが非常に重要な役割を果たしていることがわかるだろう。
3.スピンという考え方
Stern-Gelachの実験でビームが偶数個に分離したことは、角運動量が交換関係を満たす何かである、と考えればうまいこと説明がつきそうなのだが、この1/2,3/2,5/2,...の角運動量は具体的にどういうものなのだろうか。\(l\)が整数の場合には、その状態を位置表示すれば、球面調和関数という波を描くことができて、イメージを掴むのはそこまで難しくなかった。しかし\(l=1/2\)の場合にはシュレディンガー方程式は波動関数の形を教えてくれないのだ。球面調和関数は、球対称なシュレディンガー方程式で、「空間的に一周すると波動関数がもとに戻る」という境界条件を考えることによって得られた解だ。そしてそのような解は、必ず\(l\)が整数でなければ存在することができない。すなわちStern-Gerlacの実験を説明するために考えなくてはならない\(l=1/2\)という状態は、「空間的に一周しても元の状態に戻らない」何かであると考えることができる。
しかし、空間的に一周しても元に戻らない関数なんて考えられるだろうか。普通に考えて、一周して元の場所に戻ってきたら、元と同じものが見えるはずだ。でも、Stern-Gerlachの実験(他にもいろんな実験はある。例えば磁場中でスペクトル線が偶数個に分かれるとか。)はそういう存在を示唆しているのだ。
結局、現在に至るまで、この\(l=1/2\)という状態を位置座標によって表現する方法は知られていない。それどころか、様々な実験からこの状態を空間の位置と紐付けて考えることは全くの見当違いで、物質のもつもう一つの性質であるとされている。
この性質は粒子自身の持つ角運動量なんだから、当初は多分自転のようなものなんじゃないかと考えられた。その頃の名残から現在でも