波動関数の正体 - 位置表示と運動量表示
1.物理量の確率
ある演算子\(\hat{F}\)で表される物理量が、ある値\(f\)を取る確率\(P(f)\)は、\(\hat{F}\)の固有関数\(\phi_f(x)\) \[\hat{F}\phi_f(x)=f\phi_f(x)\tag{1}\] を使って、シュレディンガー方程式\(\hat{H}\psi(x)=E\psi(x)\)の解\(\psi(x)\) (波動関数) を下のように \[\psi(x)=\sum_f A(f)\phi_f~もしくは~\psi(x)=\int A(f)\phi_fdf\tag{2}\] と展開した時の係数\(|A(f)|^2\)であるということにしたのだった。もう少し明示的に書くと、展開係数は \[A(f)=\int\phi_f^*(x)\psi(x)dx\tag{3}\] と計算できるから、確率\(P(f)\)は \[P(f)=\left|\int\phi_f^*(x)\psi(x)dx\right|^2\tag{4}\] であるということだ。今回はここから出発して、波動関数の正体に近づいていこう。
2.ブラケット表示
ここからはブラケット表示を使って行くことにするからさっきのをブラケットで書いておこう。ここでは\(\hat{F}\)に対して固有値\(f\)をもつベクトルを\(\ket{f}\)と書くことにする。つまり、 \[\hat{F}\ket{f}=f\ket{f}\tag{5}\] ということだ。これがさっきの\(\phi_f(x)\)に対応している。で、波動関数に対応するベクトルを\(\ket{\psi}\)と書くことにすると、(4)は \[P(f)=|\braket{f}{\psi}|^2\tag{6}\] となる。かなりシンプルに書けた。シンプルさというのは見通しを良くしてくれるから、とても大事である。3.電子をある位置に見出す確率・位置演算子の固有関数
さて、これまで波動関数を使うときには、\(|\psi(x)|^2\)が電子をある位置\(x\)に見出す確率密度であると考えてきた。これまではここから出発して理論を組み立ててきた。しかしだ。物理量の確率が(4)や(6)で与えられるということにしたのだから、当然物理量の一つである位置\(x\)も(4)や(6)によって確率を議論するべきではないだろうか。
つまり、位置演算子\(\hat{x}\)というのに対して、固有関数\(\phi_x(x')\) (\(\hat{x}\phi_x(x')=x\phi_x(x')\)) というのがあって、これをつかって、 \[P(x)=\left|\int\phi_x^*(x')\psi(x')dx'\right|^2\tag{7}\] もしくはブラケット表示では、\(\hat{x}\ket{x}=x\ket{x}\)というような固有ベクトル\(\ket{x}\)を使って、 \[P(x)=|\braket{x}{\psi}|^2\tag{8}\] のようにできるべきだ。
まずは(7)式から位置演算子の固有関数がどんなものになるべきか考えてみよう。このように考えていても、\(|\psi(x)|^2\)はやっぱり電子の位置に関する確率密度を与えているはずなので、 \[P(x)=|\psi(x)|^2\] であることから、 \[|\psi(x)|^2=\left|\int\phi_x^*(x')\psi(x')dx'\right|^2\tag{8}\] でないとおかしい。積分して元の関数に戻るようなことを実現できるのは、デルタ関数くらいしかありえない。よって\(\phi_x^*(x')=\delta(x-x')\)であり、実際、 \[\left|\int\delta(x-x')\psi(x')dx'\right|^2=|\psi(x)|^2\tag{9}\] が成り立っている。
4.(8)式の意味を考える
(7)から位置演算子の固有関数がわかったんだが、このページで言いたいことはそこじゃない。(8)が非常に重要だ。(8)をもう一回書いておくと、 \[P(x)=|\braket{x}{\psi}|^2\tag{8}\] であり、\(P(x)=|\psi(x)|^2\)を使うと、 \[|\psi(x)|^2=|\braket{x}{\psi}|^2\tag{9}\] となる。絶対値の二乗は外して、とりあえず位相は無視することにすれば、 \[\psi(x)=\braket{x}{\psi}\tag{10}\] を得る。これはどういう意味か考えよう。
もちろん、右辺を \[\braket{x}{\psi} = \int\phi^*_x(x')\psi(x')dx\] と解釈するのであれば、(10)はそれほどたいした意味はない。ただ単に積分を計算しなさいというだけだ。
しかし、ブラケット記法で書くと違うように解釈することもできる。少し抽象的な話になるが、ケット\(\ket{\psi}\)はベクトルで、\(\braket{x}{\psi}\)はベクトル\(\ket{x}\)との内積を取ることを意味していた。よって\(\ket{x}\)というベクトルの「長さ」が1に正規化されている(デルタ関数を正規化するというのはちょっと難しいから細かいことは置いておいて) と考えると、(10)は\(\ket{x}\)という軸上へ\(\ket{\psi}\)を射影するという意味をもつ。ちょうど下の図のような感じだ。
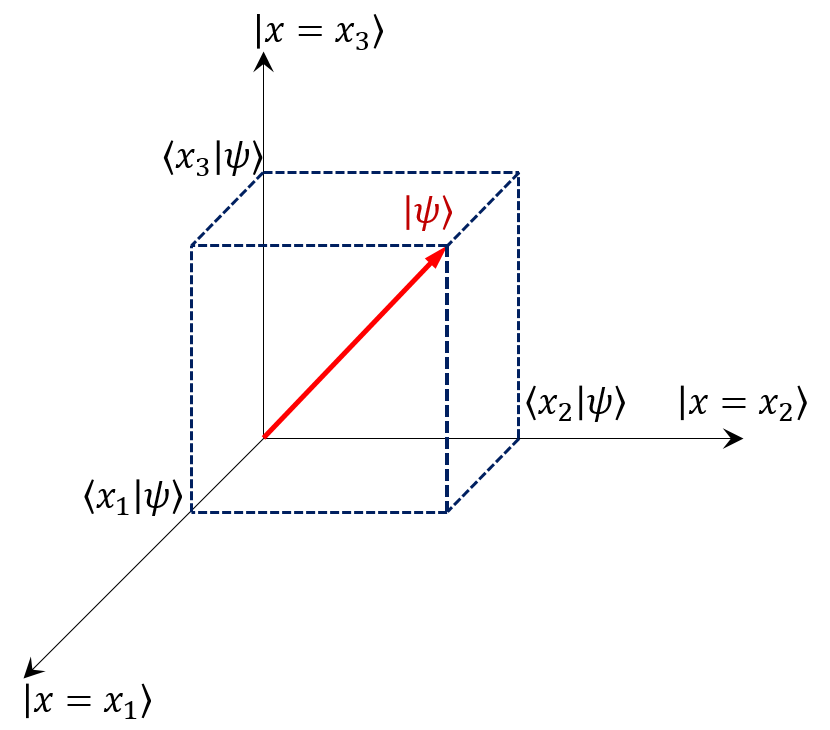
こんなふうに図的に表現すると、波動関数\(\psi(x)\)というのはある抽象的なベクトルの一つの表現に過ぎないことに気づける。\(\psi(x)\)というのは、ある状態を表すベクトルを、\(\hat{x}\)の固有状態\(\ket{x}\)を基底として表した姿に過ぎないのだ。そういう意味で、これまで波動関数と呼んでいたものは、位置表示と呼ばれる。
ということは、違う基底を持ってくれば、同じ状態のまた違った姿が見えるはずである。ちょっとやってみよう。
5.運動量表示
例えば運動量演算子\(\hat{p}\)に対する固有ベクトル\(\ket{p}\)によってある状態\(\ket{\psi}\)を展開するには、位置で展開したのと全く同じように、 \(\braket{p}{\psi}\)とすればいい。内積を取ったあとはただの数なので、\(\braket{p}{\psi}\)を\(p\)の複素関数\(\Psi(p)\)とみることができるだろう。つまり、 \[\Psi(p)=\braket{p}{\psi}\tag{11}\] とみるということだ。さて、運動量演算子\(\hat{p}\)は、波動関数を\(\psi(x)\)のように位置表示したとき、\(-i\hbar\frac{\partial}{\partial x}\)と表されるのだった。この演算子に対する固有関数は\(e^{-ipx/\hbar}\)である。代入してみればすぐにわかるだろう。しかし、ここまで話してきたことを踏まえると、固有関数という言い方も正しくないかもしれない。本当はこの固有関数というのは、\(\hat{p}\)の固有状態を位置表示したもの、と考えるのが自然だろう。つまり、 \[\braket{x}{p}=\sqrt{\frac{1}{2\pi\hbar}}e^{-ipx/\hbar}\tag{12}\] だということだ。ちなみに\(\sqrt{\frac{1}{2\pi\hbar}}\)というのは規格化に必要な因子である。
ここから(11)式、波動関数の運動量表示について考えよう。 (11)式はそのままだと計算の仕方がよくわからない。(11)というのは抽象的な内積を表しているだけだ。そこで、\(\ket{x}\)の完全性 \[\int dx\ket{x}\bra{x}=\hat{1}\] を使う。これを(11)に挿入すると、 \begin{align} \Psi(p)&=\bra{p}\hat{1}\ket{\psi} \\ &= \bra{p}\left(\int dx\ket{x}\bra{x}\right)\ket{\psi} \\ &=\int dx\braket{p}{x}\braket{x}{\psi} \\ \end{align} ということで、(10)、(12)を代入してやれば、(内積の順番が(12)と逆になっていることに注意する) \[\Psi(p)=\sqrt{\frac{1}{2\pi\hbar}}\int dx e^{ipx/\hbar}\psi(x)\tag{13}\] となり、これが波動関数を運動量表示したものである。\(\psi(x)\)や\(\Psi(p)\)というのはどちらも同じ状態ベクトル\(\ket{\psi}\)を違う座標系から見たというだけであって、どちらが本来の姿なのかということを考えるのは的はずれだ。
このようなことを考えてくると、僕には量子力学的な状態を抽象的なベクトル\(\ket{\psi}\)によって表すのが一番その本質を捉えているように感じられる。
しかしこのような見方が役に立つかと言われればそうでもない気がする。現実問題として、量子力学を使って何かを (例えば金属がなぜ電気を流すのか) を議論したいときに、そんなふうな抽象的なベクトルを考えていたところでなんの意味もない。結局重要になるのは、波動関数をシュレディンガー方程式 \[\hat{H}\psi(x)=E\psi(x)\] という微分方程式の解として求めて、許されるエネルギー準位だったり、状態を探すことである。その過程として(13)式のような式 (平面波展開) を使うことはあるだろうが、それはあくまで過程だ。
まあ応用面は置いておくことにすれば、僕はこの見方は結構面白いと思うな。スピンの考え方を理解するのにも、この概念があるのとないのとでは多分ぜんぜん違うと思う。
6.演算子の変換
ここまで波動関数の見方を変えるということをやってきたが、波動関数の見方を変えるときには、演算子の表現も変えてやらないといけない。例えば運動量表示された\(\Psi(p)\)に対して\(\hat{p}\)を作用させたときに、 \[-i\hbar\frac{\partial}{\partial x}\Psi(p)\] としていてはだめだろう。作用させた結果はいつでも0になってしまう。どうしたらいいか考えよう。ここでは一般論だけ書いておく。
まずは演算子\(\hat{A}\)を基底と関係する形で表してやらないといけないだろう。だから演算子が次のように適当な基底によって次のように書き換えられることを使う。 \begin{align} \hat{A}&=\hat{1}\hat{A}\hat{1} \\ &=\int dp \int dp'\ket{p}\bra{p}\hat{A}\ket{p'}\bra{p'}\\ &=\int dp \int dp'\bra{p}\hat{A}\ket{p'}\ket{p}\bra{p'}\\ &=\int dp \int dp'A_{pp'}\ket{p}\bra{p'} \end{align} これを使えば、任意の基底に対する演算子の表記がわかる。(ただし\(A_{pp'}=\bra{p}\hat{A}\ket{p'}\)が計算できることが必要だが。)
具体的にはどうやるのかというと、例えば波動関数の運動量表記 \[\Psi(p)=\braket{p}{\psi}\] を考えるときには、\(\hat{A}\)に対応する運動量表記での演算子を\(\hat{a}\)とすると、 \begin{align} (\hat{a}\Psi)(p) &= \bra{p}\left(\hat{A}\ket{\psi}\right)\\ &=\bra{p}\left(\int dp' \int dp''A_{p'p''}\ket{p'}\braket{p''}{\psi}\right)\\ &=\int dp' \int dp''A_{p'p''}\braket{p}{p'}\braket{p''}{\psi}\\ &=\int dp' \int dp''A_{p'p''}\delta(p-p')\Psi{p''}\\ &=\int dp''A_{pp''}\Psi{p''} \end{align} のような計算をすればいい。これで演算子の働きを積分表示したものが求まるということだ。