スピン一重項(Singlet)と三重項(Triplet) - 2電子系
1.反対称な波動関数
今回は、2つの電子が存在しているとき具体的にどのような状態が許されるのか、について書いてみたいと思う。電子2つを表す波動関数\(\psi(\b{r}_1,\b{r}_2)\)は、粒子を入れ替えるという操作に対して反対称で、つまり \[\psi(\b{r}_1,\b{r}_2) = -\psi(\b{r}_2,\b{r}_1)\tag{1}\] となっていないといけない。(1)式の理由として、電子はFermi粒子だから、というのもいいかもしれないが、僕はそれだと説明になっていないと思う。むしろ(1)を満たす粒子のことをFermi粒子だと言うのだから。(1)が成り立たないといけない、といえるのは、(1)を満たさないような実験が見つかっていないからである。
まあそんなことはともかく、具体的な問題を考えていこう。今回は簡単のために、一次元で無限の高さの量子井戸に閉じ込められた、2つの電子の波動関数が考えてみようと思う。一次元の量子井戸の問題は、大学で量子力学のまともな授業を受けた人なら必ず習う内容だと思うので、ここではシュレディンガー方程式から解いていくことはせずに、答えだけ最初にまとめておく。
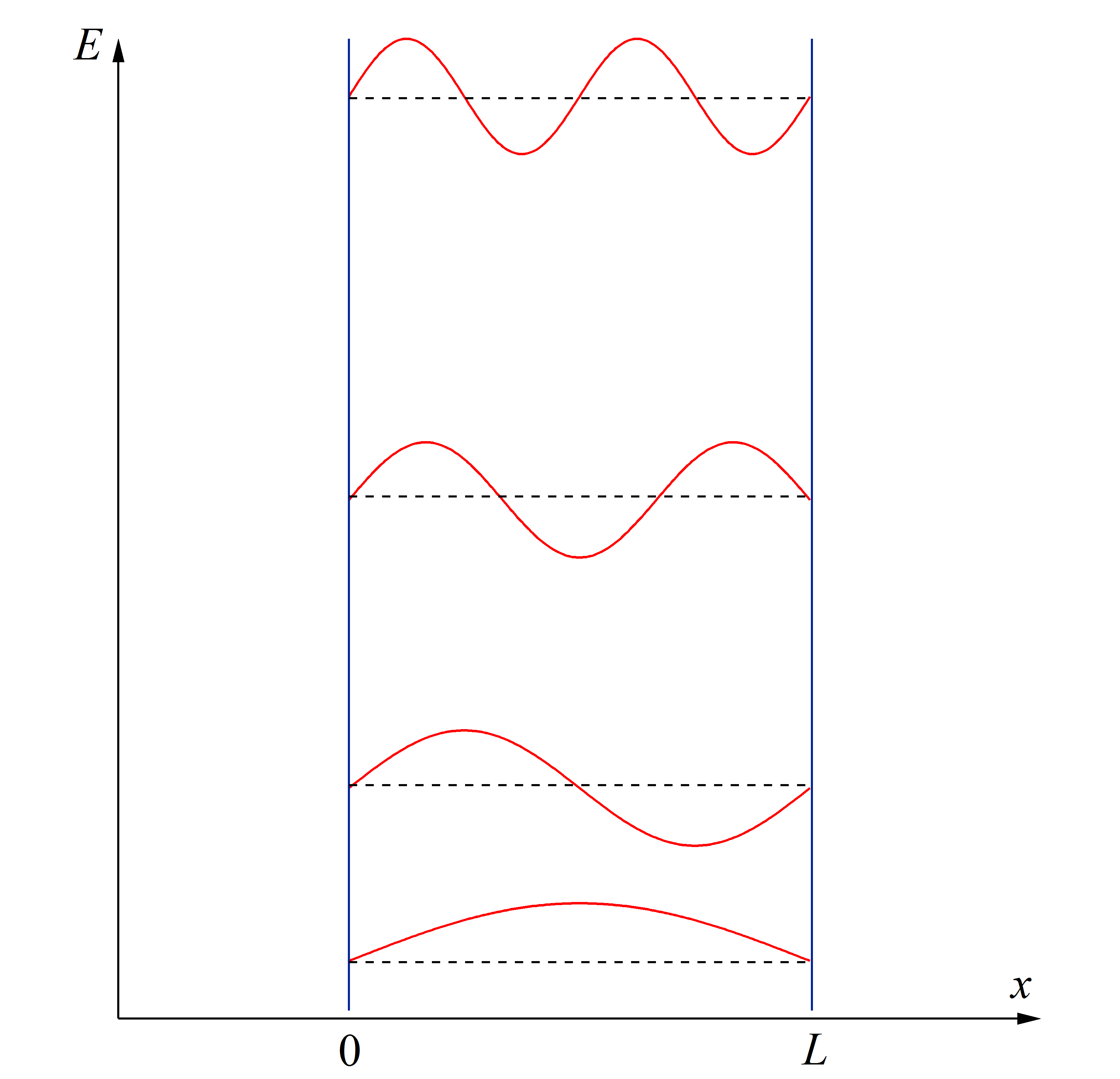
波動関数とエネルギー固有値は、 \[\phi_n(x)=A_n\sin\frac{n\pi x}{L}\tag{2}\] \[E_n = \frac{\hbar^2}{2m}\left(\frac{2\pi}{L}\right)^2n^2\tag{3}\] のような形で、図に書くと、
2.2つの電子の波動関数
簡単のため、2つの電子はクーロン力なんかで互いに力を及ぼしたりしていないことにする。そうするとシュレディンガー方程式は量子井戸の中で、 \[\left(\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x_1^2}+\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x_2^2}\right)\psi(x_1,x_2) = E\psi(x_1,x_2)\tag{4}\] の形となる。こういう形なら、\(\psi(x_1,x_2) = \phi^{(1)}(x_1)\phi^{(2)}(x_2)\)とおいて変数分離すれば、(4)式は次の2つの微分方程式に分離できる。(とりあえずどういう解が許されるのか考えたいので、\(\psi\)が反対称でないといけない、とかそういうことはとりあえずおいておく。許される解がどんなものなのかわかれば、あとでその解たちを組み合わせて、反対称な解とか対称な解とかを作ればいいのだ。) \begin{align} \frac{\hbar^2}{2m}\frac{d^2\phi^{(1)}}{dx_1^2} &= E^{(1)}\phi^{(1)}(x_1)\\ \frac{\hbar^2}{2m}\frac{d^2\phi^{(2)}}{dx_2^2} &= E^{(2)}\phi^{(2)}(x_2) \end{align} この式からわかることは、相互作用しない2つの電子の波動関数は、それぞれ独立した量子井戸の波動関数をかけ合わせたものになる、ということである。まあ当たり前かもしれないが。したがって、量子井戸の中の電子の波動関数は \[\phi_n(x)=A_n\sin\frac{n\pi x}{L}\tag{5}\] という式だったのだから、2つの電子の波動関数は \[\psi_{nm}(x_1,x_2) = \phi_n(x_1)\phi_m(x_2)\tag{6}\] のような形になる。ただし、これでは最初にいった反対称性\(\psi(x_1,x_2) = -\psi(x_2,x_1)\)が満たされていないので、もう少し工夫しないといけない。
さらに、ここまでは特に
スピン
には触れていなかったが、実は反対称性を考えるときにはスピンも考慮に入れる必要があるのだ。3.スピン状態の対称化
電子には空間的な波動関数という性質以外にも、スピンという性質を持っている。粒子の交換に対して反対称とか対称とか言うときには、粒子を入れ替えたときに電子のスピン状態の符号がどうなるか、ということも重要である。電子の状態は、その空間的な部分を表す\(\ket{\psi}\)と、スピン部分を表す\(\ket{\chi}\)の積で書くことができる。(本当は普通の積とは違うので、こういう言い方をすると怒られてしまいそうだがまあいいだろう。) つまり、 \[\ket{\psi}\ket{\chi}\] というのが電子の状態を表す。
さて、電子のスピンには上向き\(\ket{\uparrow}\)と下向き\(\ket{\downarrow}\)の2つの状態があるのだった。今回は2つの電子があるので、例えば\(\ket{\uparrow}_1\)を1つめの電子が上向きに存在している状態、のように書くことにすれば、すぐに思いつくスピン状態としては \begin{align} \ket{\chi} = \ket{\uparrow}_1\ket{\uparrow}_2,~~\ket{\uparrow}_1\ket{\downarrow}_2,~~\ket{\downarrow}_1\ket{\uparrow}_2,~~\ket{\downarrow}_1\ket{\downarrow}_2 \end{align} の4つがあるだろう。この状態の中で、2つのスピンが同じ方向を向いている状態 \[\ket{\chi} =\ket{\uparrow}_1\ket{\uparrow}_2,~~\ket{\downarrow}_1\ket{\downarrow}_2\tag{7}\] の2つは、粒子の交換に対して対称だ。(添字の番号を交換してもスピン状態の符号が変化しない。) よって、この状態に対しては、空間的な状態の項で反対称な項をくっつけてやれば、全体として反対称な状態を作り出すことができるだろう。 しかし、残りの2つの状態、 \[\ket{\chi} =\ket{\uparrow}_1\ket{\downarrow}_2,~~\ket{\downarrow}_1\ket{\uparrow}_2\] の2つは、粒子の交換をすると、全く違う状態になってしまう。これでは、電子の状態の反対称性 (粒子の交換をすると符号が反対になる性質) を満たすようにすることはできないだろう。そこで、この2つの状態を適当に組み合わせることによって、対称的な状態を作り出す。天下り的かもしれないが、 \[\begin{align} \ket{\chi} =&\frac{1}{\sqrt{2}}\left(\ket{\uparrow}_1\ket{\downarrow}_2+\ket{\downarrow}_1\ket{\uparrow}_2\right),\\ &\frac{1}{\sqrt{2}}\left(\ket{\uparrow}_1\ket{\downarrow}_2-\ket{\downarrow}_1\ket{\uparrow}_2\right) \end{align}\tag{8}\] という2つの状態を考えれば、+の状態は粒子の交換に対して対称的で、-の状態は粒子の交換に対して反対称な状態になっているだろう。これなら、電子が持つべき対称性を作り出すことができそうだ。
まとめると、2つの電子がある系では、 \[\ket{\chi}=\left\{\begin{align}&\ket{\uparrow}_1\ket{\uparrow}_2,~~\ket{\downarrow}_1\ket{\downarrow}_2,\\ &\frac{1}{\sqrt{2}}\left(\ket{\uparrow}_1\ket{\downarrow}_2+\ket{\downarrow}_1\ket{\uparrow}_2\right),\\ &\frac{1}{\sqrt{2}}\left(\ket{\uparrow}_1\ket{\downarrow}_2-\ket{\downarrow}_1\ket{\uparrow}_2\right) \end{align}\right.\tag{9}\] という4つのスピン状態を使えば、Fermi粒子としての反対称性を持たせることができるのである。
4.スピンシングレットとトリプレット
(9)の4つの状態が持っている角運動量で分類したものが、スピン一重項(Singlet)
・スピン三重項(Triplet)
と呼ばれる状態になる。それをここで説明しておこう。2つの角運動量があるときに、全体としての角運動量がどうなっているか、ということは角運動量の合成のページで詳しく書いた。詳しい計算とかはそっちで見てもらうことにして、今回はざっくりと説明する。
今回の場合、全角運動量を表す演算子は、 \[\hat{\b{s}}=\hat{\b{s}}_1 + \hat{\b{s}}_2\] とすればいいだろう。ただし、\(\hat{\b{s}}_1,\hat{\b{s}}_2\)はそれぞれ粒子1、粒子2に作用するスピン角運動量演算子を表す。全スピンの大きさを表す演算子\(\hat{\b{s}}^2\)と、z方向成分を表す演算子\(\hat{s}_z\)をさっきの4つの状態にかけてみると、実は(9)のやつは全てこの2つの演算子の固有状態になっている。
具体的にその固有値を表す量子数を書き出してみる。角運動量の大きさは\(\hat{\b{s}}^2\to s(s+1)\hbar\)、z成分は\(\hat{s}_z \to s_z\hbar\)という形式で書けるのだった。 \[\begin{align} \ket{\uparrow}_1\ket{\uparrow}_2 &\to &s_z = 1,s= 1\\ \frac{1}{\sqrt{2}}\left(\ket{\uparrow}_1\ket{\downarrow}_2+\ket{\downarrow}_1\ket{\uparrow}_2\right) &\to &s_z = 0,s= 1\\ \ket{\downarrow}_1\ket{\downarrow}_2&\to &s_z = -1,s= 1\\\\ \frac{1}{\sqrt{2}}\left(\ket{\uparrow}_1\ket{\downarrow}_2-\ket{\downarrow}_1\ket{\uparrow}_2\right)&\to &s_z = 0,s= 0 \end{align}\tag{10}\] となっている。計算は難しくないから自分でやってみるといいかもしれない。計算するときには、 \[\hat{s}_z=\hat{s}_{1z}+\hat{s}_{2z}\] \[\hat{\b{s}}^2 = \hat{\b{s}}^2_1 + \hat{\b{s}}^2_2 + 2\hat{\b{s}}_1\cdot\hat{\b{s}}_2\] を使えばいい。
ともかく、電子のスピン状態を対称化した4つの状態は、上の(10)式ような全角運動量をもっているのだ。結果を見ればわかるように、上の3つは全角運動量が\(s=1\)の状態で、最後の1つだけが\(s=0\)の状態になっている。こんなふうに、明らかに性質の異なる二種類の状態が出てくるので、この状態には特別な名前がついていて、\(s=1\)の3つが
スピントリプレット
、\(s=0\)の1つがスピンシングレット
と呼ばれる。ちょっとした補足。スピントリプレットの\(s_z=0\)の状態とスピンシングレットの状態は、それを表す式をひと目見ただけではあまり違いが見えないかもしれない。なんだかどちらも\(\ket{\uparrow}\ket{\downarrow}\)のような項からできていて、スピンが打ち消し合うような状態になっている気がしてしまう。しかし、トリプレットの\(s_z=0\)の状態は、スピンがz方向には回っていないが、xやy方向には回っている状態を表していて、シングレットはどの方向にも全く回っていない状態である。大雑把な言い方をすると、トリプレットの\(s_z=0\)の状態はz方向に関してだけスピンが打ち消しあっているような状態で、シングレットはどの方向に対しても打ち消しあっている状態と言ってもいいと思う
5.実際に電子の状態を構成してみる。
ちょっとスピンの話が長くなってしまったが、今回やりたかったのは、量子井戸に2つの独立な電子をいれたらどのように振る舞うか調べることだった。量子井戸の中の波動関数とエネルギー固有値は、 \[\phi_n(x)=A_n\sin\frac{n\pi x}{L}\] \[E_n = \frac{\hbar^2}{2m}\left(\frac{2\pi}{L}\right)^2n^2\] だった。最初に2つ電子がある場合のシュレディンガー方程式を考えて、2つの粒子があるときの波動関数は\(\phi_n(x_1)\phi_m(x_2)\)のように書けるということが分かったのだった。しかしこれからは波動関数で書くとちょっとめんどくさいから、\(\phi_n(x)\)に相当する状態を\(\ket{n}\)と表すことにしよう。つまり、 \[\phi_n(x) = \braket{x}{n}\] ということである。さて、この状態\(\ket{n}\)たちと、さっき考えたスピン状態を組み合わせて、電子の満たすべき対称性 (粒子の交換に対して反対称) をもった状態が具体的にどんな状態か考えよう。その前にちょっと準備で、スピン状態をいちいち(10)式のように書くのはめんどくさいから、トリプレットの状態を\(s_z=0,\pm 1\)に対応させてそれぞれ\(\ket{T_0},\ket{T_1},\ket{T_{-1}}\)と書いて、シングレットは\(\ket{S}\)と書くことにする。
さて、トリプレットの状態は、スピン側が粒子の入れ替えに対して符号が変わらないから、これとくっつける空間部分の符号が変わる必要がある。そんな状態は、たとえば \[\ket{\psi_{nm}^{(T)}} = \frac{1}{\sqrt{2}}\left(\ket{n}_1\ket{m}_2 - \ket{m}_1\ket{n}_2\right)\tag{11}\] というのが考えられるだろう。(11)の式の形を見ればすぐに分かるように、\(n=m\)のときには波動関数が消えてしまう。このことは、トリプレット状態では2つの電子が同じ空間的な状態をとることができないことを意味している。つまり、スピンが打ち消し合わないような状態では、同じ状態をとることはできないのだ。また、(11)式に今考えている系のハミルトニアンを掛けると、 \[E_{nm} = E_n+ E_m\] というエネルギーを持っていることがわかる。
一方で、シングレットの場合には、スピン側が反対称性を持っているから、空間側は対称的でないといけない。そういう状態は、 \[\ket{\psi_{nm}^{(S)}} = \frac{1}{\sqrt{2}}\left(\ket{n}_1\ket{m}_2 + \ket{m}_1\ket{n}_2\right)\tag{12}\] となる。こっちの場合には、両方ともが同じ状態(\(n=m\))になっても、状態が消えることが無いので、空間部分が同じ状態に入ることができる。シングレットはスピンが完全に打ち消し合っている状態だったから、このことはスピンが逆向きならば同じ状態に入れることを意味している。エネルギーはといえば、さっきと同じで、 \[E_{nm}=E_n+E_m\] である。
ということで、結局、量子井戸に閉じ込められた2つの独立した電子は、 \[\ket{\psi_{nm}^{(S)}}\ket{S},~\ket{\psi_{nm}^{(T)}}\ket{T_{0,\pm 1}}\] という状態を持てることがわかった。シングレットとトリプレットでは空間部分の粒子の交換について、対称性が逆になる。
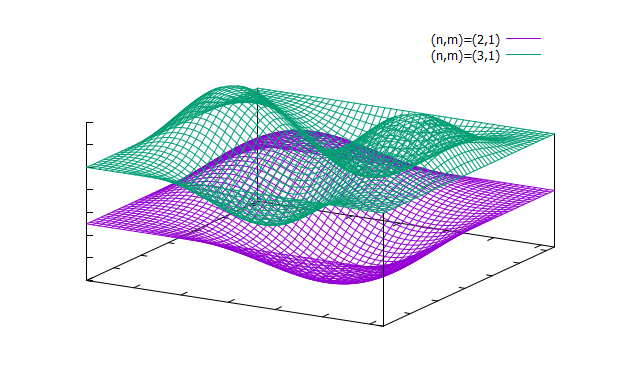
最後に、シングレットの空間部分と、トリプレットの空間部分の波動関数の様子をグラフにしてみた。
まずはシングレットのn=mの場合。