2粒子系・多粒子系
1.二電子系
まずは2つの電子がある系について、一般的な話をしていきたいと思う。2つの電子があるとき、シュレディンガー方程式や波動関数はどうなるだろうか。話を簡単にするため、最初は一次元で考える。
難しいことをする前に、まずは1つの電子の場合について復習しよう。1つの電子の波動関数\(\varphi(x)\)が満たすべき方程式は、 \[\left(\frac{\hbar}{2m}\frac{d^2}{dx^2}+V(x)\right)\varphi(x) = E\varphi(x)\tag{1}\] だ。これを解くことによって、電子がとることのできるエネルギー準位や、運動量・位置の期待値というのが求まる。そしてその結果は、例えば原子気体のスペクトル線を綺麗に説明することのできるものだったのだ。
さて、2つの電子を考えるときにはどうしたらいいか。これまで出てきたシュレディンガー方程式は、実は全て1つの電子についてのものだけだった。思い出すのは、行列力学と対比させながら導き出した「本来の形の」シュレディンガー方程式 \[\hat{H}\left(\hat{p},\hat{x}\right)\varphi(x) = E\varphi(x)\tag{2}\] である。この式の意味することろは、古典的ハミルトニアン\(H(p,x)\)の変数\(p,x\)を、形式的に演算子\(\hat{p},\hat{x}\)で置き換えたハミルトニアンに相当する演算子\(\hat{H}(\hat{p},\hat{x})\)の固有関数を見つけなさいよー、そうすればそのときの固有値が量子力学的に許されるエネルギーになっていますよー、ということだ。
ということは、2つの電子がある場合でも、その系の古典的なハミルトニアンを書いてやれば、どういう方程式を作ればいいかわかるはずだ。ハミルトニアンというのは大体エネルギーと同じことだから、1つめの電子が\(p_1\)の運動量で位置\(x_1\)にいて、2つめの電子が\(p_2\)の運動量で位置\(x_2\)にいるという状況を考えると、 \[H=\frac{p_1^2}{2m}+\frac{p_2^2}{2m}+V(x_1)+V(x_2)+U_{12}(x_1,x_2)\tag{3}\] である。ただし2つの電子は同じポテンシャルエネルギー\(V(x)\)を感じていて、しかも\(U_{12}(x_1,x_2)\)のような相互作用エネルギーをもっているとした。この相互作用エネルギーというのは、例えば静電気力 \[U_{12}(x_1,x_2) = \frac{e^2}{4\pi\epsilon_0 |x_1-x_2|}\] みたいなものを考えている。今回は別に具体的な波動関数を求めたいわけでは無いので、\(U_{12}(x_1,x_2)\)のように抽象的な形で書くことにしたのだ。
さて、(3)のようなハミルトニアンが出たので、これを(2)に書き直そう。それには運動量を\(-i\hbar d/dx\)と書き直せばいいから、 \[\left(\frac{\hbar^2}{2m}\frac{d^2}{dx_1^2}+\frac{\hbar^2}{2m}\frac{d^2}{dx_2^2}+V(x_1)+V(x_2)+U_{12}(x_1,x_2)\right)\varphi = E\varphi\tag{4}\] という方程式が、この場合に波動関数\(\varphi\)の満たすべき方程式である。
さて、すでに不思議なことが起こっているのだがわかるだろうか。
2.多電子系の波動関数はどこにいるのか
さて、さっきの方程式をしっかりみてみる。 \[\left(\frac{\hbar^2}{2m}\frac{d^2}{dx_1^2}+\frac{\hbar^2}{2m}\frac{d^2}{dx_2^2}+V(x_1)+V(x_2)+U_{12}(x_1,x_2)\right)\varphi = E\varphi\tag{4}\] この方程式から決まる波動関数\(\varphi\)は、まあ当たり前かもしれないが、\(x_1,x_2\)の関数になる。つまり\(\varphi(x_1,x_2)\)は二次元的な座標から決まる関数だということだ。でもよく考えてみれば、今考えていたのは一次元的に運動する電子のことだった。1つの電子ならその波動関数も一次元的に書けたけれども、2つの電子を考えようとすると二次元の波を使わないといけない。もはやこの電子の波は、一次元的な世界に存在するものではなくなってしまったのだ。
二次元の波ならまだイメージできてしまうが、じゃあ現実の世界に戻って、3次元的に運動する2つの電子を考えてみよう。すると、同じような考察によって、この2つの電子を表す波は6次元の世界に存在することになる。そんなものを図に書くことは不可能だし、想像することもままならない。結局、量子力学的なが2つ以上ある系では、波動関数を絵に書くことはできなくなってしまう。あとでこれについてもう少し詳しく書く。
でも、物理的な意味付けをすることは比較的簡単である。どうするのかというと、1つの電子が\(\b{r}_1\)、1つの電子が\(\b{r}_2\)に存在しているという確率密度が、 \[\left|\varphi(\b{r}_1,\b{r}_2)\right|^2 d\b{r}_1d\b{r}_2\] となっていると考える。そうだとするなら、2つの電子がどこかに見いだされる確率は1だから、以下のように波動関数を規格化しないといけない。 \[\int\left|\varphi(\b{r}_1,\b{r}_2)\right|^2 d\b{r}_1d\b{r}_2 = 1\tag{5}\] なぜこのような解釈をするのかと聞かれれば、それはこうすると「実験と合うから」だ。量子力学は、さっきの波動関数が6次元になるという話もそうだが、物理的直感があまりにも乏しい理論なので、出てきた結果が必ず実験と辻褄が合うように解釈しないといけない。 (ここが量子力学が難しく感じる理由な気もする。量子力学以外の物理は、それなりにみんなが納得できるような経験則に基づいて、それを少しずつ集めながら、整理しながら、作られてきたものだ。多分量子力学は、その現象を説明できる数式が発見されるのが早すぎたんだろう。)
3.電子は区別できない
\(\varphi(\b{r}_1,\b{r}_2)\)のような書き方をするのは、その根底から、2つ電子があったとき、その2つをこっちの電子・あっちの電子と「区別」することができるだろう、という考え方がにじみ出ている。しかし、本当にそうだろうか。この電子とあの電子にはどのような違いがあるのだろうか。電子、というからには、その質量もその電荷も全く同じ値だ。どのような観測をすれば、この電子とあの電子の違いを見つけることができるだろう。いや、そもそも同じ性質を持つもの、として考えているものの違いを見つけよう、というのが間違っている。この2つの粒子は、区別のしようが無いものである。
量子力学では位相の違いが物理量に何の影響も及ぼさなかったことを考えると、このような対称性は、\(\varphi(\b{r}_1,\b{r}_2)\)と粒子の座標を入れ替えた\(\varphi(\b{r}_2,\b{r}_1)\)という波動関数の間に \[\varphi(\b{r}_2,\b{r}_1) = C\varphi(\b{r}_1,\b{r}_2)\tag{6}\] という条件をつけることで実現できそうだ。この式は、粒子を入れ替えるという操作に対して、状態が全く同じ性質を保つことを表している。
(6)では位相\(C\)は、別に何の条件も無いのだが、粒子を2回入れ替えるという操作を考えることによって、\(C\)が満たさなければならない条件が導かれる。そこで、粒子を入れ替える操作をする演算子を\(P\)としよう。すると、(6)は \[P\varphi(\b{r}_1,\b{r}_2) = C\varphi(\b{r}_1,\b{r}_2)\] とも書けるだろう。もう一度作用させると、 \[P^2\varphi(\b{r}_1,\b{r}_2) = C^2\varphi(\b{r}_1,\b{r}_2)\] となるが、\(P\)を2回作用させるというのは、何もしないことと全く同じなので、 \[\varphi(\b{r}_1,\b{r}_2) = C^2\varphi(\b{r}_1,\b{r}_2)\] したがって、 \[C=\pm 1\tag{7}\] でなければならない。
つまり、粒子を入れ替えるという操作に対して、世界は次のようなことしか許さないのだ。 \[\varphi(\b{r}_1,\b{r}_2) = \varphi(\b{r}_2,\b{r}_1)\] \[\varphi(\b{r}_1,\b{r}_2) = -\varphi(\b{r}_2,\b{r}_1)\] このどちらが満たされているか、ということは粒子の種類によって実験で確かめていくほか無い。
しかし、これを確かめるとは言っても、どうやって確かめればいいのだろうか。
4.Bose粒子とFermi粒子
粒子の入れ替えに対する対称性は、同じ粒子がたくさん集まったときに現れる統計的な性質に大きく影響する。まず\(C=+1\)の方から。 \[\varphi(\b{r}_1,\b{r}_2) = \varphi(\b{r}_2,\b{r}_1)\] を満たすような粒子の種類は、
Bose粒子
と呼ばれる。このような粒子が集まると、ある温度での粒子のエネルギー分布はBose-Einstein分布
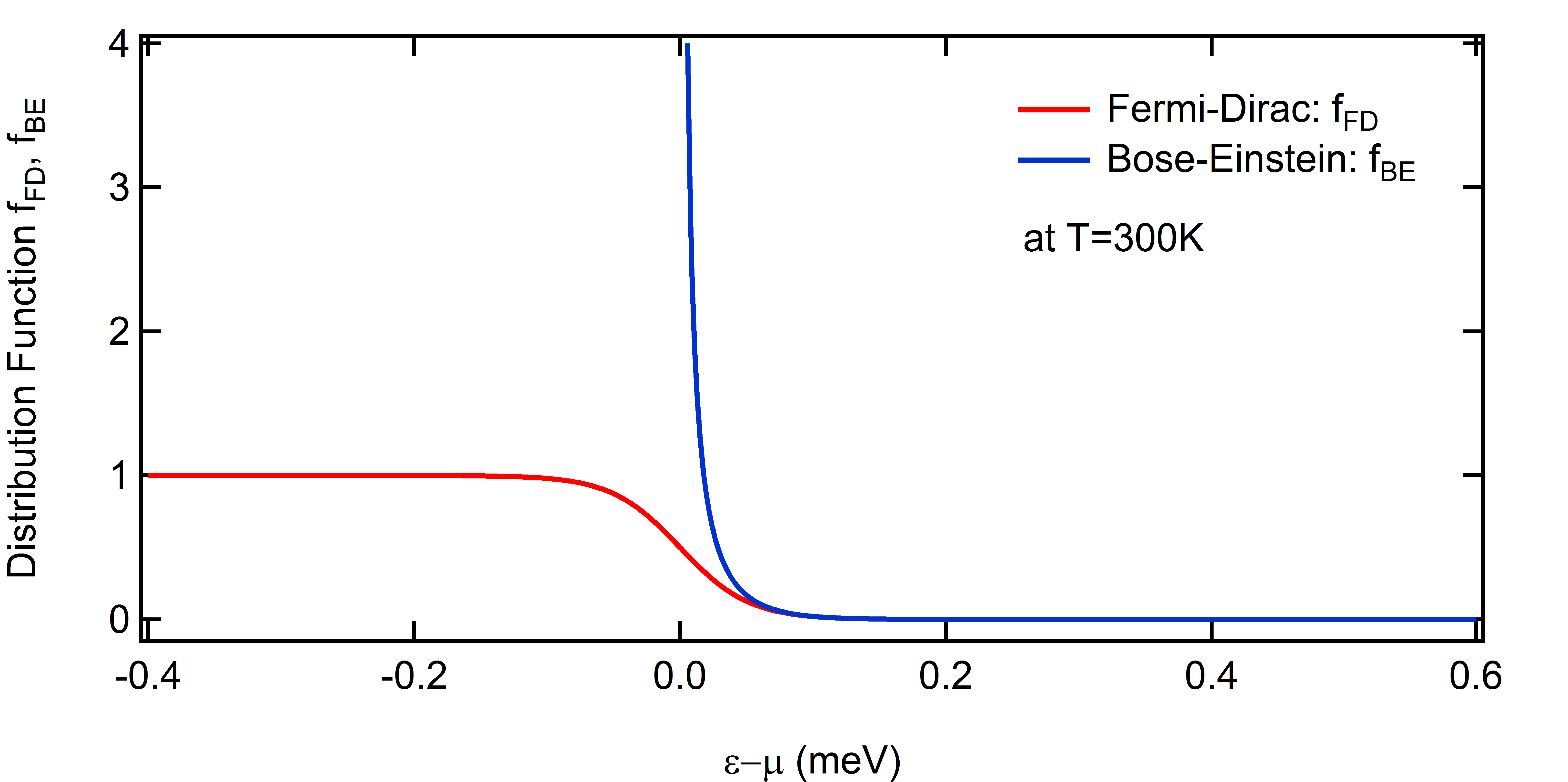
と呼ばれる分布になる。もし粒子が区別できてしまう場合には、このような分布を与えることは無い。具体的にどのような分布かというと、 \[f_{BE}(E)=\frac{1}{\exp\left(\frac{E-\mu}{kT}\right)-1}\] のようなやつである。(分布の導出はここ参照) このような分布がある種の粒子で実際に成り立っていることを実験的に確認するには、例えばBose-Einstein凝縮のような現象を観測すればいい。一方で\(C=-1\)の場合、つまり \[\varphi(\b{r}_1,\b{r}_2) = -\varphi(\b{r}_2,\b{r}_1)\] のときには、エネルギー分布は
Fermi-Dirac分布
となる。下のようなやつだ。 \[f_{FD}(E)=\frac{1}{\exp\left(\frac{E-\mu}{kT}\right)+1}\] 実は電子はFermi粒子なのだが、そのことは、例えば低温で金属の比熱がどのように振る舞うかということに密接に関係しているのだ。もし電子がFermi粒子的な性質を持っていなかったら、自然は今僕たちが見ているものとは全く違う様子になっていただろう。最後に二種類の分布関数のグラフを載せておく。