量子チャネル
1. デコヒーレンス
最初純粋状態 \(\ket{\psi}\) にあった量子状態が、時間の経過とともに「壊れて」しまい、混合状態になってしまう現象をデコヒーレンス
と呼ぶ。純粋な量子状態は通常とても壊れやすいものであり、そんな量子状態を応用しようとするときには、この壊れ方自身をしっかりとモデル化し、理解することが必要となる。量子チャネル
はそんなデコヒーレンスを記述する一つの考え方である。もともとは、量子状態を通信するときに生じるデコヒーレンスを記述するためのモデルとして考えられたためにこのような名前 (チャネル (channel) = 通信路) がつけられているが、量子チャネルの考え方はもっと一般的に適用できる。量子情報を勉強するには欠かせない概念である。2. モデル
デコヒーレンスの原因は、着目している系に準備した量子状態 \(\ket{\psi}\) が、周囲の環境系と勝手に相互作用してしまうことによる、とモデル化される。着目系 (S) と環境系 (E) の間に、自分たちの制御不可能な相互作用がある、というのがポイントである。最初着目している系 S にはある純粋状態 \(\ket{\psi}\) を用意したのだから、環境系 E とは全くエンタングルしていないと考えられて、このことを量子回路的に書くと、以下のようになる。エンタングルメントがあると、その部分系の状態は混合状態になってしまうのだった。(以前の記事参照)
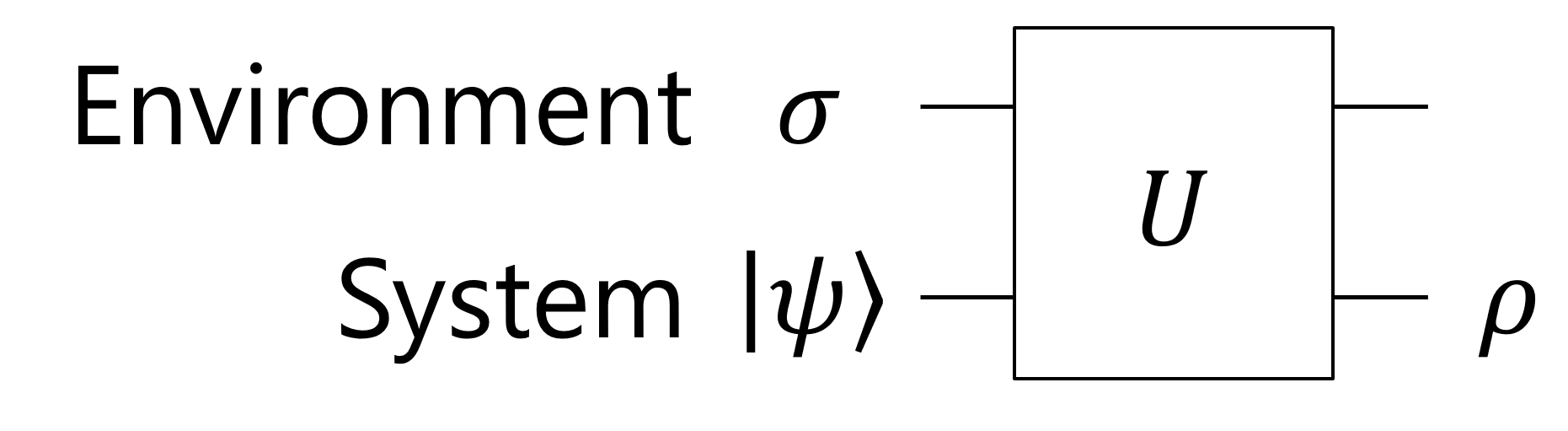
3. Kraus 演算子
形式的に書くだけであれば、上の形で事足りているのだが、実際に使うにはもう少しわかりやすい形に書き換えたほうが良いだろう。そこで登場するのが Kraus 演算子である。(1) 式をすこしずつ書き換えていこう。まず、環境系 E の初期状態 \(\sigma\) を、純粋状態 \(\ket{e_0}\) であるということにしてしまう。この操作は、混合状態には必ずそれを再現するような純粋状態が存在する (純粋化の記事参照) という事実によって正当化できる。
すると \begin{align} \rho = \Tr_E \left[U(\ket{e_0}\bra{e_0} \otimes \ket{\psi}\bra{\psi})U^\dagger\right] \tag{1} \end{align} と書ける。環境系の基底が \(\{\ket{e_i}\}\) であるとして、これを実際に計算すると、 \begin{align} \rho &= \Tr_E \left[U(\ket{e_0}\bra{e_0} \otimes \ket{\psi}\bra{\psi})U^\dagger\right] \\ &= \sum_i \bra{e_i} U(\ket{e_0}\bra{e_0} \otimes \ket{\psi}\bra{\psi})U^\dagger \ket{e_i} \\ \end{align} ここで演算子 \(K_i\) を、 \begin{align} K_i = \bra{e_i} U \ket{e_0} \end{align} と定義する。
これは \(U\) の環境系部分だけを内積によって消したような演算子なのだが、計算になれていないとこの演算子の正体がよくわからないと思うので、このページの最後に補足として具体的な計算方法を書くことにする。
この \(K_i\) を使えば、 \begin{align} \rho &= \sum_i K_i \ket{\psi}\bra{\psi} K_i^\dagger \end{align} を得る。先のトレースの入った形式よりはいくらかわかりやすい形となった。ここで定義した \(K_i\) がKraus 演算子
と呼ばれている。4. Kraus 演算子の性質
\(\rho\) のトレースが 1 になるという条件から、今考えているシチュエーションでは、 \begin{align} \Tr\rho &= \sum_i \Tr (K_i \ket{\psi}\bra{\psi} K_i^\dagger) \\ &= \sum_i \Tr ( K_i^\dagger K_i \ket{\psi}\bra{\psi}) \\ &= \Tr \left[\left(\sum_i K_i^\dagger K_i\right) \ket{\psi}\bra{\psi}\right] \\ &= 1 \end{align} を、任意の状態 \(\ket{\psi}\) について満たすはずである。そこで、 \begin{align} \sum_i K_i^\dagger K_i = I \end{align} が言える。ここで \(I\) は恒等演算子である。5. 量子チャネル
上で考えた量子チャネルの表現方法は、量子チャネルの演算子和表現 (operator-sum representation) とか、Kraus 表現とか呼ばれている。このように表現できる量子チャネル \(\Phi (\rho) = \sum_i K_i \rho K_i^\dagger\) は、以下の性質によって特徴づけられること (すなわち、ある演算子 \(\Phi\) が以下の性質を持つことと、Kraus 演算子による表現を持つことは同値であること) が知られている。
任意の密度演算子 \(\rho\) について
特に、下の2つの性質をまとめて、量子チャネルは- \(\Phi(\rho)\) は線形である。
- \(\Phi(\rho) = \Phi(\rho)^\dagger\)。つまりエルミート性を保存する。
- \(\Phi\) は完全正定値である。
- \(\Tr\left[\Phi(\rho)\right] = 1\)。つまりトレースを保存する。
CPTP 写像
(completely-positive trace-preserving map) である、ということもある。「完全正定値」という性質は聞き慣れないと思うので、ここで解説しておこう。\(n\times n\)次元の複素行列 \(\rho \in \mathbb{C}^{n\times n}\) を別の行列に変換する写像 \(\Phi\) が完全正定値であるとは、正定値の行列 \(\rho\) を変換したもの \(\Phi(\rho)\) が正定値となるというだけではなく、任意の自然数 \(k\) について、\(\mathbb{C}^{n\times n} \otimes \mathbb{C}^{k\times k}\) に属する \(nk\times nk\) の正定値行列 \(\rho'\) についても、\((\Phi\otimes \mathcal{I})(\rho')\) が正定値となることを言う。 要するに、大きな系の一部に対して量子チャネル操作をしても、その結果が密度行列としてふさわしいものになるという条件だ。
正定値ではあるが「完全」正定値ではないような写像の例として有名なものに、行列の転置操作がある。\(\rho \to \rho^T\) は \(\rho\) の正定値を保存するが、実はこの操作を大きな系の一部に行うと必ずしも正定値にならないことが知られている。例として 2 qubit の系の密度行列 \(\rho = \sum_{\{i,j,k,l\} \in \{0,1\}^{4}} \rho_{ijkl} \ket{i}\bra{j} \otimes \ket{k}\bra{l}\) の 1 番目の qubit の状態に関して転置をとる操作をした行列 \(T_1(\rho) = \sum_{\{i,j,k,l\} \in \{0,1\}^{4}} \rho_{jikl} \ket{i}\bra{j} \otimes \ket{k}\bra{l}\) は正定値にならないことがある。(そして、実はエンタングルメントのある状態でのみ、この操作で正定値でなくなるらしい。Peres–Horodecki criterion で検索。)
補足: \(\bra{e_i} U \ket{e_0}\) の計算
クラウス演算子 \(K_i = \bra{e_i} U \ket{e_0}\) の計算について。実際に計算する必要があるときは、以下のように計算すればよい。まず、\(U\) を環境系 E の基底 \(\{\ket{e_i}\}\) と着目系 S の基底 \(\{\ket{s_a}\}\) によって展開する。 \begin{align} U = \sum_{j,k} \sum_{a,b} u_{jk,ab}\ket{e_j}\bra{e_k}\otimes \ket{s_a}\bra{s_b} \end{align} そうしたらあとは簡単で \begin{align} \bra{e_i}U\ket{e_0} &= \sum_{j,k} \sum_{a,b} u_{jk,ab}\braket{e_i}{e_j}\braket{e_k}{e_0} \ket{s_a}\bra{s_b} \\ &= \sum_{j,k} \sum_{a,b} u_{jk,ab}\delta_{ij}\delta_{k0} \ket{s_a}\bra{s_b} \\ &= \sum_{a,b} u_{i0,ab} \ket{s_a}\bra{s_b} \end{align} もしある \(K_i\) をユニタリー操作から作ってその性質を調べたいというときには、この式から逆算して \(U\) を構成すればよい。