テレポーテーションと量子状態/量子チャンネルの双対性
テレポーテーション
量子テレポーテーションは、量子通信や量子計算、基礎的な量子情報理論にまで多大な影響を及ぼしているテクニックである。エンタングルした 2 qubit を使った量子テレポーテーションは以下のような量子回路によって表現できたのだった。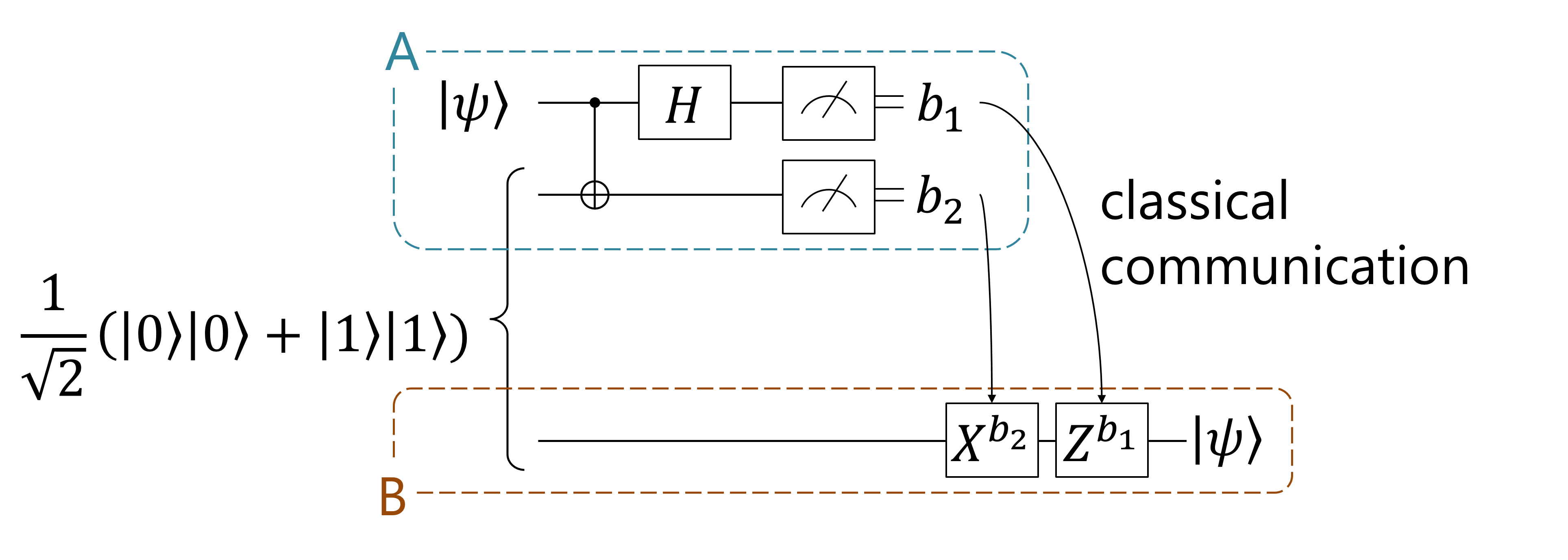
この記事は、そんな疑問に答えるための記事のつもりで書き、ついでに量子チャネルと量子状態の双対性に関しても少し触れる。
テレポーテーションのリソースとしての最大エンタングル状態
実は「最大エンタングル状態」の性質のうちたった一つが、この状態のテレポーテーションのリソースとしての資格を担保する。それは次の性質である。(この記事では式がごちゃごちゃすることを避けるために規格化定数を無視するが、規格化定数がついていないことに不安を感じる人は適宜補完してほしい。)
量子系 A, B の正規直交基底をそれぞれ \(\{\ket{a_i}_{i=1}^N\}, \{\ket{b_i}\}_{i=1}^N\) と置き、
\begin{align}
\ket{\Psi}_{AB} = \sum_i \ket{a_i}\ket{b_i}
\end{align}
とする。\(\ket{\Psi_{AB}}\) の A 系を \(\ket{\psi}_A = \sum_i \psi_i \ket{a_i}\) へと射影すると、B 系は \(\sum_i \psi^*_i \ket{b_i} := \ket{\psi^*}_B\) へと射影される。すなわち
\begin{align}
\bra{\psi}_A \ket{\Psi}_{AB} = \ket{\psi^*}_B \tag{1}
\end{align}
が成り立つ。
このことは以下の簡単な計算によって確かめられる。
\begin{align}
\bra{\psi}_A\ket{\Psi}_{AB} &= \left(\sum_j \psi^*_j \bra{a_j}_A\right)\left(\sum_i \ket{a_i}_A\ket{b_i}_B\right) \\
&= \sum_{i,j} \psi^*_j \braket{a_j}{a_i}\ket{b_i}_B \\
&= \sum_{i,j} \psi^*_j \delta_{ij}\ket{b_i}_B \\
&= \sum_i \psi^*_i \ket{b_i}_B \\
&= \ket{\psi^*}_B
\end{align}
この性質を下のような量子回路の形に書くと、テレポーテーションと密に関連していそうなことがよく分かると思う。(\(U_{\mathrm{ent}}\) は \(\ket{0}_A\ket{0}_B\) をエンタングル状態へと変換するゲートである。)
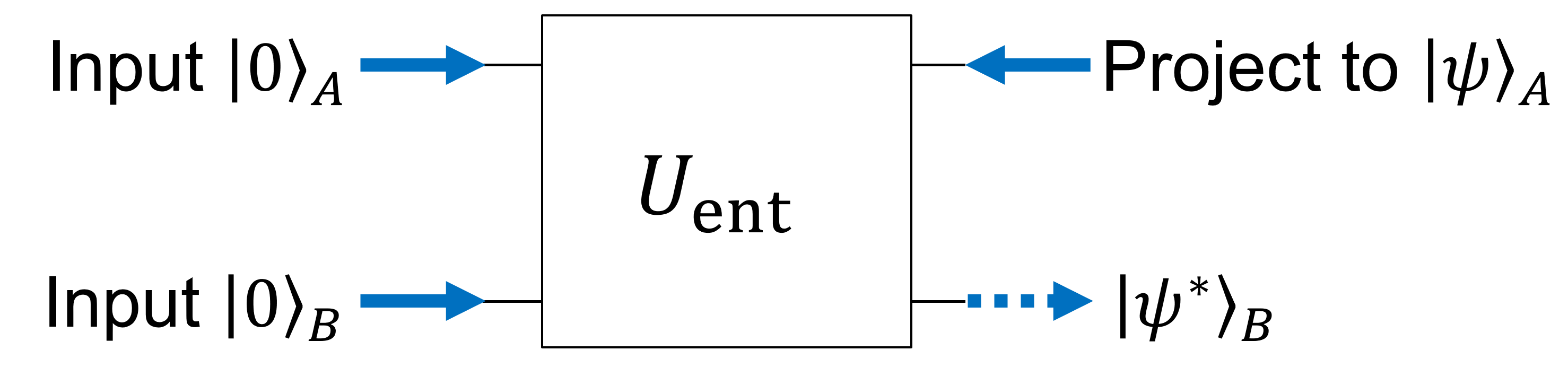
1 qubit のテレポーテーション
次に、(1) 式に基づいて、この記事の冒頭でも回路図を紹介した以下の標準的な量子テレポーテーションを考えてみよう。
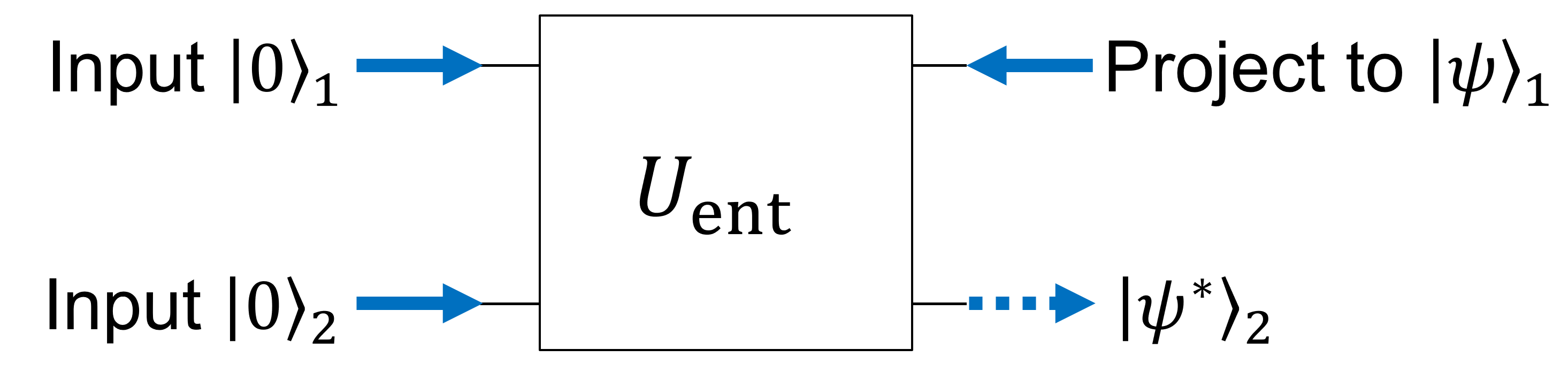
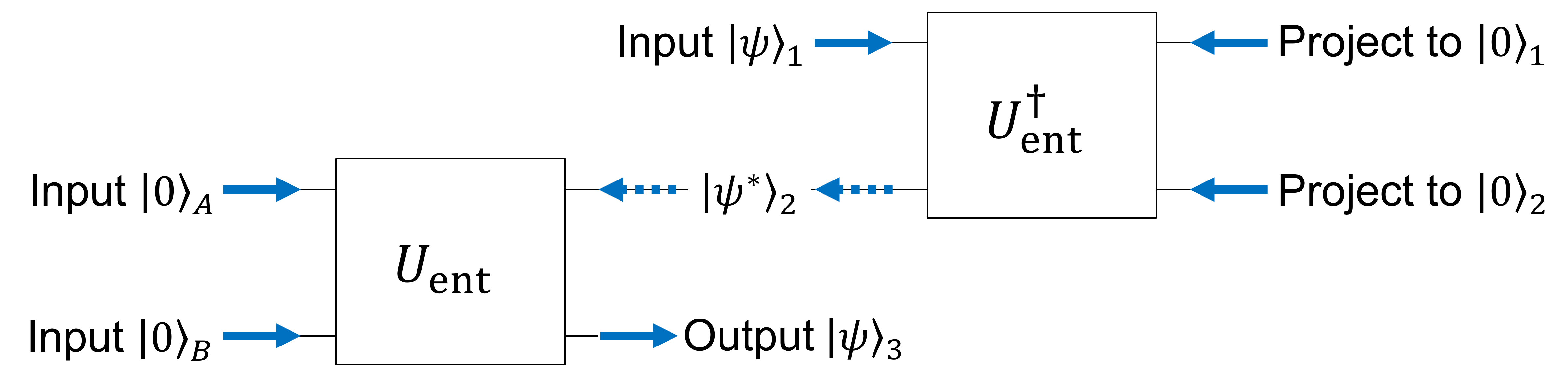
- A さん側で \(\ket{0}_1\ket{0}_2\) への射影が起こる。
- A さんと B さんが共有しているエンタングルペアのうち、A さんの片割れがあたかも \(\ket{\psi^*}\) へと射影されたかのような効果が現れる。
- 最大エンタングル状態の片割れが \(\ket{\psi^*}\) に射影されたことで、B さん側に \(\ket{\psi}\) が現れる。
A さん側が \(\ket{0}_1\ket{0}_2\) でない状態へ射影されてしまったときにはどうなるだろうか?これはそもそも、A さん側で CNOT→H のあと \(\ket{0}, \ket{1}\) 基底で測定することが、4つのベル状態 \begin{align} \ket{\Phi_0} &= \frac{\ket{00}+\ket{11}}{\sqrt{2}} \Leftrightarrow \ket{00}\\ \ket{\Phi_1} &= \frac{\ket{01}+\ket{10}}{\sqrt{2}}\Leftrightarrow \ket{01}\\ \ket{\Phi_2} &= \frac{\ket{00}-\ket{11}}{\sqrt{2}}\Leftrightarrow \ket{10}\\ \ket{\Phi_3} &= \frac{\ket{01}-\ket{10}}{\sqrt{2}}\Leftrightarrow \ket{11} \end{align} への射影と等価であることを考えて、(1) 式 \begin{align} \left(\sum_j \psi^*_j \bra{a_j}_A\right) \left(\sum_i \ket{a_i}\ket{b_i}\right) = \sum_i \psi^*_i \ket{b_i}_B \tag{1再掲} \end{align} とにらめっこすれば理解できる。A さんが \(\ket{00}\) を測定することは \(\ket{\Phi_0}\) への射影に相当しており、この状態は (1) 式において \(\ket{a_i} = \ket{b_i}\) であるような状態なので、B さん側にも全く同じ \(\ket{\psi}\) が届けられる。しかし A さんが \(\ket{01}\) を測定したとき、これは \(\ket{\Phi_1}\) への射影に相当するため、(1) 式において \(\ket{a_i} = X\ket{b_i}\) となってしまう。この基底変換はそのまま B さん側へと伝播して、B さんが受け取る状態は \(X\ket{\psi}\) となるのである。他の場合についても同様に考えると、A さんが \(\ket{10}\) を観測したとき \(\ket{a_i} = Z\ket{b_i}\) から B さんは \(Z\ket{\psi}\) を受け取り、\(\ket{11}\) を観測したとき \(\ket{a_i} = XZ\ket{b_i}\) だから \(XZ\ket{\psi}\) を受け取ることになる。これらをまとめると以下のような図が書ける。
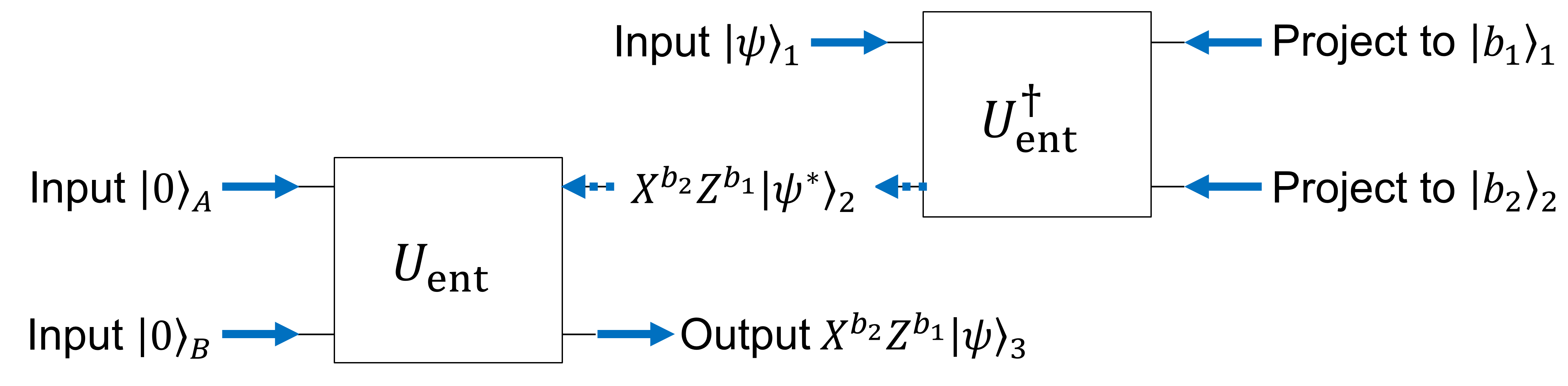
僕はこれでテレポーテーションが理解できた気になれたので、これが誰かの助けになればすごく嬉しい。
local な量子テレポーテーション
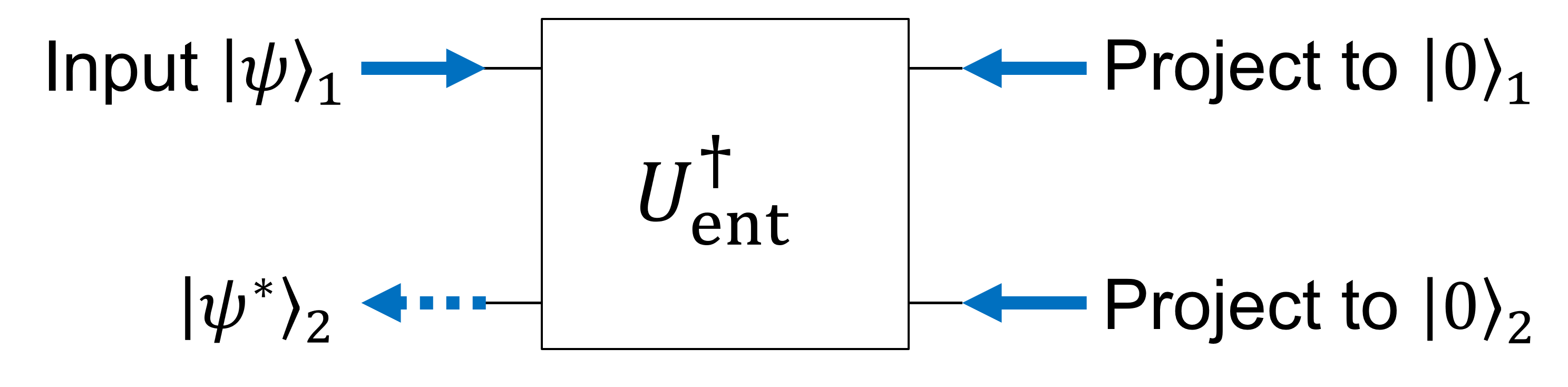
測定型量子計算なんかで使われるテクニックをついでに紹介したい。 (1) 式によるテレポーテーション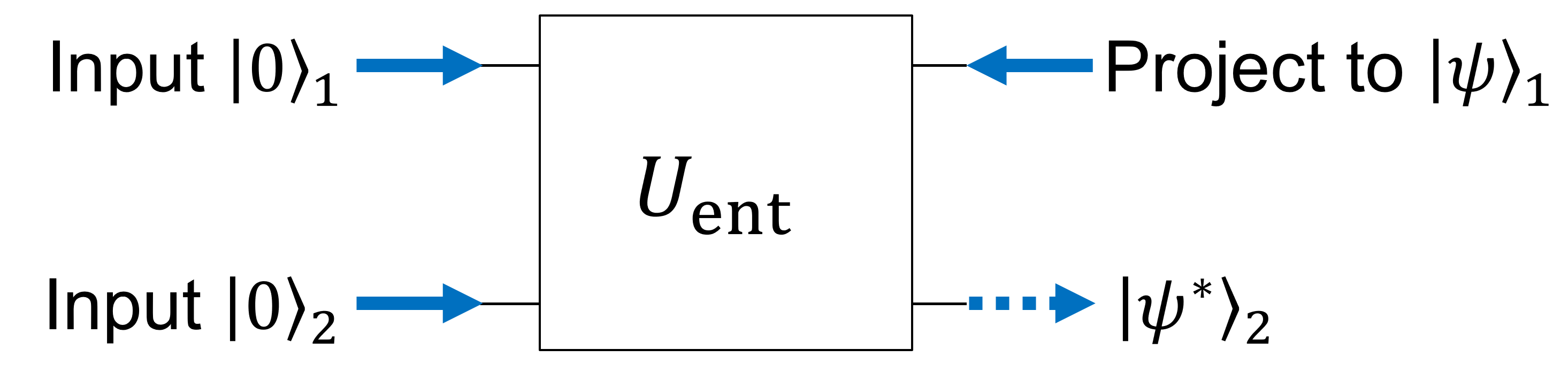

この直感を以下の簡単な 2 qubit の回路で検証してみる。上で書いた直感は、

納得行かない人は、\(\ket{1}\)に射影されてしまったときの状態を書き下して確かめてみよう。
このテクニックを大量に使って、エンタングルメントのリソースを消費しながら計算するのが、測定型量子計算である。(測定型量子計算では普通 CNOT ゲートではなくて CZ ゲートによって生成されたリソース状態を使うのが少しだけ異なる。)ちなみに、このテレポーテーションを local なテレポーテーションと呼ぶのが通例なのかどうかは定かでない。このページでそう呼ばれていたのでそうした。
量子チャネル - 量子状態の対応
(1) 式の性質から導かれるもう一つの大事な概念に、量子チャネルと量子状態の対応関係、界隈でChoi-Jamiołkowski isomorphism
と呼ばれるものがある。ここではこれを説明しよう。もう一度 (1) 式の図的表現を以下に示す。
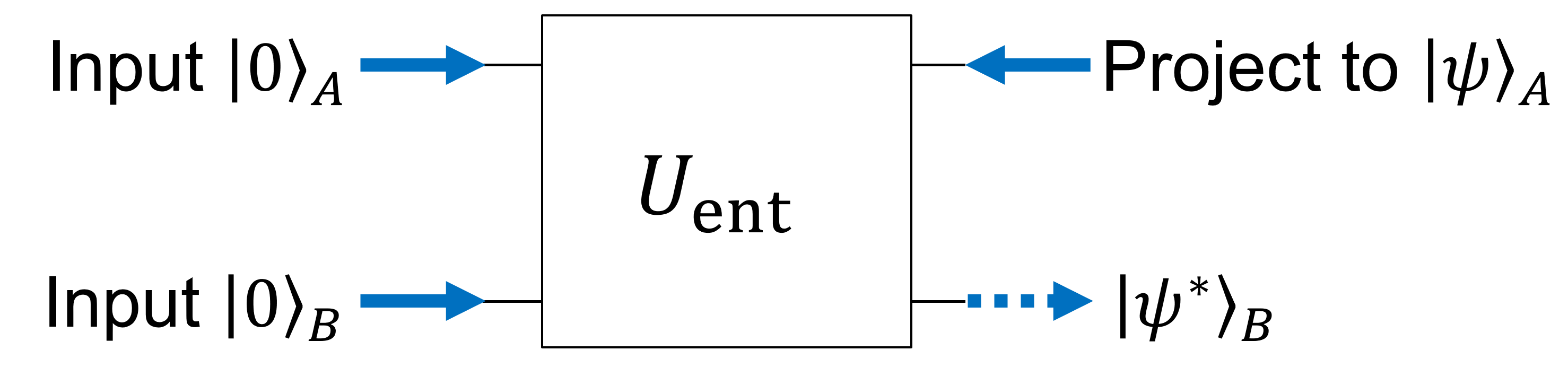
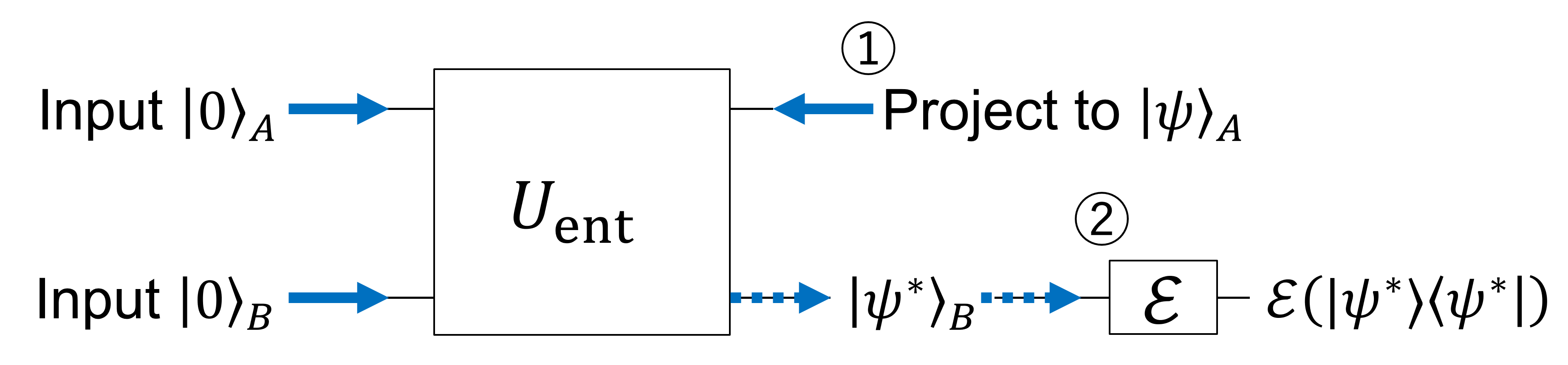
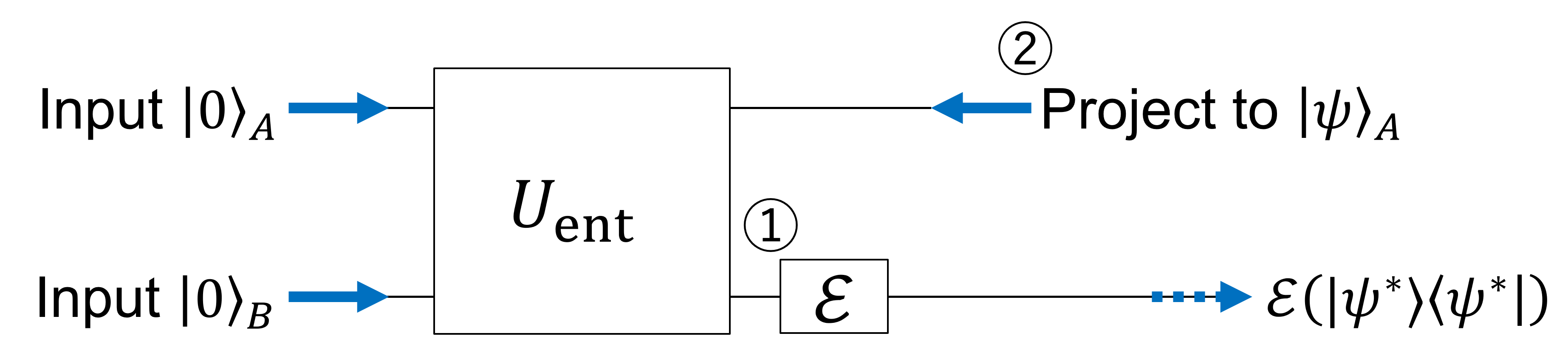
チャネル \(\mathcal{E}\) の Choi 状態
と呼ばれている。
Choi 状態:
\begin{align}
(\mathcal{I}\otimes \mathcal{E})\left(\ket{\Psi}\bra{\Psi}_{AB}\right) = \sum_{i,j} \ket{a_i}\bra{a_j} \otimes \mathcal{E}\left(\ket{b_i}\bra{b_j}\right)
\end{align}
Choi 状態と量子チャネルの対応付けが、Choi-Jamiołkowski isomorphismである。
これの何が "isomorphism" = 同型 なのかわからないが、なぜかそう呼ばれている。
この対応付けが有名なのは、あるチャネルの性質とそれに対応する Choi 状態の性質とがリンクしているからだ。例えば、- チャネル \(\mathcal{E}\) が completely positive ⇔ Choi 状態が positive. (Choi の定理)
- チャネル \(\mathcal{X}, \mathcal{Y}\) について \(\mathcal{Y}(\rho)=\mathcal{Z} (\mathcal{X}(\rho))\) を満たす \(\mathcal{Z}\) が存在する。⇔ \(\mathcal{X}, \mathcal{Y}\) に対応する Choi 状態 \(\rho_{\mathcal{X}}, \rho_{\mathcal{Y}}\) について、\(I(\rho_{\mathcal{X}}) \geq I(\rho_{\mathcal{Y}})\) (\(I\) は相互情報量).
おまけ: 1 qubit のテレポーテーション
(1) 式の図的な表現をみると、何も A さん側で 2 qubit 使わなくてもテレポーテーションが実現できそうである。そこでエンタングル状態 \(\ket{\Psi}_{AB} = (\ket{00} + \ket{11})/\sqrt{2}\) の 2 qubit のみを使ったテレポーテーションを考えてみよう。普通、実験的には \(\ket{0}, \ket{1}\) への射影測定しかできないので、(というか射影測定のできる状態を基底として使っているという方が正しいかもしれないが、) \(\ket{\psi}\) へ射影するという操作には、\(\ket{0}\) を \(\ket{\psi}\) へと変換するユニタリゲート \(U_\psi\), \begin{align} U_\psi \ket{0} = \ket{\psi} \end{align} が必要となる。ユニタリ性から、\(U_\psi\) は \(\ket{1}\) を \(\ket{\psi}\) と直交した状態へと変換する。したがって \(\ket{1}\) は \(U_\psi\) によって \begin{align} U_\psi \ket{1} &= \beta^*\ket{0} - \alpha^*\ket{1} \\ &:= \ket{\psi^\perp} \end{align} へと変換される。
さて、この \(U_\psi\) を使って \(\ket{\psi}\) への射影を行うには、まず逆変換 \(U^\dagger_\psi\) を \(\ket{\Psi}_{AB}\) のA側に作用させたあとに \(\ket{0}, \ket{1}\) 基底で測定すればよい。このとき測定結果 \(\ket{0},\ket{1}\) によってそれぞれ \begin{align} (\ket{0}\bra{0}_A \otimes I ) (U^\dagger_\psi\otimes I) \ket{\Psi}_{AB} &= (\ket{0}\bra{\psi}_A \otimes I )\ket{\Psi}_{AB}\\ &= \ket{0}_A\ket{\psi^*}_B\\ (\ket{1}\bra{1}_A \otimes I ) (U^\dagger_\psi\otimes I) \ket{\Psi}_{AB} &= (\ket{0}\bra{\psi^\perp}_A \otimes I )\ket{\Psi}_{AB}\\ &= \ket{0}_A\ket{\psi^{\perp *}}_B \end{align} という状態へと収縮する。上が \(\ket{0}\) が観測された場合、下が \(\ket{1}\) が観測された場合である、A で \(\ket{0}\) が観測された場合には、前のセクションで書いたように、\(\ket{\psi^*} = \alpha^*\ket{0} + \beta^*\ket{1}\) が「テレポート」される。\(\ket{\psi}\) を送りたければ、\(U_{\psi}\) の代わりに \(U_{\psi^*}\) を使えば良いので、これで量子テレポーテーションという目的が達成できているといえるだろう。
一方で、\(\ket{1}\) が観測されたときには、 \begin{align} \ket{\psi^{\perp *}} &= \beta\ket{0} - \alpha\ket{1} \end{align} という状態へと収縮している。これを見ると、 \begin{align} \ket{\psi^{\perp *}} &= XZ\ket{\psi} \end{align} となっていることに気づく。したがって、A側で \(\ket{1}\) が観測された、という情報を知ることができれば、\(\ket{\psi^{\perp *}}\) に対して \(X\) ゲート、\(Z\) ゲートの順番でゲートを作用させれば、\(\ket{\psi}\) を復元できる。このプロトコルを図に書くと以下のようになる。
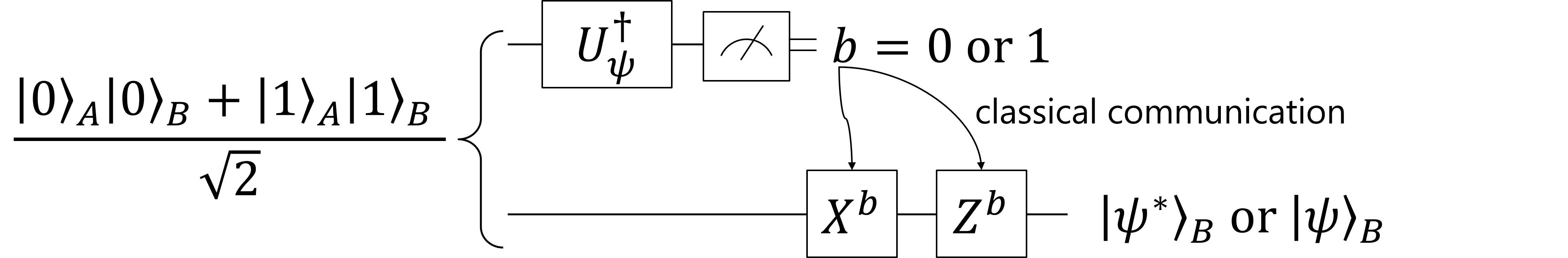
複素共役をとる、という操作をすればいいじゃないか、と思われるかもしれない。しかし実は複素共役をとるという量子操作は実現できない。密度行列で考えると、これは \(\rho \to \rho^* = \rho^T\) (T は転置) という操作であり、前回の記事 で少し触れたように非物理的な操作になってしまう。