量子テレポーテーション
1. 量子テレポーテーションとは
量子テレポーテーションとは、適当な量子状態 \(\ket{\psi}\) を遠隔地に送り届けるためのテクニックである。このテクニックに必要なものは- 送信者と受信者が、互いにエンタングルした量子系を保持していること。
- 送信者と受信者が通信路を確保していること。(古典情報がやり取りできれば良い。)
2. 1 qubit の量子テレポーテーションのアルゴリズム
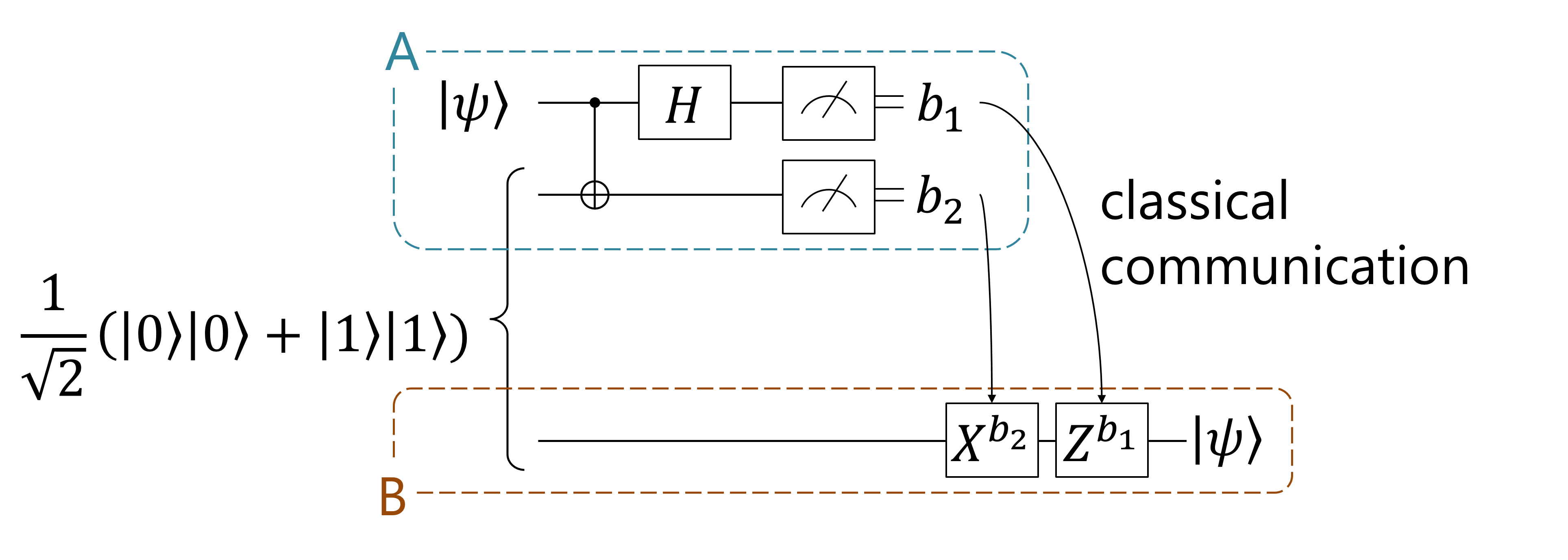
1 qubit の任意の量子状態 \begin{align} \ket{\psi} = \alpha\ket{0} + \beta\ket{1} \end{align} を A さんから B さんに送り届けるやり方を説明しよう。実は 1 qubit の量子状態を送るには、エンタングルした 2 つの qubit の片割れを A, B がそれぞれ持っていれば十分である。通信のリソースとなるエンタングルした 2 つの qubit を \begin{align} \frac{1}{\sqrt{2}} \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right) \end{align} と書くことにしよう。添字はそれぞれの qubit を A, B が持っていることを表している。(この 2 つの qubit は遠隔地にある。)さて、全体の初期状態は、はじめ \(\ket{\psi}\) という量子状態を A さんが持っているのでそのことも加味して、 \begin{align} \frac{1}{\sqrt{2}}\ket{\psi}_A \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right) \end{align} となる。この初期状態から次のようなアルゴリズム (量子テレポーテーション) を使うことで A さんは B さんに \(\ket{\psi}\) を送信できる。
A さんの作業:
量子回路で表すと以下のようになる。
- \(\ket{\psi}_A\) からエンタングルした量子ビットの片割れに controlled-NOT ゲートをかける。
- \(\ket{\psi}_A\) にアダマールゲートをかける。
- 2 つのビットを 0, 1 測定する。測定結果を \(b_1\), \(b_2\) とする。
- 測定結果 \(b_1\), \(b_2\) を B さんに伝える。
- A さんの測定結果を受け取る。
- \(b_2\) が 1 だったらエンタングルの片割れに X ゲートをかける。
- \(b_1\) が 1 だったらエンタングルの片割れに Z ゲートをかける。
- もともとのエンタングルした片割れは \(\ket{\psi}\) に等しくなっている。
3. 量子テレポーテーションの数式
1 ステップごとに量子状態を追っていき、上で示した量子テレポーテーションのアルゴリズムが正しいことを確かめよう。 初期状態は \begin{align} \frac{1}{\sqrt{2}}(\alpha\ket{0}_A+\beta\ket{1}_A) \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right) \end{align} である。最初の CNOT ゲートで、量子状態は \begin{align} &\frac{1}{\sqrt{2}}[\alpha\ket{0}_A\left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right) \\ &\qquad +\beta\ket{1}_A\left(\ket{1}_A\ket{0}_B + \ket{0}_A\ket{1}_B\right)] \end{align} に変化する。次のアダマールゲートでは、少しめんどくさい計算だが、 \begin{align} &\frac{1}{2}\ket{0}_A\ket{0}_A(\alpha\ket{0}_B + \beta\ket{1}_B) \\ &+\frac{1}{2}\ket{0}_A\ket{1}_A(\alpha\ket{1}_B + \beta\ket{0}_B) \\ &+\frac{1}{2}\ket{1}_A\ket{0}_A(\alpha\ket{0}_B - \beta\ket{1}_B) \\ &+\frac{1}{2}\ket{1}_A\ket{1}_A(\alpha\ket{1}_B - \beta\ket{0}_B) \end{align} となる。最初の 2 qubit の 0, 1 を測定すると、その結果に応じて状態が収縮する。 \begin{align} 00 &\to \ket{0}_A\ket{0}_A(\alpha\ket{0}_B + \beta\ket{1}_B) = \ket{0}_A\ket{0}_A\ket{\psi}_B \\ 01 &\to \ket{0}_A\ket{1}_A(\alpha\ket{1}_B + \beta\ket{0}_B) = \ket{0}_A\ket{1}_A(X\ket{\psi})_B \\ 10 &\to \ket{1}_A\ket{0}_A(\alpha\ket{0}_B - \beta\ket{1}_B) = \ket{0}_A\ket{0}_A(Z\ket{\psi})_B \\ 11 &\to \ket{1}_A\ket{1}_A(\alpha\ket{1}_B - \beta\ket{0}_B) = \ket{0}_A\ket{0}_A(XZ\ket{\psi})_B \end{align} この式を見れば、最後に測定結果に応じて \(X, Z\) ゲートをかけることで \(\ket{\psi}\) という量子状態を B さんが受け取れることが一目瞭然かと思う。5. ベル測定
実はここで使われた CNOT ゲート + H ゲート + 測定というシーケンスは、ベル測定
と呼ばれている。CNOT + H ゲートは、ベル状態
とかベル基底
と呼ばれる最大にエンタングルした 4 つの状態 \begin{align} \ket{\Phi_0} &= \frac{\ket{00}+\ket{11}}{\sqrt{2}}\\ \ket{\Phi_1} &= \frac{\ket{01}+\ket{10}}{\sqrt{2}}\\ \ket{\Phi_2} &= \frac{\ket{00}-\ket{11}}{\sqrt{2}}\\ \ket{\Phi_3} &= \frac{\ket{01}-\ket{10}}{\sqrt{2}} \end{align} をそれぞれ \begin{align} \ket{\Phi_0} &\to \ket{00}\\ \ket{\Phi_1} &\to \ket{01}\\ \ket{\Phi_2} &\to \ket{10}\\ \ket{\Phi_3} &\to \ket{11} \end{align} に変換する働きがある。したがって、CNOT ゲート + H ゲート + 測定 というシーケンスは結局のところ、\(\ket{\Phi_i}\) に対する射影測定をしていることになる。そこで初期状態の A さん側を \(\ket{\Phi_i}\) で展開してみると、 \begin{align} &\frac{1}{\sqrt{2}}(\alpha\ket{0}_A+\beta\ket{1}_A) \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right)\\ &=\frac{1}{2}\ket{\Phi_0}_A(\alpha\ket{0}_B + \beta\ket{1}_B) \\ &+\frac{1}{2}\ket{\Phi_1}_A(\alpha\ket{1}_B + \beta\ket{0}_B) \\ &+\frac{1}{2}\ket{\Phi_2}_A(\alpha\ket{0}_B - \beta\ket{1}_B) \\ &+\frac{1}{2}\ket{\Phi_3}_A(\alpha\ket{1}_B - \beta\ket{0}_B) \end{align} となっており、確かにこのベル基底に対して射影測定をすればテレポーテーションが起きることがわかるだろう。
5. 一般の最大エンタングル状態を使ったテレポーテーション
以上では \begin{align} \frac{1}{\sqrt{2}} \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right) \end{align} というエンタングル状態を使ってテレポーテーションを行った。これは最大にエンタングルした状態である。最大にエンタングルした量子状態はこれだけではないが、他の量子状態を使っても同じことができるだろうか?そこでここでは、\(N\) 次元の最大エンタングル状態 \begin{align} \ket{\Phi^{AB}} = \frac{1}{\sqrt{N}}\sum_{i=0}^{N-1} \ket{i}_A\ket{i}_B \end{align} を使ったテレポーテーションを考えてみよう。テレポートさせたい状態も \(N\) 次元の量子状態 \begin{align} \ket{\psi} = \sum_{i=0}^{N-1} a_i \ket{i} \end{align} であるとする。したがって、初期状態は \begin{align} \left(\sum_{i=0}^{N-1} a_i \ket{i}_A\right)\left(\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \ket{j}_A\ket{j}_B\right) \end{align} である。
少し天下り的だが、N 次元の 2 つの量子系が最大にエンタングルした状態は、 \begin{align} \ket{\Phi_{nm}} = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} e^{i2\pi nj/N}\ket{j+m~\mathrm{mod}~N}\ket{j} \end{align} とかける。ただし \(n,m\) は \(0\leq n,m \lt N\) の整数である。この \(\ket{\Phi_{nm}}\) によって A さんの持つ初期状態を展開してみよう。
まず、 \begin{align} \ket{\Phi_{nm}} = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} e^{i2\pi nj/N}\ket{j+m~\mathrm{mod}~N}\ket{j} \end{align} の式を逆に \(\ket{j+m~\mathrm{mod}~N}\ket{j}=\) の形にする。これには離散フーリエ変換と同じように、両辺に \(e^{-i2\pi nk/N}/\sqrt{N}\) をかけて \(n\) に関する和を取ればよくて、 \begin{align} \ket{k+m~\mathrm{mod}~N}\ket{k} = \frac{1}{\sqrt{N}}\sum_{n=0}^{N-1} e^{-i2\pi nk/N} \ket{\Phi_{nm}} \end{align} となる。この式を初期状態へと代入するが \begin{align} &\left(\sum_{i=0}^{N-1} a_i \ket{i}_A\right)\left(\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \ket{j}_A\ket{j}_B\right)\\ &=\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \sum_{i=0}^{N-1} a_i \ket{i}_A \ket{j}_A\ket{j}_B \\ &=\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \sum_{m=0}^{N-1} a_{j+m~\mathrm{mod}~N} \ket{j+m~\mathrm{mod}~N}_A \ket{j}_A\ket{j}_B \end{align} に注意して、 \begin{align} &=\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \sum_{m=0}^{N-1} a_{j+m~\mathrm{mod}~N} \left(\frac{1}{\sqrt{N}}\sum_{n=0}^{N-1} e^{-i2\pi nj/N} \ket{\Phi_{nm}}\right)\ket{j}_B \\ &=\frac{1}{N}\sum_{j=0}^{N-1} \sum_{m=0}^{N-1}\sum_{n=0}^{N-1} a_{j+m~\mathrm{mod}~N} e^{-i2\pi nj/N} \ket{\Phi_{nm}} \ket{j}_B \\ &=\frac{1}{N}\sum_{j=0}^{N-1} \left(\sum_{m=0}^{N-1} \sum_{n=0}^{N-1} a_{j+m~\mathrm{mod}~N} e^{-i2\pi nj/N}\ket{\Phi_{nm}}\right) \ket{j}_B \\ \end{align} を得る。
さて、A さんが \(\ket{\Phi_{nm}}\) に対する射影測定を行って、\(\ket{\Phi_{n_0 m_0}}\) という結果を得たとする。このとき B さんには \begin{align} \frac{1}{N}\sum_{j=0}^{N-1} a_{j+m_0~\mathrm{mod}~N} e^{-i2\pi n_0 j/N} \ket{j}_B \\ \end{align} という状態が残される。1 qubit の量子テレポーテーションと同様に、A さんが B さんに \(n_0, m_0\) という情報を渡していれば、B さんはその情報をもとに、 \begin{align} &\frac{1}{N}\sum_{j=0}^{N-1} a_{j+m_0~\mathrm{mod}~N} e^{-i2\pi n_0 j/N} \ket{j}_B \\ &\to \frac{1}{N}\sum_{j=0}^{N-1} a_{j} \ket{j}_B \end{align} という変換ができるだろう。これで一般の最大にエンタングルした状態を用いても、量子テレポーテーションを行えることがわかった。
最大エンタングル状態 \(\ket{\Phi_{nm}}\) の構成については C.H. Bennett, et al. PRL 70, 1895 (1993) を参考にした。