理想気体の熱容量
1.理想気体のCv
今回は理想気体の変化の様子を中心に調べていこう。ちなみに理想気体とは、その状態が\[ pV = nRT \] で完璧に表すことのできる気体のことだった。現実の気体も希薄状態ならば十分この方程式にしたがって変化していると考えても いいらしい。希薄でない状態の気体に関しては、次回に考えることにしよう。さて、nというのは考えている気体のモル数 を表しているわけだが、nが式に入っていると少しうっとうしいので、とりあえず今回はn=1[mol]として考えることにする。え、 勝手にそんなことしていいの?と思うかもしれないが、気体分子の量を決めるだけなので、別に問題ない。注意するのは、この 仮定の下で出てくるCvは
定積モル比熱
になるということだけだ。定積モル比熱っちゃなんだという話になるが、何のことはない、 1[mol]あたりの定積熱容量のことだ。もし気体がn[mol]あれば、その気体の定積熱容量はnCvということになる。ともかく、n=1[mol]とすると、状態方程式は\(pV=RT\)になる。
さて、Cvを求めていこう。Cvは式でどうやって表されていたかというと、
\[ C_v = \left(\frac{\partial U}{\partial T}\right)_V \] こうだった。つまり、理想気体の内部エネルギーが何とかしてp,T,Vなどで表されればよいわけだ。 しかし、これをやるには統計力学の世界に一歩踏み込まないといけない。熱力学の世界から外れるのは あんまり気乗りはしないがやるしかしょうがないからやっていこう。
さて、下のような立方体に入った単原子分子の理想気体について考える。
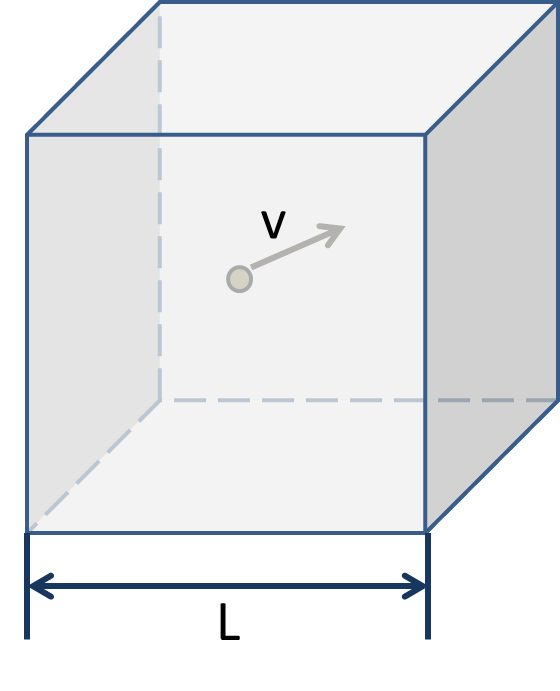
まずx方向への速度を\(v_x\)とすれば、分子がx方向に往復するのにかかる時間\(\Delta t\)は\(\Delta t=\frac{L}{v_x}\)となる。
さらに衝突時分子の運動量変化は、分子の質量をmとして\(2mv_x\)とかけるだろう。
これが\(\Delta t\)間に壁が受ける力積に 等しいわけだから、平均して壁が分子から受ける力\(F\)は
\[F=\frac{2mv_x}{\Delta t}=\frac{2mv_x^2}{L}\] という具合になる。 これから壁に加わる圧力を計算すれば、
\[p=N\frac{F}{L^2}=N\frac{2mv_x^2}{L^3}=N\frac{2mv_x^2}{V}\] とできる。Nというのは気体分子の数である。さらに、分子の速度がx,y,z方向に均等に分散しているとすれば(\(v_x=v_y=v_z\))、分子の速さ\(v\)は
\[v^2 = v_x^2+v_y^2+v_z^2 = 3v_x^2\] となる。分子というのはものすごい数あるわけだから、別にこの仮定も平均的に見ればおかしくはないだろう。 とにかく、これによって、
\[pV = N\frac{2}{3}mv^2\] が得られる。あとはこれを内部エネルギーUと結びつけられればよい。Uというのはこの場合分子の運動エネルギーを全て足し合わせ たものと考えれば、\(U=\frac{1}{2}mv^2N\)とできるから、これをつかって
\[U = \frac{3}{2}pV = \frac{3}{2}RT\] とUを表すことができた。
ただしこれは単原子分子の場合だけであり、多原子分子の場合には、回転による運動エネルギーも考慮しなければならない。ちなみに 軸対称な多原子分子の場合には\(U=\frac{5}{2}RT\)、対称でない多原子分子については、\(U=3RT\)が得られる。
さて、ちょっとわき道にそれてしまったが、これでやっと理想気体のCvが求められる。
\[ C_v = \left(\frac{\partial U}{\partial T}\right)_V = \frac{3}{2}R \] ということだ。(単原子分子の場合)
2.理想気体のCp
Cvを出せたのだから、Cpも出したいというのが自然だろう。CpとCvの間に成り立つ関係式を思い出そう。\[C_p - C_v = \left\{ p + \left(\frac {\partial U}{\partial V}\right)_T \right\} \left(\frac {\partial V}{\partial T}\right)_p\] これに\(U=\frac{3}{2}RT\)と\(V=\frac{RT}{p}\)を代入してやる。計算というほどの計算ではないが、計算すると、
\[C_p - C_v = R\] とまたなかなかきれいな式が出てくる。この式は理想気体ならばどんな気体であっても成り立つことが分かる。なぜなら 理想気体の内部エネルギーはさっき見たように、温度にのみ依存するからだ。 この式を使ってやればCpはCvから簡単に出すことができて、
\[C_p = \frac{5}{2}R \] になる。いちおう断っておくが、これも単原子分子の場合である。