量子誤り訂正の基礎 - 多数決符号
量子誤り訂正
量子誤り訂正とは、非常にもろく、壊れやすい「量子状態」を保護するための技術である。特に量子ビットの状態に対する誤り訂正の実現は、量子コンピュータを作るのに必須であり、その文脈で触れられることが多い。個人的には、様々な量子状態の「量子性」が保たれる時間を、外部からの操作によって (一定の条件さえ満たされればほとんど無制限に) 伸ばせるという事自体がとてもおもしろいと思う。この記事では最も単純な符号である多数決符号を題材に、量子誤り訂正のエッセンスを説明したい。
基本的な量子ゲートを知っている、くらいのレベルを想定した説明をする。(古典誤り訂正の知識は求めない。)
多数決符号
多数決符号は、古典的な誤り訂正においても最も簡単な符号の一つである。説明のため、あるビット \(b \in \{0,1\}\) を誰かに送りたい、あるいは長い時間その情報を保持したいという状況を考えよう。このとき、例えば電磁波やコンデンサの電荷としてエンコードされた、一つの物理的なビット情報は、単位時間当たり \(p\) の確率で \(0\to 1\) あるいは \(1\to 0\) と反転してしまうとする。このような状況下で情報を守るための最も簡単なアイデアが多数決符号である。多数決符号では、保持したい情報である \(0\) を、たくさんの物理ビットを使って \(00\cdots 0\) と表し、逆に \(1\) を \(11\cdots 1\) と表すと約束することにより、誤りの抑制を図る。どれかのビットに誤りが起きたとしても、\(0\) か \(1\) の多い方をもとの情報だと考えれば、元の情報を復元できるだろう。ビット反転エラーが独立に起こるとすれば、半分以上のビットが反転してしまう確率は非常に低いからである。
このとき、\(00\cdots 0\) や \(11\cdots 1\) で表される \(0\) や \(1\) という情報のことを 論理ビット と呼ぶ。逆に、論理ビットを構成している物理的な個々のビットのことを物理ビットと呼ぶ。
「量子」誤り訂正符号に要求したいこと
多数決符号を量子ビットの保護へと拡張したい。簡単のため、ここからは 3 ビットだけを考えることにしよう。3ビットの多数決符号の論理ビット \(0_L\), \(1_L\) は、 \begin{align} 0_L &= (000) \\ 1_L &= (111) \end{align} と表せる。これを素直に拡張するなら、物理的な量子ビットを 3 つ使って、1 つの論理量子ビット \(\ket{0}_L\), \(\ket{1}_L\) を \begin{align} \ket{0}_L &:= \ket{000} \\ \ket{1}_L &:= \ket{111} \end{align} と定義すればよさそうな気がする。このような論理量子ビットを使えば、古典的なビットの誤り訂正と同じように、「量子」誤り訂正もできるのだろうか?そのことをしっかり考えるために、「量子」誤り訂正に要求したいことを明確にしておきたい。普通量子状態の誤り訂正をしたい、といったときには、\(\ket{0}_L\) や \(\ket{1}_L\) に対する誤りを訂正し保持しておけるだけでは不十分で、より一般に \begin{align} \alpha \ket{0}_L + \beta \ket{1}_L \end{align} のような重ね合わせ状態をも保存しておけなければ意味がない。\(\ket{0}_L\) や \(\ket{1}_L\) を保存するだけで十分ならば、なにも量子ビットを使う必要はなくて、古典ビットを使えばよいのだから。
古典誤り訂正との違い
さて、上のように構成した \(\ket{0}_L\) と \(\ket{1}_L\) で、重ね合わせ状態も含めて誤り訂正を実行したい。古典ビットの場合には、物理ビットに含まれる \(0\) と \(1\) の数を数えて、多いほうが論理ビットの表す情報であると結論すればよかった。しかし量子ビットの場合には、もし \(0\) と \(1\) の数を数えようと物理量子ビットを測定してしまうと、物理量子ビットはすべて \(0\) か \(1\) に収束してしまう。もし元の状態が \(\alpha\ket{0}_L + \beta \ket{1}_L\) だったとしたら、もともとは誤りを訂正するために行っていた測定操作によって、\(\ket{000}=\ket{0}_L\) もしくは \(\ket{111}=\ket{1}_L\) へと状態を壊すことになる。もちろん、もし測定結果から \(\alpha, \beta\) を推定できるのなら元の状態を復元できるが、この測定結果から係数を推定することは不可能だろう。したがって、古典的な多数決符号と同じ戦略 (ビットの数を数える手法) をとっていては、多数決符号をそのまま量子状態の誤り訂正に応用することはできない。
間接的に量子ビットの情報を知る
0, 1 の数を数えるという方針では誤り訂正を行えないことがわかったので、別の方法を考えなければいけない。実はうまく行く方法として、隣同士の物理ビットが同じか同じでないか (=ビット間のパリティ) を調べて、実効的に同じ情報を得る方法がある。以下に隣同士のビット間のパリティを表にしてみた。\(\oplus\) は XOR で、ビットが同じ場合0を、違う場合1を返す演算である。
| 物理ビットの値 \((b_1b_2b_3)\) | \(b_1\oplus b_2\) | \(b_2\oplus b_3\) |
| 000 | 0 | 0 |
| 001 | 0 | 1 |
| 010 | 1 | 1 |
| 011 | 1 | 0 |
| 100 | 1 | 0 |
| 101 | 1 | 1 |
| 110 | 0 | 1 |
| 111 | 0 | 0 |
| \(b_1\oplus b_2\) | \(b_2\oplus b_3\) | 誤りの発生したビット |
| 0 | 0 | - |
| 0 | 1 | \(b_3\) |
| 1 | 1 | \(b_2\) |
| 1 | 0 | \(b_1\) |
パリティの間接検出
パリティを検出しても多数決符号による訂正ができることがわかったが、パリティの計算を 3 つの物理量子ビットを直接測定してしまっては元の木阿弥だ。実は以下のように (\(\ket{0}\)に初期化した) 補助的な量子ビットを使って、パリティを間接的に検出すればこの問題を解決できる。
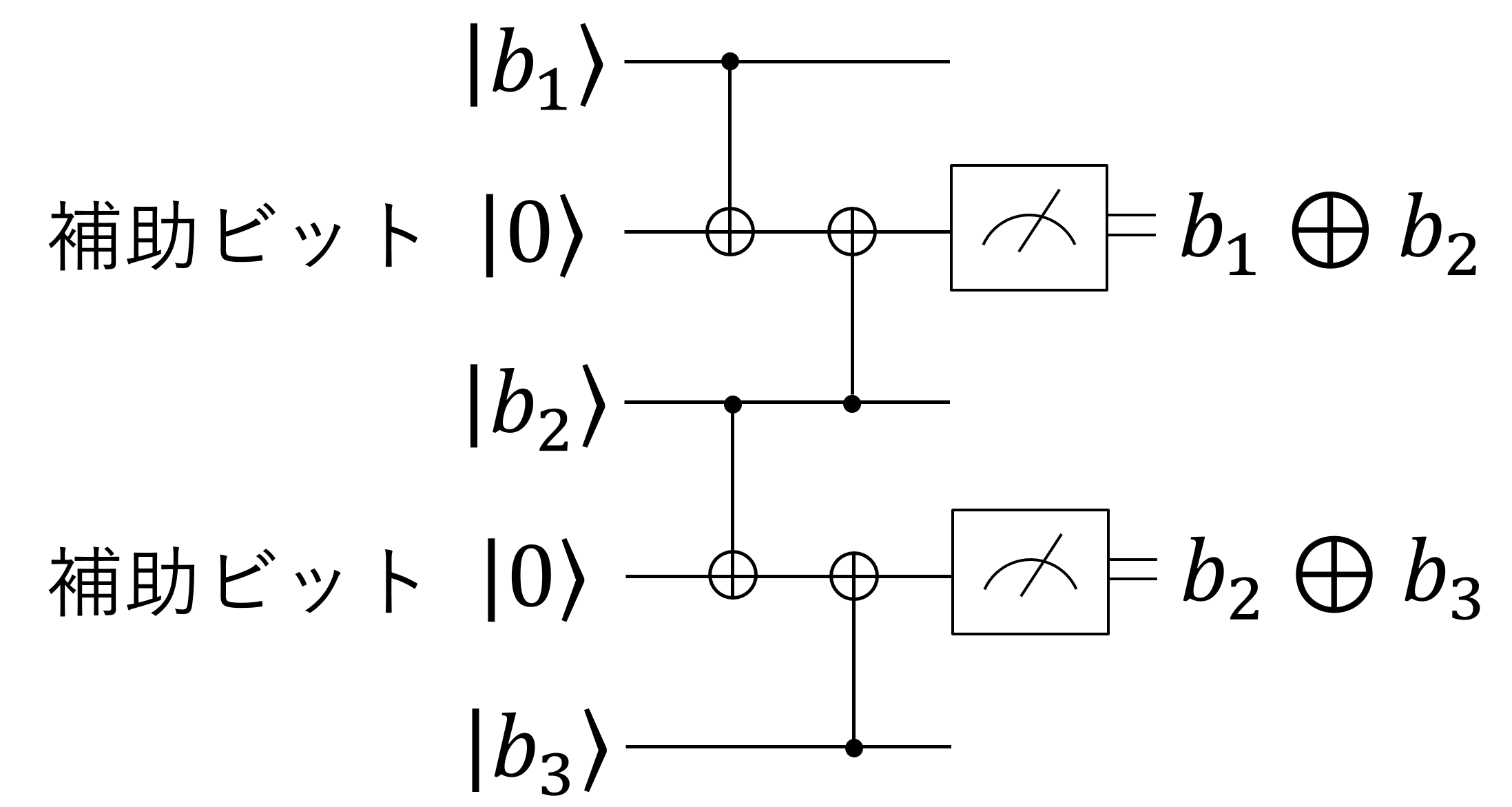
誤り検出の特性
最後に、上の回路に色々な入力状態を入れてみて、その特性を調べてみよう。1つの物理ビットが反転した状態
- 論理量子ビット \(\alpha\ket{000}_{123} + \beta \ket{111}_{123}\) の2番目の物理ビットが何らかの原因によって反転してしまった状態、つまり \(\alpha\ket{010}_{123} + \beta \ket{101}_{123}\) を回路に入力する。このとき補助量子ビットは \(\ket{1}_{p_{12}}\ket{1}_{p_{23}}\) になり、必ず 11 が測定される。上の表を見れば 11 は 2 番目の物理量子ビットにエラーが起きていることに対応すると分かるので、2番目の物理量子ビットを反転させれば、元の状態に戻せる。1, 3 番目のビットにビット反転エラーが起きた場合も同様である。
1つの物理ビットが微妙に反転した状態
-
上のように完全に反転するまではいかないが、ある角度 \(\theta\) だけ2番目の量子ビットが反転してしまった状態
\begin{align}
\cos \theta (\alpha\ket{000}_{123} + \beta \ket{111}_{123}) + \sin \theta (\alpha\ket{010}_{123} + \beta \ket{101}_{123})
\end{align}
を入力してみよう。補助量子ビットは、\(\cos\theta\) がついている項については \(\ket{0}_{p_{12}}\ket{0}_{p_{23}}\) となり、\(\sin\theta\) がついている項については \(\ket{1}_{p_{12}}\ket{1}_{p_{23}}\) となることがわかると思う。したがって、補助量子ビットの測定直前では
\begin{align}
\cos \theta (\alpha\ket{000}_{123} + \beta \ket{111}_{123})\ket{0}_{p_{12}}\ket{0}_{p_{23}} + \sin \theta (\alpha\ket{010}_{123} + \beta \ket{101}_{123}) \ket{1}_{p_{12}}\ket{1}_{p_{23}}
\end{align}
という状態になる。この状態の補助量子ビットを測定すると、\(\cos^2\theta\) の確率で 00 が、\(\sin^2\theta\) の確率で 11 が観測されるだろう。そして測定後の状態は
\begin{align}
\text{測定結果が 00} &\to (\alpha\ket{000}_{123} + \beta \ket{111}_{123})\ket{0}_{p_{12}}\ket{0}_{p_{23}} \\
\text{測定結果が 11} &\to (\alpha\ket{010}_{123} + \beta \ket{101}_{123}) \ket{1}_{p_{12}}\ket{1}_{p_{23}}
\end{align}
にそれぞれ収束する。上の式を見ればわかるように、測定結果が 00 の場合には元の状態へと「勝手に」復元されて、測定結果が 11 の場合には、2 番目の物理ビットにビット反転エラーがかかった量子状態になる。したがって、11 のときには先程見た例と全く同様に、2 番目の物理ビットを反転させてあげれば、元の量子状態を復元できる。つまりこのプロトコルはこのようなエラーも訂正できる。
式だけだと狐につままれたような気分になる人もいるかも知れないので補足。ある角度だけ反転してしまったようなエラーは、ある意味「2番目のビットが反転していない世界」と「2番目のビットが反転してしまった世界」の重ね合わせ状態を生み出す、といってもいい。そこで 2 番目のビットが反転しているかいないかを「測定」すると、量子力学の原理から、世界は必ずどちらかのケースに収縮する。そうすると、僕たちはその世界でうまくいくように復元すればよいことになる。個人的には、世の中うまくできているものだ、と感心した。
位相エラー
- \(\alpha\ket{000}_{123} + \beta \ket{111}_{123}\) に用意した論理量子ビットが、 \begin{align} \alpha\ket{000}_{123} + e^{i\theta}\beta \ket{111}_{123} \end{align} のように変化してしまった場合を考えよう。この場合補助量子ビットは必ず 00 になるので、誤りを検知することすらできない。
まとめ
今回は多数決符号を例に、量子誤り訂正の構成方法について書いてみた。この例が伝える量子誤り訂正のエッセンスは次のような感じ。(だと思う。)-
論理量子ビットの状態を壊さないように、補助量子ビットを用いた測定が必要となる。
- 半端に反転したようなエラーも、補助量子ビットの測定によって、反転している・いない世界のどちらかに収縮させることで、復元可能になる。(このような半端なエラーのことを、コヒーレントエラーと呼ぶ。)
- ビットの反転だけでなく、量子状態の係数の変化 (上の位相エラーのようなエラー) にも対応できるような誤り訂正手法が必要である。