量子計算におけるゲート色々
1.ゲートとは
量子コンピュータを学んでみたいと思っている方は、多分古典的なコンピュータで基本的な構成要素となるロジックゲート
についてはもう知っているかと思いますが、一応簡単にまとめておきます。それから量子コンピュータにおけるゲート操作の話をしましょう。ロジックゲートには、
ANDゲート、ORゲート、NOTゲート
などがあります。例えばANDゲートは下の図のように書かれることが多いでしょう。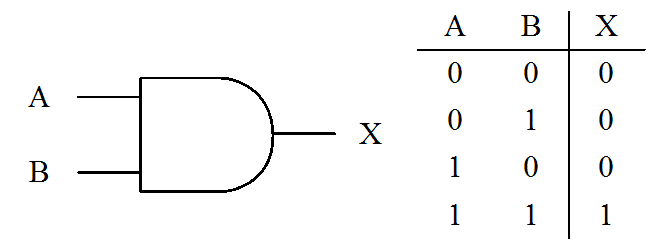
量子コンピュータにおいても、同じように様々なゲートをうまいこと組み合わせることで、色々な計算を行うことができます。そこで今回は量子コンピュータにおけるゲートの概念を紹介したいと思います。
ただし、まだまだできることが狭いのが現実ですが。でもきっと、これから頭のいい人達がすごい回路を考えてくれるでしょう。
2.1qubit量子ゲートの例
古典コンピュータでの論理ゲートについておさらいしたところで、ここからは量子コンピュータでのゲートに関して話していきます。NOTゲート (Xゲート)
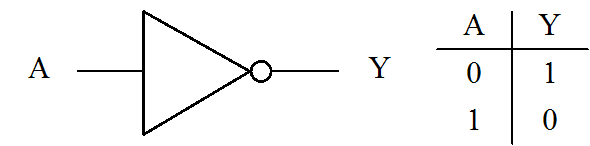
古典コンピュータでのNOTゲートは1を0に、0を1にするものでした。当然ながら、量子コンピュータでもNOTゲートがあります。図を下に書いてみましたが、全然書く必要も無いくらいですね。このゲートは\(\ket{0}\)を\(\ket{1}\)に、\(\ket{1}\)を\(\ket{0}\)に変換します。量子コンピュータの世界では普通
Xゲート
と呼ばれます。この名前の付け方には、まあ色々わけがあるのです。説明すると長くなるので今回詳しくは書きませんが、スピンの量子力学を知っている人ならその意味がわかるかもしれません。
アダマール (Hadamard) ゲート
さっきのNOTゲートは古典コンピュータと同じで全然おもしろくなかったですね。ここからが量子コンピュータ特有のゲートの話の始まりです。
Hadamardゲート
は、\(\ket{0}\)を\(\ket{0},\ket{1}\)が同じ大きさで、重ね合わさった状態にするゲートのことです。具体的には下のように変換します。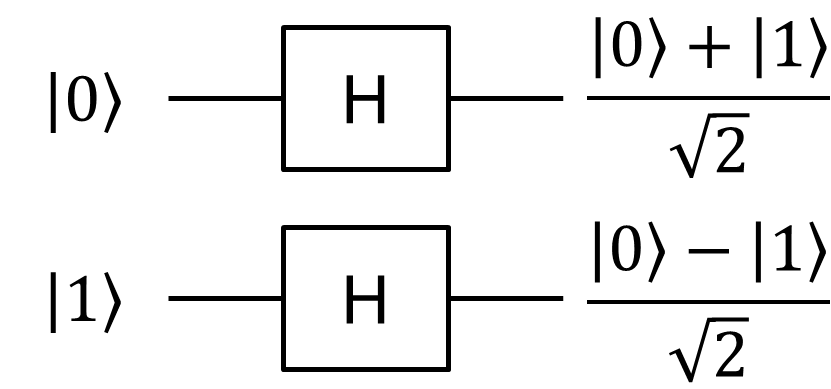
位相ゲート
位相ゲートは、\(\ket{0}\)と\(\ket{1}\)の間の位相差を変化させるゲートです。例えば位相差\(\phi\)をつける位相ゲートに、先程のアダマールゲートで作った重ね合わせ状態を通してあげると、 \begin{align} \frac{\ket{0}+\ket{1}}{\sqrt{2}}&\to\frac{\ket{0}+e^{i\phi}\ket{1}}{\sqrt{2}}\\ \frac{\ket{0}-\ket{1}}{\sqrt{2}}&\to\frac{\ket{0}-e^{i\phi}\ket{1}}{\sqrt{2}} \end{align} と変化します。\(\ket{0}\)をそのままに、\(\ket{1}\to e^{i\phi}\ket{1}\)という変換をするゲートです。
1qubitのゲートはこれくらいにしておいて、次は2qubitゲートについて紹介しましょう。
3.2qubit量子ゲートの例
ここまでは1qubitに対するゲートの例を紹介しました。しかし、古典コンピュータでANDゲートのように2bitを入力としてとるものがあったように、量子コンピュータでも2qubitゲートがあります。今回はその例を1つだけ紹介しましょう。Controlled-NOT (C-NOT) ゲート
C-NOTゲートは、片方(Control qubit)のqubitが1ならもう一つのqubitを反転させるという働きをします。図は下のように書かれることが多いです。
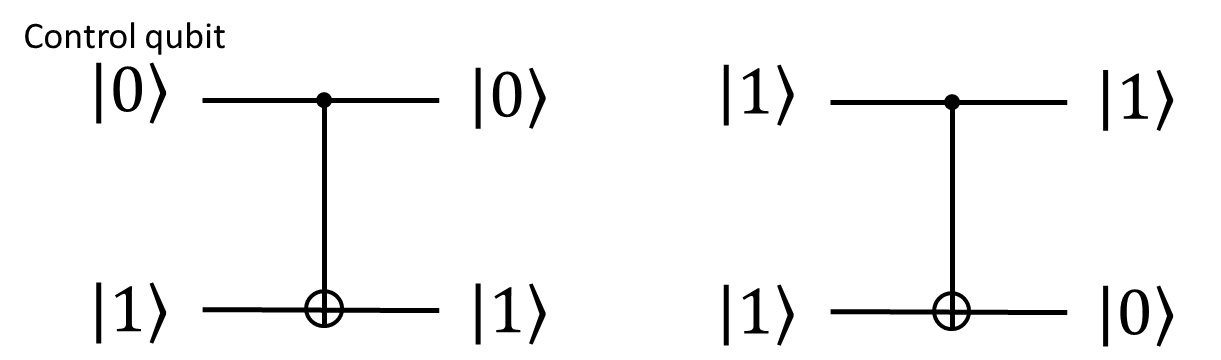
量子コンピュータを一般向けに紹介する記事のほとんどで、量子コンピュータを使うと
超並列処理
が可能になる、と言われますが、その意味をこのゲートから少しだけ垣間見ることができます。例えばC-NOTゲートを重ね合わせ状態 \[\frac{3}{5}\ket{0}+\frac{4}{5}\ket{1}\] をcontrol bitとして作用させて見ましょう。(一応補足しておくと、この状態は、9/25の確率で0を、16/25の確率で1を観測するような状態です。まだこの確率をどうやって求めるかは解説していないですが、とりあえずはまあそんなものだと思ってください。) どのようになるでしょうか。答えは下の図です。
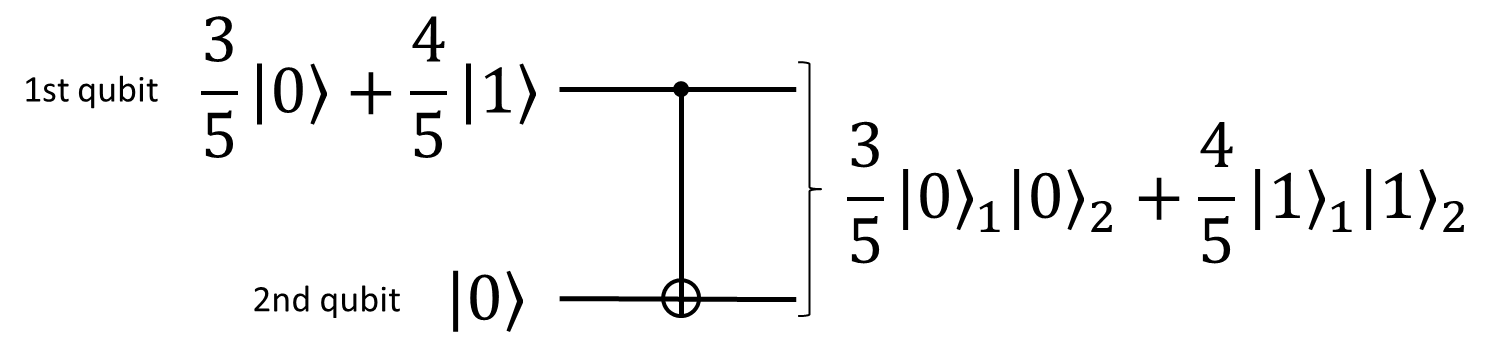
この状態に対して、C-NOTゲートを作用させると、重ね合わせの第一項目\(\ket{0}_1\ket{0}_2\)については、C-NOTゲートは何もしません。なぜなら、この状態のcontrol bitは\(\ket{0}\)だからです。一方で、第二項目\(\ket{1}_1\ket{0}_2\)について考えると、この状態のcontrol bitは\(\ket{1}\)なので、こちらの状態については2番目のqubitを反転させます。だからC-NOTゲートを通すと、\(\ket{1}_1\ket{0}_2\)という状態は\(\ket{1}_1\ket{1}_2\)に移ります。したがって、全体では、 \[\left(\frac{3}{5}\ket{0}_1+\frac{4}{5}\ket{1}_1\right)\ket{0}_2\to\frac{3}{5}\ket{0}_1\ket{0}_2+\frac{4}{5}\ket{1}_1\ket{1}_2\] という変換が行われることになります。
C-NOTゲートを使うことによって、多数の重ね合わせ状態を並列に処理できることがわかってもらえたでしょうか。このようなゲートはC-NOTゲートだけではなく、もっと一般に、任意の1qubitゲートUをcontrol bitの状態に応じて実行するような、controlled-Uゲートを作れることが知られています。このようなcontrolledゲートが量子コンピュータで重要な役割を果たすのです。
4.ゲートの物理的実装
ここまで色々なゲートを紹介しましたが、qubitに対する操作がどのように行われるのか知らないと気持ち悪い! という人もいるでしょう。(私もその1人でした。) そこで簡単な説明をしておきます。電子や核スピンを用いる方法と、今主流の超電導量子bitを用いる方法では、そのqubitのエネルギー準位差に等しい振動数の電磁波を照射することでqubitを操作します。そのような振動数の電磁波をある一定時間照射すると、\(\ket{0}\)を\(\ket{1}\)に、\(\ket{1}\)を\(\ket{0}\)に反転させることができるのです。さらにそれだけではなく、その半分の時間照射すれば、\(\ket{0}\)を重ね合わせ状態\((\ket{0}+\ket{1})/\sqrt{2}\)へ持っていったりできます。詳しい物理を知りたい人は二準位系とラビ振動のページを参照。
2qubitゲートなどもっと詳しい説明をしようとすると長くなってしまうので、今回はこのあたりで終わっておきますが、電磁波をうまいこと作り出して操作をするという概念は2qubitでも同じです。そのうち解説したいと思います。
でも、量子コンピュータで何ができるのか、ということを純粋に知りたいだけの人は、そんなことを詳細に知る必要はありません。ちょうど、パソコンのCPUでCMOSトランジスタがどのように動いているのか、プログラマは知らなくても良いのと同じことです。