量子コンピュータのための量子力学の基礎
0.今回の記事の読み方
量子力学で「原理」とされていることをまとめた記事になります。ここに書いてあることは、量子コンピュータを説明する上で避けては通れないものです。「原理」なので、なるべく理由を求めずに、暗記してしまうほうがいいと思います。なぜこんな原理に落ち着いたのかという理由を知りたい人は、このサイトの量子力学index全部読むくらいの気持ちが必要です。てっとり早く量子コンピュータを知りたい!という人はここに書いてあることは全部認めてしまいましょう。1.状態と確率
qubitには\(\ket{0}\)と\(\ket{1}\)という2つの状態があり、そしてこれはちょうど、スピン1/2の粒子のスピンの向き (z軸方向上向き・下向き) に対応しているのでした。しかし、qubitが取れる状態はその2つだけではありません。古典コンピュータにおけるbitは0,1の2つの値しか取れませんが、量子コンピュータにおけるqubitにはさらに \[\frac{\ket{0}+\ket{1}}{\sqrt{2}}\] のように\(\ket{0}\)と\(\ket{1}\)を重ね合わせた状態をとることができます。
さて、ではqubitの一般的な状態は、つまり一般的な重ね合わせのやり方は、 \[\ket{\psi} = \alpha\ket{0}+\beta\ket{1}\tag{1}\] と表すことができます。(あ、\(\psi\)はプサイと読みます。量子力学で適当な状態を表すときによく使う記号です。)
この状態\(\ket{\psi}\)の物理的意味は、このqubitを観測したときの確率として現れます。具体的には、\(\ket{\psi}\)を観測したとき、このqubitがz軸に対して上向き (つまり\(\ket{0}\)) として観測される確率は\(|\alpha|^2\)であり、逆に下向き\(\ket{1}\)として観測される確率は\(|\beta|^2\)です。式で書くなら、 \[P(\ket{0}) = |\alpha|^2, P(\ket{1}) = |\beta|^2\] とでも書けばいいでしょう。
ポイントは、
係数の絶対値の二乗
がその状態が観測される確率を表すというところです。2.状態はベクトルだ!
実は、状態\(\ket{0}\)や\(\ket{1}\)は、大きさが1で互いに直交するベクトルです。何を言っているのか意味がわからないかもしれませんが、認めてもらうしかありません。\(\ket{0}\)と\(\ket{1}\)はそれぞれ、x方向の単位ベクトル\(\b{e}_x\)とy方向の単位ベクトル\(\b{e}_y\)と全く同じような性質を持つということです。なぜこんな事になっているかということを説明するには、量子力学の深ーい歴史について話さないといけないのです。とにかく、昔の天才たちがスピンという現象を説明するために話し合った結果、こう考えると都合がいい、ということで話がまとまったのです。
ベクトルなのですから、ベクトル同士の内積ということも考えたいですね。さっきの単位ベクトル\(\b{e}_x\)の内積は、例えば \[\b{e}_x^T\b{e}_x=1, \b{e}_x^T\b{e}_y=0\] のように書かれます。Tは転置を表します。最初の式は\(\b{e}_x\)の大きさが1であることを、2番目の式は\(\b{e}_x,\b{e}_y\)が直交していることを示すものです。複素数のベクトルを考えるときには、 \[\b{e}_x^\dagger\b{e}_x=1, \b{e}_x^\dagger\b{e}_y=0\] とします。\(\dagger\) (ダガー) は転置をとって、さらに複素共役をとるという記号です。さて、量子力学のベクトル\(\ket{0},\ket{1}\)について、内積をどのように書くのか説明していきます。量子力学では、\(\ket{0}\)にダガーを掛けたものを次のように書きます。 \[\ket{0}^\dagger = \bra{0}\] \(\bra{0}\)はブラ0と読みます。括弧の向きを反転させるだけです。ということで、内積は次のように書きます。 \[\ket{0}^\dagger\ket{0} = \bra{0}\ket{0}\] ただ、真ん中の線を1つ省略してしまって、 \[\ket{0}^\dagger\ket{0} = \braket{0}{0}\] と書くことが多いです。
3.演算子と固有状態
なんだか難しい言葉がたくさん出てきました。演算子なんて聞くのも嫌だ、という人もいるでしょう。でも量子力学を語る上では避けて通れない言葉なのです。でも、量子コンピュータに限った話なら、演算子という言葉は簡単な「行列」という言葉に置き換えることができるので、そういう方向性で話を進めたいと思います。さて、それにはまず1qubitの一般的な状態\(\ket{\psi}\)をさっきのことを踏まえて、ベクトルとして捉え直さないと始まりません。実は、(1)式にも書いた、 \[\ket{\psi} = \alpha\ket{0}+\beta\ket{1}\tag{1}\] という状態は、\(\ket{0}\)と\(\ket{1}\)という状態を基底ベクトルだと思って、次のようなよくあるベクトルの形に書き直せます。 \[\ket{\psi} \dot{=} \left(\begin{array}{c}\alpha\\\beta\end{array}\right)\] こういう書き方をした時、自分で暗にルールを設定していることに注意しましょう。どのようなルールかというと、「1番目の成分が\(\ket{0}\)に掛かって、2番目の成分が\(\ket{1}\)に掛かる」というルールです。
さて、量子コンピュータにおいて1qubitに対する演算子\(A\)は次のように2x2の行列で表します。 \[A=\left(\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array} \right)\] 例を挙げてみると、例えば前回紹介したX (NOT) ゲートやHadamardゲートは次のように書かれる演算子です。 \[X=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)\] \[H=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}0&1\\1&0\end{array}\right)\] 例えばXゲートがどういうことをするのかみてみるために、\(\ket{\psi}=\alpha\ket{0}+\beta\ket{1}\)にかけてみましょう。すると、 \[X\ket{\psi} = \left(\begin{array}{cc}0&1\\1&0\end{array}\right)\left(\begin{array}{c}\alpha\\\beta\end{array}\right) = \left(\begin{array}{c}\beta\\\alpha\end{array}\right)\] となって、確かにNOTゲートの働き、すなわち\(\alpha,\beta\)を入れ替える働きをしていることがわかります。
さて、行列といえば、
固有ベクトル
というのが重要でしたね。ある行列\(A\)に対する固有ベクトル\(\b{x}\)とはどういう性質を持つものだったか覚えているでしょうか?それは、 \[A\b{x} = a\b{x}\] のように、行列Aを掛けてもある定数\(a\)倍されるだけで、向きが変わらないベクトルのことでした。この\(a\)のことを固有値
と呼びます。量子力学でこの固有ベクトルという概念はとっても大事です。ただし、量子力学では、この固有ベクトルのことが
固有状態
と呼ばれることもあります。4.観測と固有値と固有状態
これまで、\(\ket{0}\)と\(\ket{1}\)をqubitとして考えてきました。この2つの状態は物理的にどういう意味だったのかというと、スピンのz方向がそれぞれ下向き、上向きとなっている状態を表しているのでした。しかし、良く考えてみれば、x方向やy方向に対して上向きか下向きか、ということでqubitを表現することもできるはずでしょう。そこで考えないといけないのが、スピンのx方向成分・y方向成分を表す行列です。量子力学が教えるところによると、このxyzそれぞれの方向を表す行列は、 \[X=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)\\Y=\left(\begin{array}{cc}0&-i\\i&0\end{array}\right)\\Z=\left(\begin{array}{cc}1&0\\0&-1\end{array}\right)\] となっています。(NOTゲートではなくてXゲートと呼ばれていたのはこういうわけなんです。) ちょっと量子力学の原理について説明した後、Xを例にとって量子力学が固有値と固有状態をどのように解釈しているのか説明していきたいと思います。
量子力学では、ある物理量に対して、それに対応する
物理量の行列
が必ずあります。(ここで何を言っているのかわからなくなる人が多いかもしれません。でも、これ以上に説明のしようが無いのです。とにかく、そういうものだと認めてもらわないと話が進みません。) そしてある物理量を観測したとき、観測される値は、必ずそれぞれの固有値のどれかになります。固有値以外の値が得られることがあってはいけません。また、観測しようとしている状態が、ある固有値の対応する固有ベクトルになっているときには、必ずその固有値が観測されます。一方で、そうなっていないときには、適当な確率でどちらかの固有値が観測されるのです。どういう確率かは後で例を挙げながら説明しましょう。
さて、ちょっと抽象的な説明が終わったので、x方向成分を表す行列 \[X=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)\] の固有値を考えてみましょう。固有値とは、 \[\left(\begin{array}{cc}0&1\\1&0\end{array}\right)\left(\begin{array}{c}\alpha\\\beta\end{array}\right)=\lambda\left(\begin{array}{c}\alpha\\\beta\end{array}\right)\] となるような\(\lambda\)のことでしたね。これを解くと、 \[\lambda = \pm 1\] となることがわかります。ついでに固有ベクトルも求めてしまうと、 \[\lambda = +1 \Rightarrow \frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\1\end{array}\right)\\ \lambda = -1 \Rightarrow \frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\-1\end{array}\right)\] となります。ベクトルの大きさが規格化してあるのは係数の絶対値の二乗が確率という意味を持つことを反映するためです。確率なのですから足したら1にしておかないといけませんね。
さて、z方向でも上向き(+1)と下向き(-1)の2つの状態\(\ket{0},\ket{1}\)があったように、x方向にも上向き(+1)と下向き(-1)があることがわかりました。そしてそれぞれの状態は、 \[\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\1\end{array}\right) = \frac{1}{\sqrt{2}} (\ket{0}+\ket{1}) = \ket{+}\\ \frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\-1\end{array}\right) = \frac{1}{\sqrt{2}} (\ket{0}-\ket{1}) = \ket{-} \] と表されます。x方向に\(\pm 1\)の固有値を持つ状態はそれぞれ\(\ket{+},\ket{-}\)と書かれることが多いです。さっき説明したことを適用すると、例えばあるqubitが\(\ket{+}\)の状態にあるとき、x方向成分を観測すると、必ず\(+1\)という結果が返ってくるという事になります。
さて、一方で、\(\ket{+}\)状態をz方向に観測するとどうなるでしょうか。最初に説明したことを思い出しましょう。 \[\alpha\ket{0}+\beta\ket{1}\] という状態を観測すると、\(\ket{0},\ket{1}\)がそれぞれ\(|\alpha|^2,|\beta|^2\)という確率で出るのでした。ということは、 \[\ket{+}=\frac{1}{\sqrt{2}} (\ket{0}+\ket{1})\] という状態を観測すると、1/2の確率で\(\ket{0},\ket{1}\)が観測されることになります。
さらに逆に考えて、\(\ket{0}\)をx方向に観測するとどうなるでしょうか。ちょっとむずかしいですが、次のように考えましょう。\(\ket{\pm}\)が\(\ket{0},\ket{1}\)で表せたのですから、逆に、 \[\ket{0}=\frac{1}{\sqrt{2}} (\ket{+}+\ket{-})\] のように、\(\ket{0}\)を\(\ket{+},\ket{-}\)によって表す事もできます。(このように別の表し方をすることを、x基底で
展開
する、と言ったりします。) つまり、\(\ket{0}\)というのは1つの状態であるわけでは無くて、実は\(\ket{+},\ket{-}\)が重ね合わさった状態だったというわけです。この\(\ket{+},\ket{-}\)の重ね合わせ状態を観測したときの振る舞いを考えてみます。x方向とz方向の観測について法則が違っていては困ってしまいますから、当然 \[\alpha\ket{+}+\beta\ket{-}\] という状態を観測したときは、\(\ket{+},\ket{-}\)がそれぞれ\(|\alpha|^2,|\beta|^2\)で出て来るべきでしょう。このように考えると、\(\ket{0}\)をx方向に観測したとき、\(\ket{\pm}\)がそれぞれ1/2の確率で観測される、と考えることができます。つまり、x方向の観測では、ある状態をx方向の固有状態\(\ket{+},\ket{-}\)で展開した時の係数が確率を決めて、その一方で、z方向の観測では、\(\ket{0},\ket{1}\)で展開した時の係数が確率を決めるという事になります。
さて、ここまで具体的な例でみてきたことを、もう少し一般的にまとめてみます。
- 量子力学では、私達が観測できる物理量それぞれに対応した行列があります。
- 物理量に対応した行列それぞれには、固有値\(\lambda_k\)・固有ベクトル\(\ket{k}\)があります。
- ある物理量を観測しようとした時、観測される値はその行列の固有値だけです。
- 量子力学的な状態\(\ket{\psi}\)は、物理量に対応する行列の固有ベクトル\(\ket{k}\)によっていつでも展開できます。つまり、\(\ket{\psi}=\sum_kc_k\ket{k}\)とできます。
- ある状態\(\ket{\psi}\)を観測したとき、ある固有値\(\lambda_a\)が観測される確率は、対応する固有ベクトル\(\ket{a}\)にくっついている係数\(c_a\)の大きさの二乗\(|c_a|^2\)になります。
5.観測
最後に、量子力学における「観測」の話をして終わりにします。さっきから、観測する確率は、、、とかなんとか言っていましたが、じゃあ観測した後はどうなるんだ、という話はしていませんでした。量子力学的な状態を観測すると、状態は観測結果で得られた状態に収縮します。
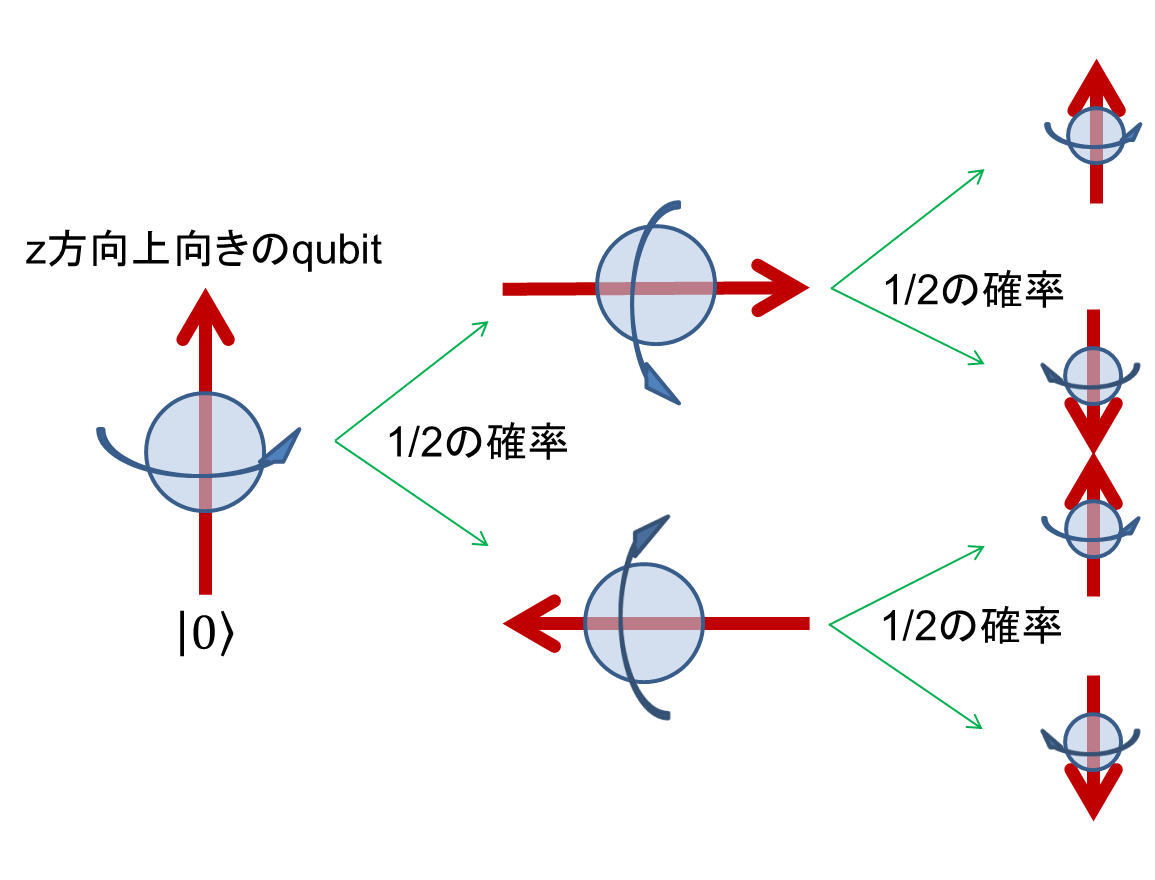
わけがわからないですね。具体的な例で見てみましょう。例えばさっきでてきた、\(\ket{+}\)状態をz方向に観測したとします。1/2の確率で\(\ket{0},\ket{1}\)のどちらかが「観測」されるのでしたね。観測結果が\(\ket{0}\)であったとしましょう。このとき、状態は\(\ket{0}\)に「収縮」します。式で表すとするなら、 \[\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\xrightarrow{\text{観測後}}\ket{0}\] このあと何回z方向に測定を行ったとしても (ノイズなんかで状態が変化しない限り)、状態は\(\ket{0}\)ですから\(\ket{0}\)という状態が100%の確率で観測されます。さて、これをx方向に測定するとどうなるでしょうか。\(\ket{0}\)をx方向に測定するわけですから1/2の確率で\(\ket{+},\ket{-}\)が測定されます。あれ? 最初\(\ket{+}\)に確定していた状態が、観測するだけでなぜだか\(\ket{-}\)にできてしまいました。なぜでしょう?
なぜこんなことになっているかは、実は誰もしらないのです。これをみんなが納得する形で説明できたらノーベル賞もの。最後に初回にも載せた図をおいておきます。