連続固有値をもつ波動関数とその直交性・規格化の方法
1.連続固有値の場合のハミルトニアン行列
シュレディンガー方程式 \[\hat{H}\left(x,-i\hbar\frac{d}{dx}\right)\psi(x) = E\psi(x)\tag{1}\] の固有値\(E\)はときに離散的になり、ときに連続的になる。離散的になる場合については、波動関数の直交性のページで書いたように、それぞれの波動関数が直交していることが示せた。ではなぜ波動関数が直交していることが重要だったのかというと、この波動関数を基底として扱うことによって、ハミルトニアン行列が勝手に対角化されるということがあったからだ。 では、ハミルトニアンが対角化されるということが、連続固有値の場合にどのように扱われるべきか考えてみよう。しかし対角化について考える前に、「ハミルトニアン行列に相当するもの」を連続固有値の場合にも考えてやらないといけない。
そこで離散固有値の場合を思い出すと、これまで話しているように、ハミルトニアンの行列要素は離散的な波動関数\(\psi_n\)を使って、 \[H_{mn}=\int\psi_m^*\hat{H}\psi_ndx\tag{2}\] のように計算できた。これは前回みたように対角行列になるのだった。
これにならって、連続固有値の場合にハミルトニアン行列に相当するものを定義しよう。連続固有値をもつ波動関数はそのエネルギー固有値によってラベル付けするのがいいだろうから、エネルギー固有値\(E\)をもつ波動関数を\(\psi_E(x)\)と書くことにする。このとき、 \[H(E,E')=\int\psi_E^*\hat{H}\psi_{E'}dx\tag{3}\] とすれば良さそうだ。さて、この(3)は対角行列的な性質を満たしているだろうか、ということが今回のテーマである。
が、そう簡単には話が進まない。実は連続固有値の場合には、(3)の積分が一般に収束してくれないのだ。そこで今回は簡単な例として、波動関数が連続したエネルギー固有値をもつ
自由粒子
を取り上げてから一般化していくことにする。2.自由粒子のシュレディンガー方程式とその解
自由粒子とは、外部から力を全く受けない粒子のことだ。したがって、その粒子が感じるポテンシャルエネルギー\(V(x)\)はいたるところ0である。つまり、1次元自由粒子のシュレディンガー方程式は \[-\frac{\hbar^2}{2m}\frac{d^2\phi(x)}{dx^2}=E\phi(x)\tag{4}\] となる。今回はこの方程式の解について考える。ともかく(1)を解いて一般解を見つけないと、お話が始まらないのでまずは解こう。(1)は次のように変形できる。 \[\frac{d^2\phi(x)}{dx^2}=-\frac{2mE}{\hbar^2}\phi(x)\] ここで\(k^2=2mE/\hbar^2\)とおいて、 \[\frac{d^2\phi(x)}{dx^2}=-k^2\phi(x)\] これはよくある単振動の方程式である。したがって一般解は \[\phi(x)=A\cos(kx)+B\sin(kx)\] または複素数で書くなら、 \[\phi(x)=Ce^{ikx}+De^{-ikx}\tag{5}\] だ。
ここで、量子井戸の問題のように、どこかで\(\phi(x)=0\)になるなんていう境界条件をつけると、それに応じて波数\(k\)が取りうる値が飛び飛びになる。しかし特に何も境界条件を指定しない場合、この\(k\)というのは連続的な値をとることができる。それにともなって、 \[E=\frac{\hbar^2k^2}{2m}\tag{6}\] で表されるエネルギー固有値\(E\)は連続的な値をとることができるのだ。ここでエネルギーが必ず正となることに注意しておこう。もし負のエネルギーを持つと、波数が虚数となり、波動関数が発散してしまうからだ。
3.自由粒子のハミルトニアン行列
(3)のように定義したハミルトニアン行列を計算してみよう。上の計算から、あるエネルギー固有値\(E\)をもつ波動関数\(\psi_E(x)\)は \[\psi_E(x)=A\exp\left(i\frac{\sqrt{2mE}}{\hbar}x\right)\tag{7}\] と書くことができる。よって、 \begin{align} H(E,E')&=\int_{-\infty}^\infty\psi_E^*\hat{H}\psi_{E'}dx \\ &=\int_{-\infty}^\infty\psi_E^*E'\psi_{E'}dx\\ &=E'|A|^2\int_{-\infty}^\infty\exp\left[\frac{i\sqrt{2m}}{\hbar}(\sqrt{E'}-\sqrt{E})x\right]dx \end{align} となる。この積分はまったくもって収束しない。被積分関数は単振動の波だから、無限遠で振動しているし、また、E=E'のときには積分は無限大に発散してしまう。4.ハミルトニアン行列が発散する問題の回避
ということで(3)の方法では自由粒子のハミルトニアン行列を計算することは不可能なのだ。しかし、これで不可能となると、位置の行列や運動量の行列を計算することも不可能だし、シュレディンガー方程式は連続固有値をもつ波動関数が出てきたときに、あまり使い物にならなくなってしまう。少し考えよう。このままでは積分が収束しなくて話が進まないので、とりあえず収束するような作り方がどんなものがあるだろうか。しかもなるべく(3)に近い作り方で、あわよくばある種の極限で(3)に成り代わる作り方がいい。
そこでこんなのはどうだろうか。エネルギー\(E\)のごく近くの波動関数を適当に重ね合わせて、
波束
を作り出し、それによってハミルトニアン行列を構成してみるのだ。(3)に戻りたいときにはエネルギーを重ね合わせる幅を0にする極限をとってみればいい。では例えば適当に和を取ってみて、 \[\phi_E(x)=\sum_{E_n}A_{E_n}\psi_{E_n}(x)\] としてみる。しかしこれだと、
そこで、 \[\phi_E(x,\epsilon)=\int_{E-\epsilon}^{E+\epsilon}\psi_{E'}(x)dE'\tag{7}\] という風に積分で重ね合わせてみよう。\(\epsilon\)というのは定数で、\(E\)の周りのどれだけの波動関数を重ねるか、ということを表すものだ。非常に小さくとれば、\(\phi_E(x,\epsilon)\)というのはほとんど\(\psi_E\)に等しくなる。
実際に(7)を計算してみると、 \begin{align} \phi_E(x,\epsilon)&=\int_{E-\epsilon}^{E+\epsilon}A\exp\left(i\frac{\sqrt{2mE}}{\hbar}x\right)dE' \\ &=A\int_{\sqrt{2m(E-\epsilon)}/\hbar}^{\sqrt{2m(E+\epsilon)}/\hbar}\exp\left(ik'x\right)\frac{\hbar^2k'}{m}dk'~~~(k'^2=\frac{2mE}{\hbar^2}とおいた)\\ &=A\frac{\hbar^2}{m}\int_{\sqrt{2m(E-\epsilon)}/\hbar}^{\sqrt{2m(E+\epsilon)}/\hbar}\exp\left(ik'x\right)k'dk' \end{align} この積分はwolframalphaに計算してもらうことにして、 \begin{align} &=A\frac{\hbar^2}{m}\left[\frac{k'e^{ik'x}}{ix}+\frac{e^{ik'x}}{x^2}\right]_{\sqrt{2m(E-\epsilon)}/\hbar}^{\sqrt{2m(E+\epsilon)}/\hbar}\\ &=A\frac{\hbar^2}{m}\left(\frac{k_+e^{ik_+x}-k_-e^{ik_-x}}{ix}+\frac{e^{ik_+x}-e^{ik_-x}}{x^2}\right)~~~(k_\pm=\sqrt{2m(E\pm\epsilon)}/\hbar)\tag{8} \end{align} 結構複雑な関数になってしまうが、グラフで書くと下のようになる。(絶対値をプロットした)
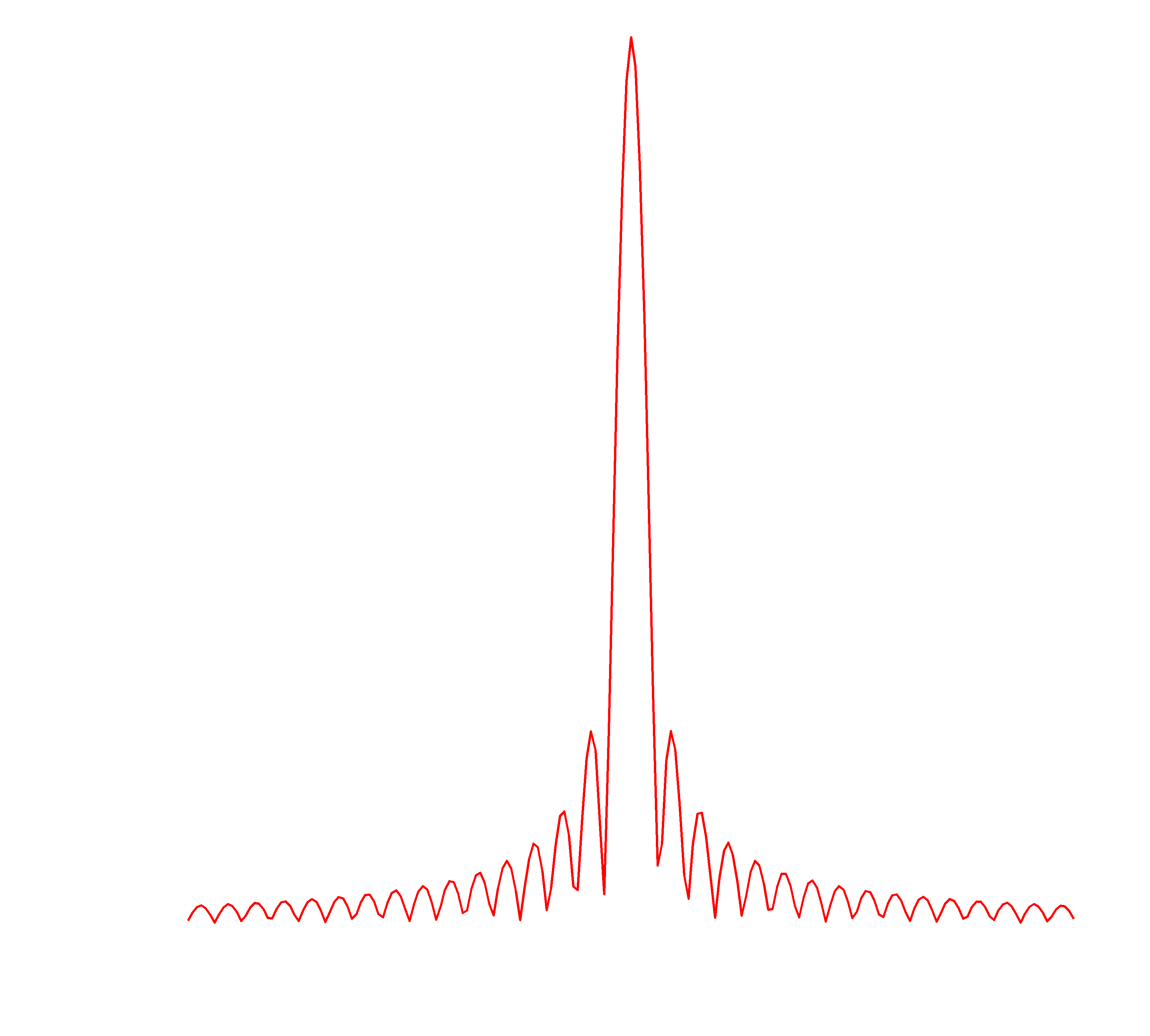
波束
を作り出すことができる。めんどくさいので重ね合わせた\(\phi_E(x,\epsilon)\)の積分\(\int_{-\infty}^\infty dx\)を実際に計算することはしないが、これは収束すると考えられる。なぜなら、よく知られているように\(\sin(x)/x\)の積分が収束するからだ。
と、いうことで、積分がうまいこと収束するように作り出した関数\(\phi_E(x,\epsilon)\)を使って、ハミルトニアン行列を定義するが、まあ(3)にならって、 \[H(E,E')=\int\psi_E^*\hat{H}\phi_{E'}(x,\epsilon)dx\] としよう。あ、でも忘れたらいけないのは、\(\epsilon\)というのは便宜上導入した定数だから、最後に極限をとって0にしないといけない。だから、 \[H(E,E')=\lim_{\epsilon\to 0}\int\psi_E^*\hat{H}\phi_{E'}(x,\epsilon)dx\tag{9}\] としてみる。しかし、これだと積分で定義されている\(\phi_E(x,\epsilon)\)が0になってしまって何も残らなくなるから、 \[\lim_{\epsilon\to 0}\frac{1}{\epsilon}\phi_E(x,\epsilon) = \psi_E(x)\] を使うことにして、 \[H(E,E')=\lim_{\epsilon\to 0}\int\psi_E^*\hat{H}\left(\frac{1}{\epsilon}\phi_{E'}(x,\epsilon)\right)dx\tag{10}\] のようにしてみよう。これならうまくいくだろうか?
5.連続固有値の場合の直交性
ということで、(9)や(10)のように作られるハミルトニアン行列が対角行列に相当する性質を持つかどうか調べよう。かなり雑に考えて、\(\epsilon\to 0\)の極限で、\(\hat{H}\)の作用している関数が\(\psi_E'\)になるのだから、\(\hat{H}\)は\(E'\)に置き換えても大丈夫だろう。そこで、 \[H(E,E')=E'\lim_{\epsilon\to 0}\int\psi_E^*\left(\frac{1}{\epsilon}\phi_{E'}(x,\epsilon)\right)dx\tag{11}\] となっていると考えよう。そして今から考えるのは、 \[\lim_{\epsilon\to 0}\frac{1}{\epsilon}\int\psi_E^*\phi_{E'}(x,\epsilon)dx\tag{12}\] のEの関数としての挙動だ。これがわかれば、Hの性質がわかるはずなのだ。前回やったのと同じようにやってみよう。まず、\(\phi_{E'}(x,\epsilon)\)は \[\phi_{E'}(x,\epsilon) = \int_{E'-\epsilon}^{E'+\epsilon}\psi_{E''}(x)dE''\tag{7再掲}\] だったから、この関数は \[\hat{H}\int_{E'-\epsilon}^{E'+\epsilon}\psi_{E''}^*(x)dE'' = \int_{E'-\epsilon}^{E+\epsilon}E''\psi_{E'}^*(x)dE'\] を満たす。そこで、\(\psi_E(x)\)のシュレディンガー方程式と並べて書いてみよう。 \begin{align} \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x)\right)\psi_E &= E\psi_E\\ \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x)\right)\int_{E'-\epsilon}^{E'+\epsilon}\psi_{E''}^*dE'' &= \int_{E'-\epsilon}^{E'+\epsilon}E''\psi_{E''}^*dE'' \end{align} この2つの式に他方の波動関数をかけて、引き算すると、 \begin{align} \psi_E\frac{d^2\phi_{E'}}{dx^2}-\phi_{E'}\frac{d^2\psi_E}{dx^2} &= \frac{2mE}{\hbar^2}\int_{E'-\epsilon}^{E'+\epsilon}(E-E'')\psi_E\psi_{E''}^*dE''\\ \end{align} で、xで積分する。 \[\int_{-\infty}^\infty\left(\psi_E\frac{d^2\phi_{E'}}{dx^2}-\phi_{E'}\frac{d^2\psi_E}{dx^2}\right)dx = \frac{2mE}{\hbar^2}\int_{-\infty}^\infty\int_{E'-\epsilon}^{E'+\epsilon}(E-E'')\psi_E\psi_{E''}^*dE''dx\]