演算子の正準交換関係と行列力学と波動力学の統合
1.ハイゼンベルク方程式とシュレディンガー方程式
電子は粒子である、という描像からスタートして、エネルギーの高い現象における古典論との対応原理から無理くり導き出されたハイゼンベルク方程式
は以下のような形をしていた。古典論でハミルトニアンが\(H(x,p)\)の形で書かれるとき、- \([X,P]=i\hbar I\)を満たす\(X,P\)を適当に持ってくる。(例えば調和振動子の行列)
- H(X,P)を計算して、それを対角化する行列\(U\)を求める。(このときに得られる固有値が定常状態のエネルギー)
- このときの\(X_0=U^*XU,P_0=U^*PU\)が求めたい位置と運動量になる。
ハイゼンベルク方程式
だ。でも、対応原理を押し進めて作られたこの方程式の\(\psi\)やX,Pという量には物理的な意味は与えられておらず、とりあえずこの方程式を解けば原子のスペクトルが正しく得られる、ということしか言えなかった。一方で電子は波である、という描像からスタートして、アインシュタインの提唱した光量子仮説をもとに類推しながら見つけられた
シュレディンガー方程式
は \[-\frac{\hbar^2}{2m}\frac{d^2 \phi}{dx^2} + V(x)\phi=E\phi\tag{2}\] という形をしていて、\(|\phi|^2\)には当初物質密度という意味付けがされていた。この方程式なら、電子の分布が直感的にわかる解が得られ、またエネルギー準位も(1)のハイゼンベルク方程式と全く同じ結果が得られるのだ。しかし、スペクトルの強度、というものを求めようとすると、やはりハイゼンベルクのほうに分があった。(2)では遷移の確率というのを見つけるのが不可能だからだ。でもだからといってほとんど(1)と同じ結果を得られ、しかも物理的な意味がわかりやすく、さらに解くのも簡単な(2)を捨てるのは惜しい。そこで今回は \begin{align} H(X,P)\psi &= W\psi\\ -\frac{\hbar^2}{2m}\frac{d^2 \phi}{dx^2} + V(x)\phi &= E\phi \end{align} という2つの式を一つにまとめあげることにする。
2.2つの式を見比べる
このままだとまだ関係性が見えてこないから、まずはハイゼンベルク方程式の方を一般的なハミルトニアンの形 \[H(X,P)=\frac{P^2}{2m}+V(X)\] を使って書き換えよう。すると、 \begin{align} \left(\frac{P^2}{2m}+V(X)\right)\psi &= W\psi\\ -\frac{\hbar^2}{2m}\frac{d^2 \phi}{dx^2} + V(x)\phi &= E\phi \end{align} というような2つの式の間の対応関係を暴いてやればいいことになるわけだ。さらに形を近づけて、 \[\left\{\begin{align} \left(\frac{P^2}{2m}+V(X)\right)\psi &= W\psi\\ \left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x)\right)\phi &= E\phi \end{align}\right.\tag{3} \] こうすると、対応関係が見え始める。 \[\left\{\begin{align} P^2&\Longleftrightarrow -\hbar^2\frac{d^2}{dx^2}\\ X&\Longleftrightarrow x\\ \psi&\Longleftrightarrow \phi\\ W&\Longleftrightarrow E \end{align}\right.\] となっているんじゃないだろうか。3.演算子の正準交換関係
上のような対応関係が成り立っているとするなら、シュレディンガー方程式で\(P,X\)にあたる演算子
も正準交換関係\([X,P]=i\hbar I\)を満たしているかチェックしておきたいところだ。でも、上の対応関係からPを決めようとしても、 \[P\Longleftrightarrow \pm i\hbar\frac{d}{dx}\tag{4}\] という感じで、符号が決まらないじゃないか。どっちがいいか決めるのに、2つともxとの交換関係を計算してみよう。
まず+の場合。
\begin{align} \left[x,i\hbar\frac{d}{dx}\right] &= x\cdot i\hbar\frac{d}{dx} - i\hbar\frac{d}{dx}\cdot x \end{align} ん?まあ最初の項は計算しようがないしほっといていいんだけど、二番目の項はどうしたらいいんだ?普通に微分して、 \[i\hbar\frac{d}{dx}\cdot x = i\hbar\] としていいのか?
いや、これじゃせっかく対応関係を見つけたと思ったのに、 \[\left[x,i\hbar\frac{d}{dx}\right] = x\cdot i\hbar\frac{d}{dx} - i\hbar\] となって全然だめじゃないか。ちょっと考えないといけないな。
4.演算子の掛け算・行列の掛け算
考えるのは、演算子の掛け算の方法なんだけど、今は行列と演算子の対応関係を考えているわけだから、それを考えるためにまず行列の掛け算を見直してみよう。行列の掛け算の計算方法は、少しでも線形代数をかじったことのある人ならだれでもしっているだろう。下の図のように計算されるのだった。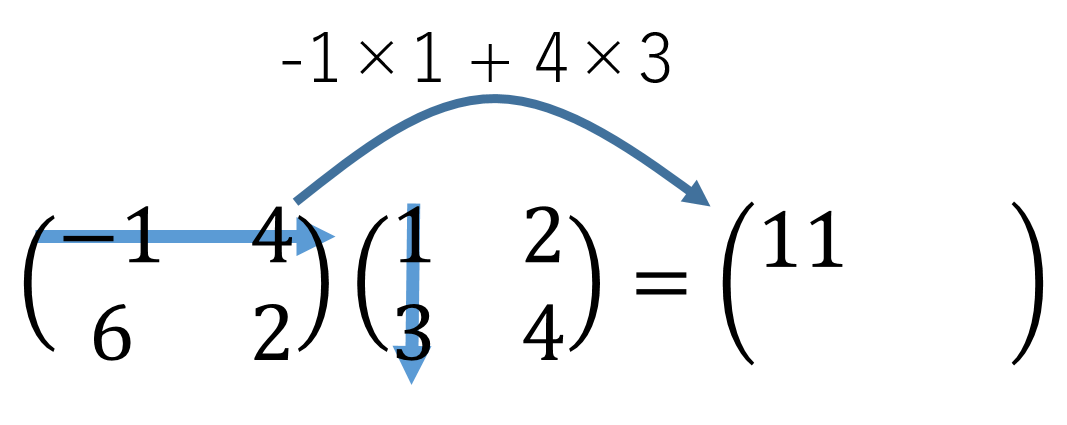
実はこの計算方法は、2つの線形写像の合成写像を、各々の行列表現の積によって表現できるようにしたい、というところから来ている計算方法なのだ。
脇道にそれるが、少し線形写像について。線形写像というのは、あるベクトル\(u\)を他のベクトル\(v\)に写すある種の操作で、その操作はある行列\(A\)に対して \[Au=v\] というような形で表すことができる。線形写像がこんな風に行列で表せる、ということは線形代数で非常に重要な意味を持っていた。この具体的な計算方法は下の図のように定義される。
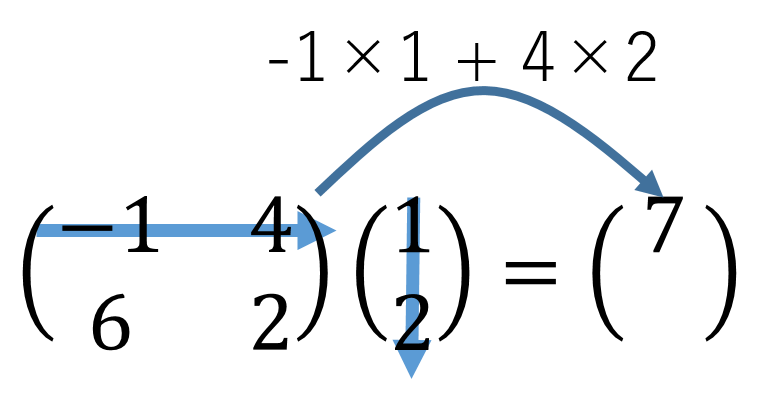
この図のように行列とベクトルの掛け算の方法を定義すると、行列と行列の掛け算は上のようにしないとよろしくない。上のように定義することによって、行列\(A\)と行列\(B\)があったとき、任意のベクトル\(u\)に対して\(A(Bu)= (AB)u\)が成り立つようにできるのだ。
任意のベクトル\(u\)に対して\(A(Bu)= (AB)u\)が成り立つように、行列の積が定義されている。これに習って、演算子の掛け算も定義してやろう。行列はベクトルを違うベクトルに写すものだから、任意のベクトルに対する性質で積を定義したが、演算子は関数にかかるものだから、任意の関数\(f(x)\)に対する性質で定義しないといけない。つまり、演算子\(\hat{A},\hat{B}\)の積\(\hat{A}\hat{B}\)とは、任意の関数\(f(x)\)に対して \[\hat{A}(\hat{B}f(x))=(\hat{A}\hat{B})f(x)\tag{5}\] を満たすものだ、と定義する。
5.再・演算子の正準交換関係
脇道が長くなってしまったが、ここからが本題だ。何をしていたのかというと \begin{align} \left[x,i\hbar\frac{d}{dx}\right] &= x\cdot i\hbar\frac{d}{dx} - i\hbar\frac{d}{dx}\cdot x \end{align} という交換関係を計算しようとしていたんだった。この式の二項目\(i\hbar\frac{d}{dx}\cdot x\)は、演算子の掛け算のやり方について考えて、(5)式のような定義の仕方にたどり着いたので、次のように考えないといけない。つまり、適当な関数\(f(x)\)をかけたときに、 \[i\hbar\frac{d}{dx}(xf(x)) = \hat{A}f(x)\] となるような演算子\(\hat{A}\)が\(i\hbar\frac{d}{dx}\cdot x\)の正体である。計算してみよう。 \begin{align} i\hbar\frac{d}{dx}(xf(x)) &= i\hbar f(x) + i\hbar x\frac{d}{dx}f(x) \\ &= \left(i\hbar + i\hbar x\frac{d}{dx}\right)f(x) \end{align} となるから、つまり、 \[i\hbar\frac{d}{dx}\cdot x=i\hbar + i\hbar x\frac{d}{dx}\tag{6}\] である。よって計算しようとしていた交換関係は \begin{align} \left[x,i\hbar\frac{d}{dx}\right] &= x\cdot i\hbar\frac{d}{dx} - i\hbar\frac{d}{dx}\cdot x\\ &=x\cdot i\hbar\frac{d}{dx} - \left(i\hbar + i\hbar x\frac{d}{dx}\right)\\ &=-i\hbar \end{align} となった。正準交換関係\([X,P]=i\hbar I\)と符号が違う。どうしたことか。でも、思い出してみれば、\(P\)という行列に対応している可能性のある演算子は\(\pm i\hbar\frac{d}{dx}\)という2つがあって、今はプラス側だけを計算したんだった。これでうまく行ってないということは、マイナス側が\(P\)という行列に対応しているということだろう。実際計算すると \[\left[x,-i\hbar\frac{d}{dx}\right] = i\hbar\tag{7}\] だからそういうことなのだ。これで、行列力学における\(P,X\)は波動力学において、 \[\left\{\begin{align} P&\Longleftrightarrow -i\hbar\frac{d}{dx}\\ X&\Longleftrightarrow x \end{align}\right.\] という対応がついていそうなことがわかった。次回からは、さらにこの対応関係を突き詰める。