シュレディンガー方程式による量子化とその解釈
1.量子井戸
学校でシュレディンガー方程式 \[-\frac{\hbar^2}{2m}\frac{\partial^2 \phi}{\partial x^2} + V(x)\phi=E\phi\tag{1}\] を習ったとき、十中八九最初に解かされるのが量子井戸の問題だろう。一番簡単に解ける問題だからな。いろんなところで解説されていると思うので、特にここで取り上げて解説はしないが、解は以下のようになる。 \[\phi_n(x)=A_n\sin\frac{n\pi x}{L}\tag{2}\] \[E_n = \frac{\hbar^2}{2m}\left(\frac{2\pi}{L}\right)^2n^2\tag{3}\] 図で表すと下のような感じだ。エネルギー準位と波の形を同時に示した。こういう図を見たときに勘違いしないでほしいのは、電子の波が本当に上に上がっていってるわけではないことだ。エネルギーが高い波を上に描いているだけで、一次元の波がこんなふうに空間的にちがうところにあるわけではない。
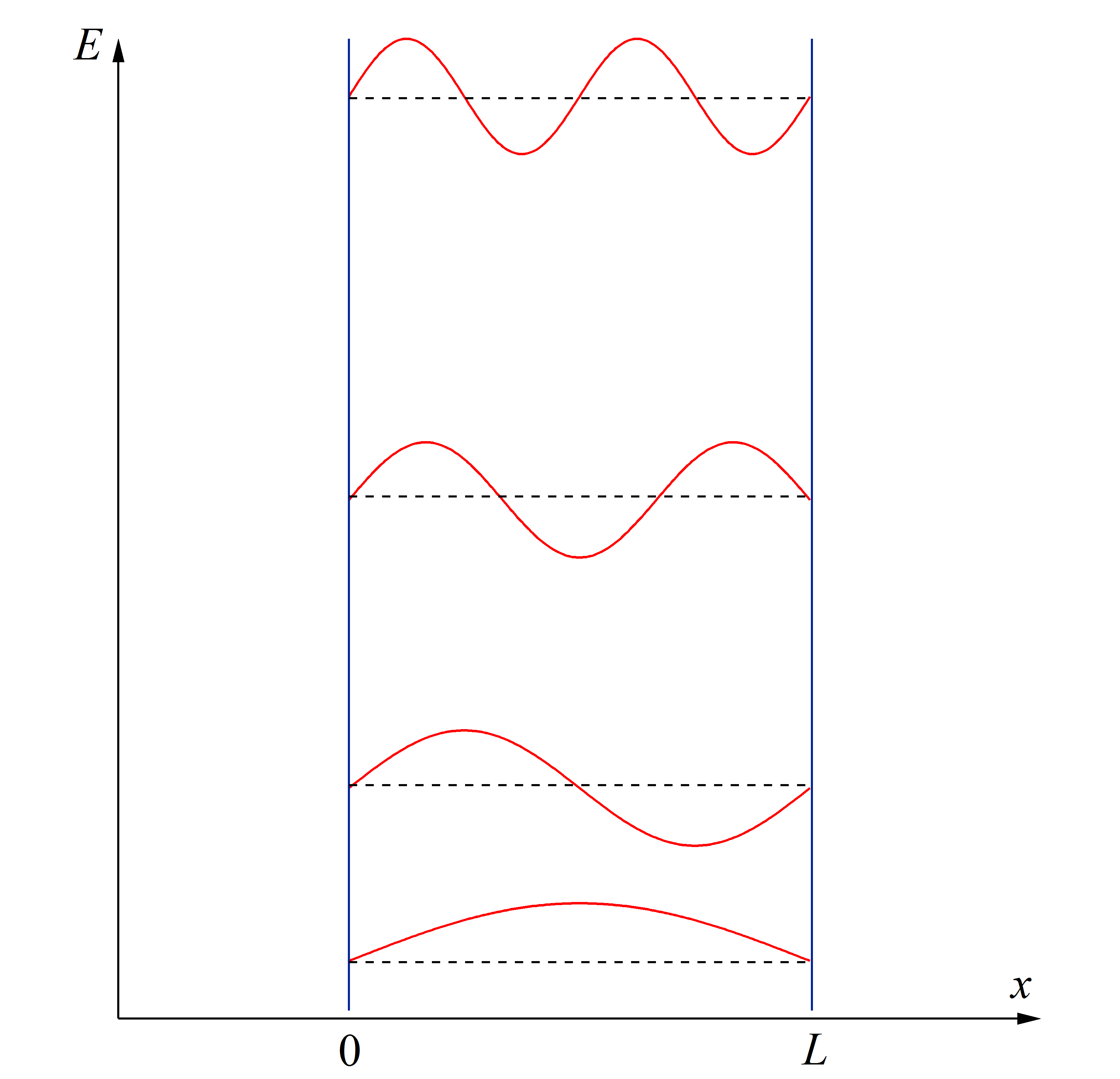
量子化
される原因になっていて、またこのことがシュレディンガー方程式の利点なのだ。といっても、これだけでは納得行かないと思うので色々と見てみよう。
2.調和振動子
そのうち微分方程式のほうで解説するが、調和振動子(\(V(x)=kx^2/2\))のシュレディンガー方程式 \[-\frac{\hbar^2}{2m}\frac{\partial^2 \phi}{\partial x^2} + \frac{k^2x^2}{2}\phi=E\phi\tag{4}\] に対する解は以下のようになる。 \[\phi_n(x) = A_n~H_n\left(\sqrt[4]\frac{mk}{\hbar^2}x\right)\exp\left(-\sqrt{\frac{mk}{2\hbar^2}}x^2\right)\tag{5}\] \[E_n = \hbar\sqrt{\frac{k}{m}}\left(n+\frac{1}{2}\right)\tag{6}\] ただし\(H_n(\xi)\)というのはエルミート多項式と呼ばれている関数で、 \[H_n(\xi) = (-1)^n e^{-\xi^2}\frac{d}{dx^2}e^{-\xi^2}\tag{7}\] である。上と同じように図を書いておこう。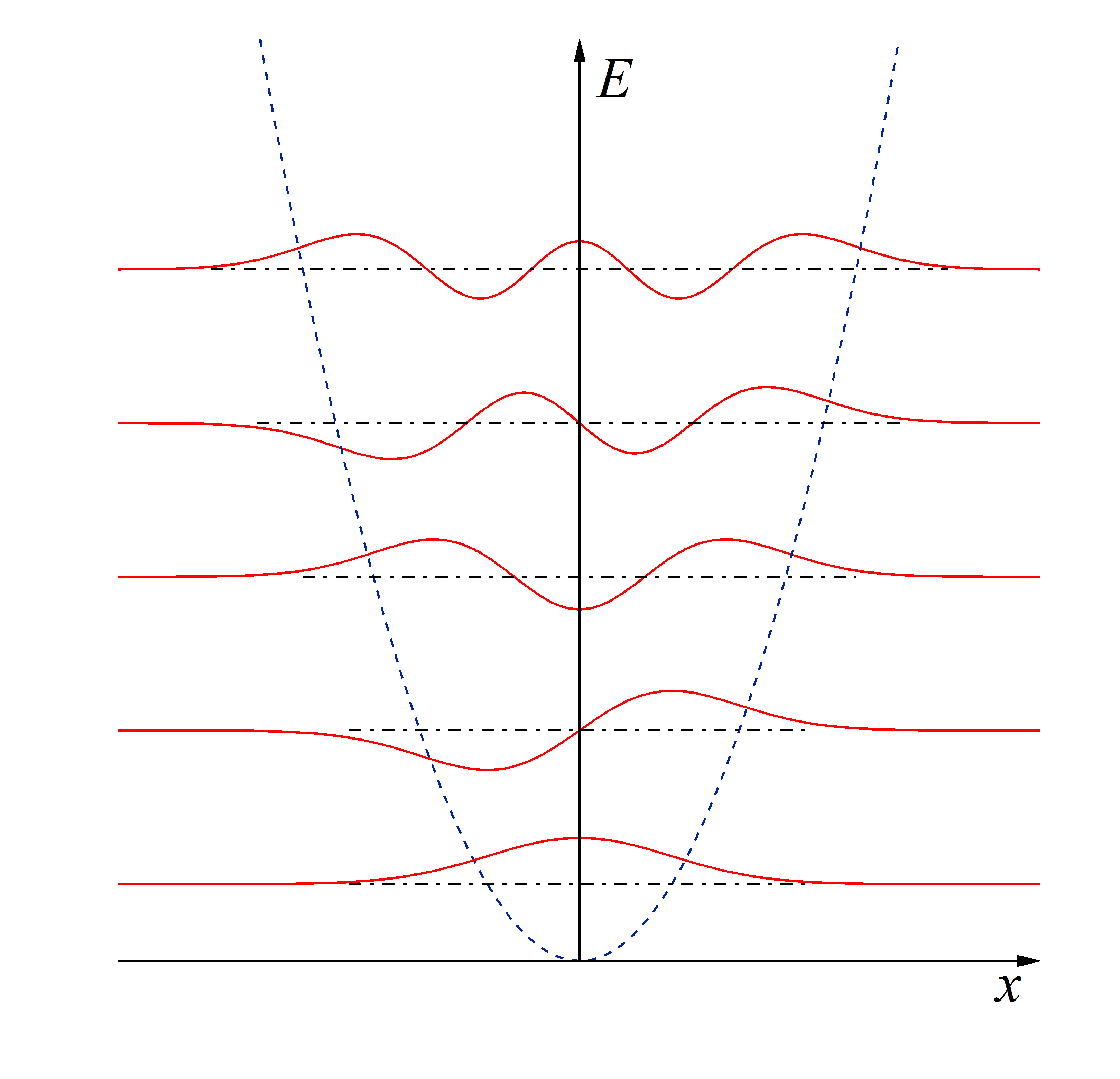
実はこの場合も境界条件が量子化を生み出している。(4)の微分方程式を解くのがすごくややこしいから途中でよくわからなくなってしまうが、調和振動子の解(5)というのは、波動関数が\(x\to\pm\infty\)のとき\(\phi(x)\to 0\)であるという無限遠での境界条件を使わないと得られない。(4)の微分方程式の解は無限遠で無限大に発散してもいいのなら、本当はもっとたくさんの解が可能なのだ。
ということで、量子化はこの調和振動子の場合にも、境界条件によって起こされるということがわかった。
3.水素原子
これもそのうち微分方程式のほうで解説するかもしれないが、水素原子\(V(\b{r})=-\frac{e^2}{4\pi\epsilon_0 r}\)のシュレディンガー方程式 \[-\frac{\hbar^2}{2m}\Delta\psi - \frac{e^2}{4\pi\epsilon_0 r}\phi=E\phi\tag{8}\] に対する解は以下のような形だった。 \[\psi_{nlm}(\b{r})=A_{n,l} r^l\exp\left(-\frac{r}{na_0}\right)L^{2l+1}_{n+l}\left(-\frac{2r}{na_0}\right)Y_{l,m}(\theta,\phi)\tag{9}\] \[E_{nlm}=-\frac{me^4}{32\pi^2\epsilon_0^2\hbar^2}\frac{1}{n^2}\tag{10}\] ただし、\(L(x)\)はラゲールの陪多項式、\(Y_{l,m}(\theta,\phi)\)は球面調和関数、\(a_0\)はボーア半径である。下にその様子を示しておこう。(a)が波動関数\(\psi\)、(b)がそれによる密度\(r^2|\psi|^2\)だ。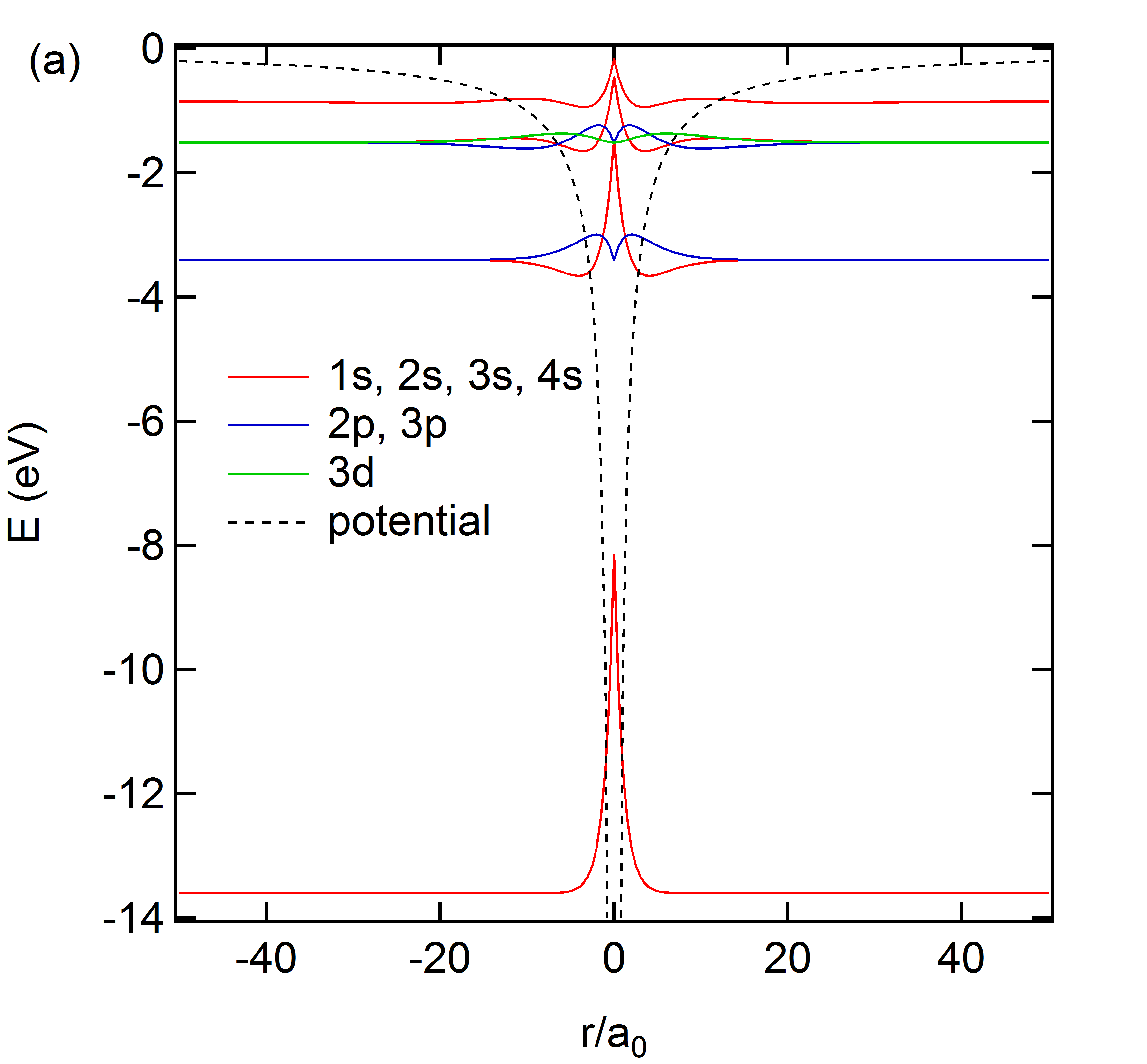
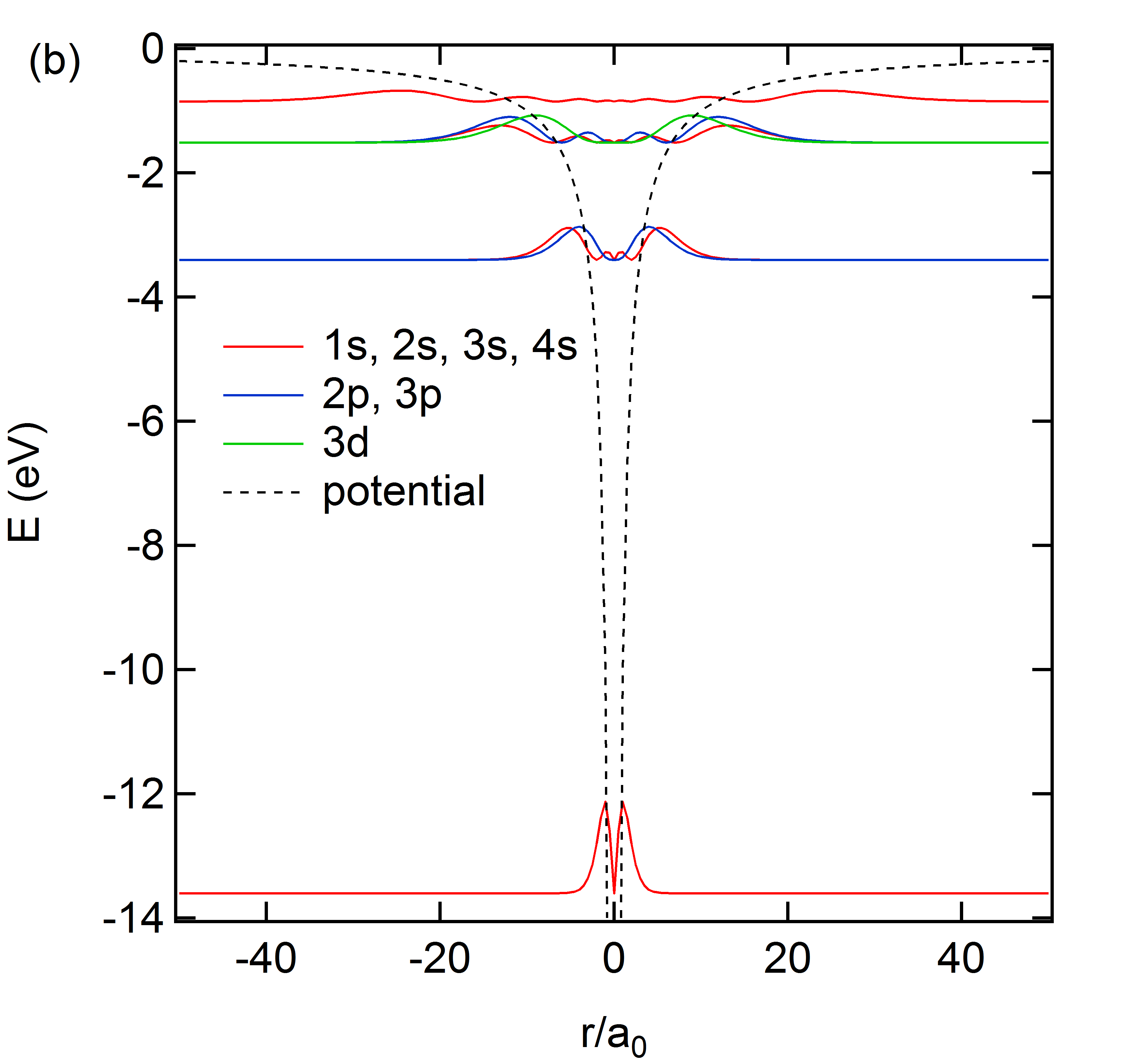
4.波動関数の解釈
ここまでを見ていると、電子の振る舞いは波のように解釈するのが理にかなっているように思える。この見方ならば、境界条件によって「自然に」量子化が起きるからだ。そうだとすると、電子が粒だという見方はそもそも全くの見当違いで、まったくもって間違っていたのだろうか。電子が粒子である、という立場にたって理論を立てると、粒子の角運動量は必ず\(\hbar\)の整数倍になっていなければいけないということを示す、 \[\oint p_idq_i = nh\tag{11}\] という量子条件を使わないと電子の振る舞いを説明することはできなかった。僕にはどうしたって、角運動量が飛び飛びの値をとるという条件よりも、物質波が無限遠で0にならないといけないという条件のほうが自然に思えてしまう。僕だけかもしれないが。
しかしやはり、電子がある種の粒であるという事実は、シュレディンガー方程式の\(\psi\)に対しても、必要とされるのである。例えば前回紹介したように、\(\psi\)が「物質波」であり\(|\psi|^2\)が物質密度を表すという解釈をするならば、その振幅に対して、 \[\int_V|\psi|^2 dV=m\tag{12}\] が必要となる。これは、物質波\(\psi\)の振幅がある決まった値しか取れないということを意味し、(12)というのはある種の量子条件になっていると考えることができるだろう。(12)というのは、光のエネルギーが\(h\nu\)の整数倍しか取り得ない、というのと同じくらい奇妙なことである。純粋に\(\psi\)が波だと考えるならば、普通はその振幅が連続的な値を取るべきなのだから。
現在の解釈にしても事情は同じだ。
現在では、\(|\psi|^2\)が物質密度を表すという解釈は全く見当違いだとされる。実験で電子を検出すると、電荷や質量というのは必ず電荷素量\(e\)や電子質量\(m\)が検出され、また、空間の一点で検出されてしまうからだ。もし、本当に空間的に\(|\psi|^2\)という密度で分布しているならば、何らかの実験で、質量が\(m/2\)となるような検出のされ方をされることもありうるはずだが、そういう実験は報告されたことがない。
そこで現在ではボルンが提唱したように、\(|\psi(x)|^2\)が位置xで電子を見つける確率密度であると考えられている、この解釈のもとでは、 \[\int_V|\psi|^2 dV=1\tag{13}\] という規格化を行うことになっているが、ここまでの議論をみればわかるように、この規格化条件自身が電子の粒子性を端的に表した物となっているわけだ。
なんとなく、大学の量子力学の授業ではシュレディンガー方程式を解いてエネルギー準位を求めることに終始しがちな気がしたので、こういう説明をしてみた。シュレディンガー方程式を解くだけでは、電子が波である、という印象しか得られない、というか僕はそういう感じだった。もしかしたら僕が工学部出身だからかも知れないが、せっかくの量子力学の授業ではこういう概念的な説明も色々してほしかったなあ、という気持ちを強く持っている。