量子位相推定アルゴリズム (Quantum Phase Estimation) とは
1. Quantum Phase Estimation
Quantum Phase Estimation
とは、ユニタリー行列の固有値を量子コンピューターによって計算するアルゴリズムです。タイトルでは日本語に直訳して「量子位相推定アルゴリズム」としましたが、日本語訳がこれで合ってるかどうかは定かではありません。多分まだなんと呼ぶのか定まって無いと思います。Kitaev が発表したので、Kitaev 位相推定なんて呼ばれ方もしているみたいです。さて、Phase Estimation がどんなことをするアルゴリズムなのか、まずは大雑把に解説します。
ユニタリー行列 \(U\) は、その固有値を必ず複素平面の単位円上にもち、\(e^{i\phi}\)の形で書くことができます。つまり、\(U\)の固有ベクトルの1つを\(\ket{\psi}\)として、 \[U\ket{\psi} = e^{i\phi}\ket{\psi}\] となります。この固有値\(e^{i\phi}\)の位相\(\phi\)を量子コンピューター上で近似的に求めるのが、Phase Estimationアルゴリズムです。
量子コンピュータ上で求める、ということの意味も簡単に説明しておきましょう。Phase Estimationでは、\(\phi\)を qubit の 1,0 によって2進数的に表現します。具体的には、\(\phi\)を\(2\pi\)で規格化して2進小数表記したもの、 \[\phi = 2\pi\times 0.\phi_1\phi_2\cdots\phi_n\] の各位の数字\(\phi_i = \{\text{0 or 1}\}\)をもつ状態\(\ket{\phi_1\phi_2\cdots\phi_n}\)生成することで、計算できたことにします。このqubitたちを測定してしまえば、ユニタリー行列の固有値が2進小数表記で求まるというわけです。当然\(\phi\)がちょうど使っているqubit数桁の2進小数で表せることは少ないですが、そのような場合には1番近い値を高い確率で出力します。
このくらいで大雑把な説明は終わって、次からは考え方を見ていきましょう。
2.Phase Estimationの考え方
まずはPhase Estimation に使う前提条件を書いておきます。- ユニタリー\(U\)は量子回路上に実装可能。
- さらに\(U\)はcontrolledに実行可能。(つまりcontroll qubitが1なら\(U\)を掛け、0なら掛けないということが可能。)
- 固有ベクトル\(\ket{\psi}\)を量子回路上に持っている。
ここからは便利のため、\(\ket{\psi}\)に対する\(U\)の固有値を\(e^{i2\pi \phi}\)と書きます。そうすると\(\phi\)は\(0\leq\phi\lt 1\)であるとみなせますね。さらにその2進小数表示を \[\phi = \sum_{k=0}^n 2^{-k}\phi_k = 0.\phi_0\phi_1\cdots\phi_n\tag{1}\] と書くことにします。最初は簡単のため、\(\phi\)が2進表記で有限桁であるとしましょう。
まず\(\ket{\psi}\)を持っているということで、それに\(U\)を掛ければ\(e^{i2\pi\phi}\)という位相を獲得した状態\(e^{i2\pi\phi}\ket{\psi}\)を作り出せることに注目します。こんなふうに状態の係数として現れた数字を、2進表記の状態ベクトル\(\ket{j}=\ket{j_0\cdots j_n}\)に埋め込む方法があればいいわけです。
そこで活躍するのが、前回紹介した
量子フーリエ変換
(Quantum Fourier Transform, QFT) です。QFTは、\(\ket{j}\)というqubitの状態を \[\ket{j} \xrightarrow{QFT} \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i\frac{2\pi kj}{2^n}\right)\ket{k}\tag{2}\] と変換するアルゴリズムでした。これの逆変換を考えると、実はこのアルゴリズムによって係数を状態に埋め込めることがわかります。QFT の逆変換、量子逆フーリエ変換 (Inverse QFT, I-QFT)は、(2)の状態を元に戻す変換です。 \[\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i\frac{2\pi kj}{2^n}\right)\ket{k}\xrightarrow{I-QFT} \ket{j}\tag{3}\] I-QFT 前では係数にあった\(j\)という数字が、変換後は\(\ket{j}\)と2進表記の状態ベクトルに埋め込まれています。確かにこれをうまいこと活用すれば、\(e^{i2\pi \phi}\)という係数を\(\ket{\phi}\)と状態ベクトルにできそうですよね。使いやすいように(3)式を少し書き直してみます。\(j\)は\(n\) bitの2進数ですから、各bitの数字を\(j_l\)として、\(j/2^{n}\)の部分は、 \[\frac{j}{2^{n}} = 0.j_1j_2\cdots j_n\] のような小数であることがわかります。だからこの\(j/2^n\)の部分を\(\phi\)に変えて、 \[\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i2\pi k\phi\right)\ket{k}\tag{4}\] という状態を作れば、あとは I-QFT をかけて\(\ket{\phi}\)を得られます。
さて、この係数\(\exp\left(i2\pi k\phi\right)\)を作るのは簡単です。単に\(\ket{\psi}\)に対して\(k\)回\(U\)を掛ければ良いだけです。 \[U^k\ket{\psi} = e^{i2\pi k\phi}\] ですからね。
3. Phase Estimation アルゴリズム
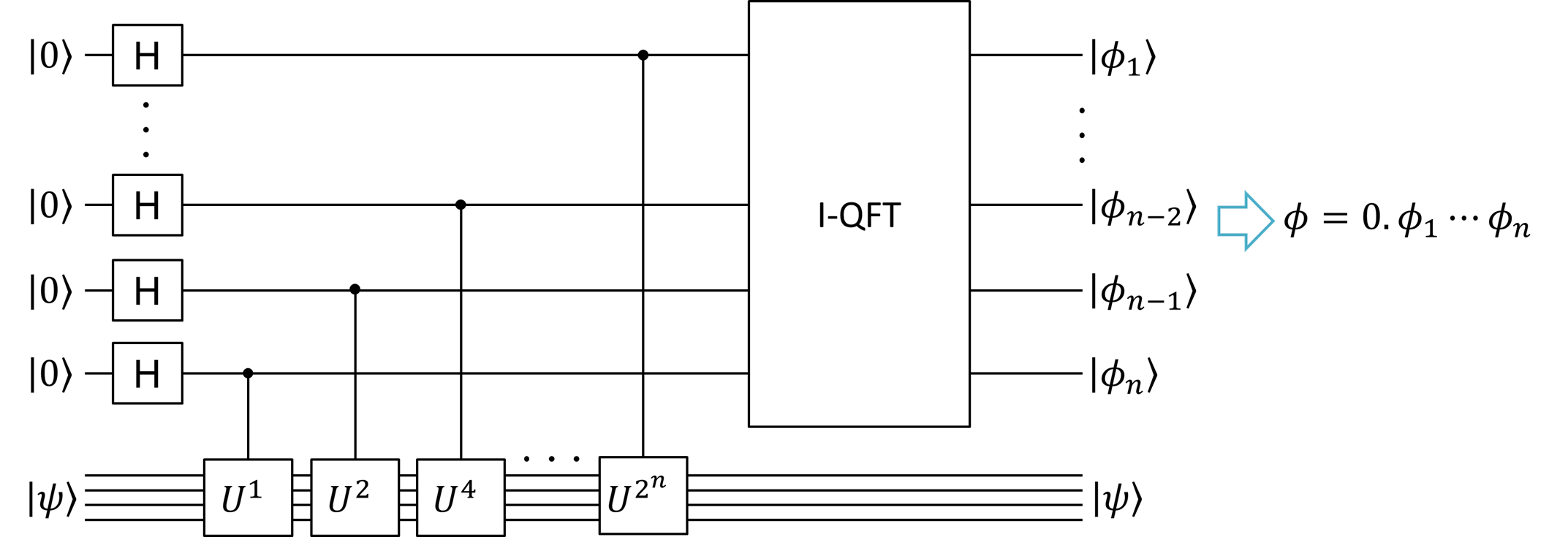
ここまでのことを踏まえて、Phase Estimation アルゴリズムを作ります。(4)式の形を踏まえて、まずは\(\ket{0}\)に初期化されていた\(n\) qubitのレジスターを \[\ket{0} \to \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k} \tag{5}\] と変換します。これはちょうど(4)式の係数部分だけが抜けた状態で、全ての\(\ket{k}\)が等しい重みで重ね合わされた状態です。この変換は簡単で、すべてのbitにアダマールゲート \[\ket{0}\xrightarrow{H}\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\] を掛ければ作り出すことができます。(アダマールゲートでなくても、この変換ができるゲートであればなんでも構いません。)
あとは\(\ket{k}\)に対応した係数\(\exp\left(i2\pi k\phi\right)\)を掛けましょう。これは、\(\ket{k}\)によってcontrollされた\(U^k\)を、別のqubit上にいる\(\ket{\psi}\)に掛ければ実現できます。\(\ket{\psi}\)も一緒に考えてPhase Estimation アルゴリズムの全貌は、 \begin{align} \ket{0}\ket{\psi} &\xrightarrow{H} \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\ket{\psi}\\ &\xrightarrow{c-U^k}\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i2\pi k\phi\right)\ket{k}\ket{\psi}\\ &\xrightarrow{I-QFT}\ket{\phi}\ket{\psi} \end{align} となります。量子回路も一緒に書いておきました。特にcontrolled-\(U^k\)の部分は、\(\ket{k}\)をbitに分解して\(\ket{k_{n-1}\cdots k_0}\) (\(k = \sum_l k_l2^l\)) と考えたとき、第\(l\) bit で controll した \(U^{2^l}\) を掛ければ、整数\(k\)ごとに\(U^k\)を掛けられることに注意しましょう。
4. \(\phi\)が\(n\)桁の2進小数で表せない場合
ここまでは簡単のために、\(\phi\)がちょうど2進小数で表せる場合を考えていましたが、\(n\)桁の2進小数で表せない場合にPhase Estimationがどのような状態を返すか見てみましょう。Phase Estimationによってせめて近似値が得られるかどうか、まずはざっくりと考えてみます。
最後にI-QFTを使っていますが、フーリエ変換・逆変換は本質的に区別が無いので、I-QFTであっても実際はフーリエ変換しているのと同じことです。離散フーリエ変換は与えられた離散信号の中から周期的な部分を見つけ出し、含まれている振動数に対応する番号に大きなピークを持たせるような変換でした。そこでフーリエ変換をかける直前、controlled-\(U^k\)が終わったところでの状態を見てみると、 \[\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i2\pi k\phi\right)\ket{k}\ket{\psi}\tag{6}\] となっています。その係数を \[a(k) = e^{i2\pi k\phi}\tag{7}\] と書くと、この\(a(k)\)は\(k\)に対して\(\phi\)という振動数を持って振動していることがわかります。だからこそ、フーリエ変換後には\(\phi\)に対応する\(\ket{\phi}\)の振幅だけが残ったわけです。このように考えると、フーリエ変換の性質から、\(\phi\)がちょうど\(n\)桁の2進小数になっていなくても、その近似値に当たる\(\ket{\tilde{\phi}}\)周辺の振幅が大きくなるはずです。
一応どのくらいの値が保証されているか数式で示しておきましょう。I-QFTは \[\ket{k} \xrightarrow{QFT} \frac{1}{\sqrt{2^n}}\sum_{m=0}^{2^n-1} \exp\left(-i\frac{2\pi km}{2^n}\right)\ket{m}\tag{8}\] という変換ですから、これを(6)に代入してゴリゴリ計算していきます。でもその前に、ちょっとした記号の準備をしておきます。
2進小数で1番\(\phi\)の真値に近い近似値を与えるbit列を\(\tilde{\phi}\)とし、誤差を\(\delta\)とします。つまり \[\phi = \tilde{\phi}2^{-n} + \delta\] です。\(\tilde{\phi}2^{-n}\)は\(n\)bitの2進小数ですから、誤差\(\delta\)の大きさは必ず\(|\delta|\leq 2^{-(n+1)}\)です。
準備はこれだけなので、あとは計算していきましょう。 \begin{align} &\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i2\pi k\phi\right)\ket{k}\\ &\xrightarrow{I-QFT} \frac{1}{2^n}\sum_{k=0}^{2^n-1}\sum_{m=0}^{2^n-1} \exp\left(i2\pi k\phi\right)\exp\left(-i\frac{2\pi km}{2^n}\right)\ket{m}\\ &=\frac{1}{2^n}\sum_{k=0}^{2^n-1}\sum_{m=0}^{2^n-1} \exp\left[i2\pi k\left(\delta+\frac{\tilde{\phi}-m}{2^n}\right)\right]\ket{m} \end{align} この状態において\(\ket{\tilde{\phi}}\)の振幅\(a_\tilde{\phi}\)を求めます。\(\ket{m}=\ket{\tilde{\phi}}\)の振幅部だけを取り出してやるには、\(m=\tilde{\phi}\)として\(m\)に関する和を無視すれば良いですね。 \begin{align} a_\tilde{\phi} &= \frac{1}{2^n}\sum_{k=0}^{2^n-1} \exp\left(i2\pi k\delta\right)\\ &= \frac{1}{2^n}\frac{\exp\left(i2\pi 2^n\delta\right)-1}{\exp\left(i2\pi\delta\right)-1}\\ &= \frac{1}{2^n}\frac{\exp\left(i\pi 2^n\delta\right)-\exp\left(-i\pi 2^n\delta\right)}{\exp\left(i\pi\delta\right)-\exp\left(i\pi\delta\right)}\frac{\exp\left(i\pi 2^n\delta\right)}{\exp\left(i\pi\delta\right)}\\ &= \frac{1}{2^n}\frac{\sin\left(\pi 2^n\delta\right)}{\sin\left(\pi\delta\right)}\exp\left(i\pi (2^n-1)\delta\right) \end{align} 次に\(\ket{\tilde{\phi}}\)を得る確率\(P(\tilde{\phi})\)を求めましょう。\(P(\tilde{\phi}) = |a_\tilde{\phi}|^2\)ですから、 \begin{align} P(\tilde{\phi}) &=\left|\frac{1}{2^n}\frac{\sin\left(\pi 2^n\delta\right)}{\sin\left(\pi\delta\right)}\exp\left(i\pi (2^n-1)\delta\right)\right|^2\\ &=\frac{1}{2^{2n}}\left|\frac{\sin\left(\pi 2^n\delta\right)}{\sin\left(\pi\delta\right)}\right|^2 \end{align} さて、これを下から評価して、最小値を求めます。よく知られているsinの性質、 \[|2x|\leq|\sin \pi x| \leq |\pi x| \quad\text{for}\quad x\in[-\pi,\pi]\] と、誤差の条件\(|\delta|\leq 2^{-(n+1)}\)を使います。そうすると、 \begin{align} P(\tilde{\phi}) &\geq\frac{1}{2^{2n}}\left|\frac{ 2\times 2^n\delta}{\pi \delta}\right|^2\\ &= \frac{4}{\pi^2} \sim 0.405 \end{align} が得られます。つまり、40%以上の以上の確率でPhase Estimationは正しい値を返すのです。意外と低いな、と思うかもしれませんが、先に言ったようにこの計算の本質はフーリエ変換ですから、正しい値の周辺の振幅もかなり大きくなっているはずです。つまり十分大きい\(n\)を使えば、Phase Estimationはほとんどの場合正しい値かその周辺の値を返すと考えられます。このあたりの話は、どこかにころがっている離散フーリエ変換の資料を読んだほうがわかりやすいでしょう。