Grover の検索アルゴリズム と Quantum Amplitude Amplification/Estimation
1. Groverのアルゴリズムと Amplitude Amplification
Grover の検索アルゴリズム
は、\(\frac{1}{\sqrt{N}}\sum_k\ket{k}\)という量子状態の中から、(1, 0) のみの値をとる条件関数\(f(x)\)が\(f(x)=1\)となるような量子状態\(\ket{x}\)を取り出すアルゴリズムです。このような問題は、古典的に行うと総当りをしなければならず\(O(N)\)の計算量となりますが、量子コンピューター上で行うと計算量が\(O(\sqrt{N})\)になることをGroverが発見しました。そのアルゴリズムは少し一般化され、現在では
Quantum Amplitude Amplification (量子振幅増幅)
という手法の一部とみなすほうがわかりやすくなっています。そこでこのページではまず Quantum Amplitude Amplification を説明し、その特別な場合として Grover アルゴリズムを解説します。Quantum Amplitude Amplification とは、適当な量子状態\(\ket{\psi}\)の中で、\(f(x)=1\)となるような量子状態の振幅だけを選択的に大きくし、観測時にそのような状態が得られる確率を高くする手法です。それでは解説していきます。
2. Amplitude Amplification
まず記号の定義と問題設定をしていきます。2進数\(x\)を引数として、1,0のどちらかを返す条件関数を\(f(x)\)とします。ある量子状態\(\psi\)のうち、\(f(x)=0\)を満たすような\(\ket{x}\)によって張られている部分を\(\ket{\psi_0}\)、\(f(x)=1\)を満たすような部分を\(\ket{\psi_1}\)と置きます。もう少し小難しく言うなら、\(\ket{\psi_{0,1}}\)はそれぞれ\(\{\ket{x}|f(x)=0,1\}\)という基底によって張られる超平面への\(\ket{\psi}\)の射影を規格化したものです。\(\ket{x}\)はもともと\(\braket{x}{x'}=\delta_{xx'}\)を満たしますから、当然\(\ket{\psi_0}\)と\(\ket{\psi_1}\)は任意の\(\psi\)について直交します。
式で書いておきましょう。 \[\ket{\psi} = \cos\theta\ket{\psi_0} + \sin\theta\ket{\psi_1}\tag{1}\] と置きます。そうすると、この状態を観測して\(f(x)=0\)となるような\(\ket{x}\)を見つける確率は\(\cos^2\theta\)であり、逆に\(f(x)=1\)となるような\(\ket{x}\)を見つける確率は\(\sin^2\theta\)です。\(f(x)=1\)となるような\(\ket{x}\)を見つける確率を上げるアルゴリズムをこれから検討します。なので\(\beta\)は最初比較的小さいものとしておきましょう。もし最初から大きいのであれば、普通にそのまま観測すればいいだけですからね。
3. 考え方
Amplitude Amplification アルゴリズムの発想は、以下の図でその全てを語ることができます。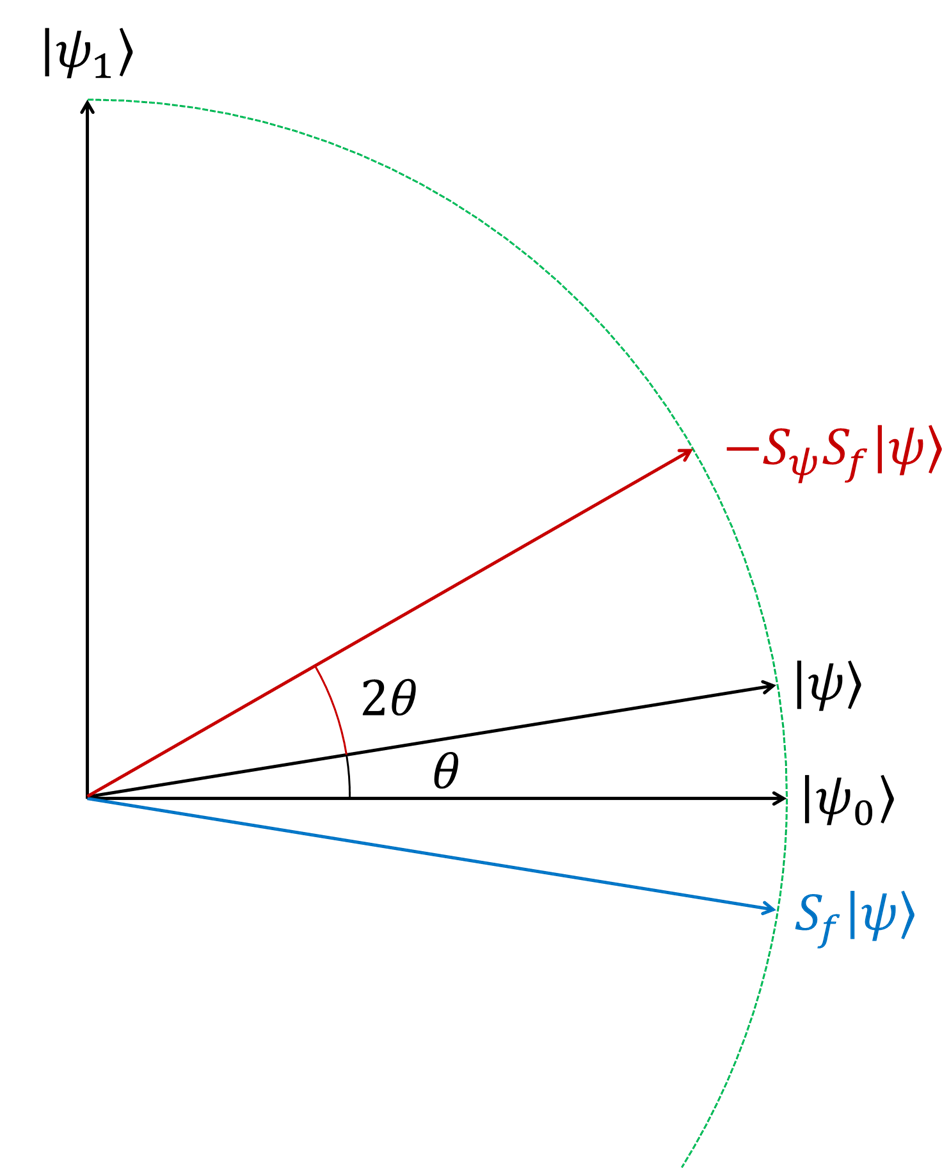
- \(\ket{\psi}\)を\(\ket{\psi_0}\)軸に関して反転する。(青) (\(=S_f \ket{\psi}\))
- さらに\(S_f \ket{\psi}\)を元のベクトル\(\ket{\psi}\)に関して反転する。(赤) (\(=-S_{\psi}S_f \ket{\psi}\))
このステップを繰り返せば、さらに\(\ket{\psi_1}\)に近づけられることもわかりますね。
4. \(S_f,S_\psi\)の具体的な形
Amplitude Amplificationの考え方はこれだけなのですが、このアルゴリズムが確かにうまく行くことを、ここからは計算によってしっかりと示しておきたいところです。さっきは実数の振幅だけを考えましたが、量子力学なので、本当は複素数の振幅も可能ですからね。そこでまずは反転変換\(S_f,S_\psi\)を具体的な作用で表してみます。\(S_\psi\)とマイナス符号をつけたのは、これも便利のためです。
\(S_f\)は\(\ket{\psi_0}\)に関する反転ですから、\(\ket{\psi_1}\)の符号を変えるような変換をすれば良いことがわかります。さらにいうなら、条件関数\(f(x)\)が1となるような\(\ket{x}\)についてのみ符号を変えるような変換です。つまり、 \[\begin{align} S_f \ket{x} &= \ket{x} & (\text{for}~ x ~\text{s.t.} ~f(x)=0)\\ S_f \ket{x} &= -\ket{x} & (\text{for}~ x ~\text{s.t.} ~f(x)=1) \end{align}\tag{2}\] です。これは以下の式と等価です。 \[\begin{align} S_f \ket{\psi_0} &= \ket{\psi_0} \\ S_f \ket{\psi_1} &= -\ket{\psi_1} \end{align}\tag{3}\] この式を使ってアルゴリズムの仕組みをみていきます。
もっと具体的に、\(f(x)\)から\(S_f\)を量子ゲートに分解して書き下したい、と思うかもしれませんが、Amplitude Amplificationではそこまでの具体性はもたせません。でもAmplitude Amplificationを本当に使うときには、自分が解きたい問題\(f(x)\)を、なんらかの方法で\(S_f\)という量子ゲートに書き下す必要があることは心に留めておきましょう。
次に\(\ket{\psi}\)に関する反転、\(-S_\psi\)を考えてみます。\(\ket{\psi}\)に関する反転とは、要するに、\(\ket{\psi}\)に直交する全ての基底\(\ket{\psi_\perp}\)について、符号を反転するような変換です。(3)式のような形で書いても良いのですが、良い書き方があるので少し天下り的ですが以下の式を使います。 \[-S_\psi = 2\ket{\psi}\bra{\psi}-I\tag{4}\] この\(S_\psi\)を\(\ket{\psi},\ket{\psi_\perp}\)に掛けてみれば、確かに\(\ket{\psi_\perp}\)だけの符号を反転していることが確認できます。ここで、(4)はもう少し簡単なゲートに分解できることを補足しておきます。\(\ket{\psi}\)は自分たちで作り出す状態ですから、これを初期化された\(\ket{0}\)から作り出すユニタリー\(U\)を私達は知っているはずです。だから(4)は以下のようにも書けます。 \begin{align} -S_\psi &= 2U\ket{0}\bra{0}U^\dagger-I\\ &= -U(I-2\ket{0}\bra{0})U^\dagger \\ &= -US_0U^\dagger \tag{5} \end{align} ここで\(S_0 = I-2\ket{0}\bra{0}\)としましたが、これは\(\ket{0}\)だけの符号を反転するようなユニタリーです。これならなんとかして実装できそうですよね。
5.計算
ここから計算していきます。便宜上、 \[\ket{\psi} = \alpha\ket{\psi_0} + \beta e^{i\phi}\ket{\psi_1}\tag{6}\] とします。\(\alpha=\cos\theta,\beta=\sin\theta\)は実数で、\(e^{i\phi}\)で振幅が複素数であることを入れています。やりたいことは、 \[Q = -S_\psi S_f\tag{7}\] という変換を\(\ket{\psi}\)に\(n\)回かけるとどうなるか示すことです。
まずは\(\ket{\psi}\)や\(Q\)を普通のベクトルと行列の表記に直します。基底を\(\ket{\psi_0},\ket{\psi_1}\)にとることに決めると、 \[\ket{\psi} = \left(\begin{array}{c}\alpha\\ \beta e^{i\phi}\end{array}\right)\tag{8}\] と表せることがわかると思います。\(\ket{\psi_0},\ket{\psi_1}\)は正規直交していますから、これで内積や行列の計算も簡単に行えるようになりますね。
行列\(S_f\)はどうなるでしょうか。\(S_f\)は\(\ket{\psi_1}\)成分だけを反転する変換でしたから、次のように書けます。 \[S_f = \left(\begin{array}{cc}1&0\\ 0& -1\end{array}\right)\tag{8}\] \(S_\psi\)は少しめんどくさいですが、(6)を代入して計算します。 \begin{align} S_\psi &= I - 2\ket{\psi}\bra{\psi}\\ &= I - 2\left(\alpha\ket{\psi_0} + \beta e^{i\phi}\ket{\psi_1}\right)\left(\alpha\bra{\psi_0} + \beta e^{-i\phi}\bra{\psi_1}\right)\\ &= I - 2\alpha^2\ket{\psi_0}\bra{\psi_0} + 2\beta^2\ket{\psi_1}\bra{\psi_1} + 2\alpha\beta e^{i\phi}\ket{\psi_1}\bra{\psi_0} + 2\alpha\beta e^{-i\phi}\ket{\psi_0}\bra{\psi_1} \end{align} となるので、基底を\(\ket{\psi_0},\ket{\psi_1}\)にとったときには、 \[-S_\psi = \left(\begin{array}{cc}2\alpha^2-1&-2\alpha\beta e^{-i\phi}\\ -2\alpha\beta e^{i\phi}& 2\beta^2-1\end{array}\right)\tag{9}\] と書けます。
ここまでやってしまえば、あとは単純な行列の演習問題で、 \begin{align} Q^n\ket{\psi} &= \left(\begin{array}{cc}2\alpha^2-1&-2\alpha\beta e^{-i\phi}\\ -2\alpha\beta e^{i\phi}& 2\beta^2-1\end{array}\right)^n\left(\begin{array}{cc}1&0\\ 0& -1\end{array}\right)^n\left(\begin{array}{c}\alpha\\ \beta e^{i\phi}\end{array}\right)\\ &= \left(\begin{array}{cc}2\alpha^2-1&-2\alpha\beta e^{-i\phi}\\ 2\alpha\beta e^{i\phi}& 1-2\beta^2\end{array}\right)^n\left(\begin{array}{c}\alpha\\ \beta e^{i\phi}\end{array}\right) \end{align} を頑張って計算するだけです。行列の\(n\)乗を計算するときには、固有値・固有ベクトルを求めるのが定石ですからまずはそれを計算します。
ここの計算過程は飛ばしますが、次のような固有ベクトル\(\ket{\psi_\pm}\)と対応する固有値\(\lambda_\pm\)が得られます。 \begin{align} \lambda_\pm &= \cos2\theta \pm i\sin2\theta = e^{\pm i2\theta}\\\\ \ket{\psi_\pm} &= \frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ \mp ie^{i\phi}\end{array}\right) = \frac{1}{\sqrt{2}}\left(\ket{\psi_0} \mp ie^{i\phi}\ket{\psi_1}\right) \end{align} この固有ベクトルによって元の\(\ket{\psi}\)を展開すると、 \[\ket{\psi} = \frac{1}{\sqrt{2}}\left(e^{i\theta}\ket{\psi_+} + e^{-i\theta}\ket{\psi_-}\right)\tag{10}\] となります。よって、これに\(Q^n\)を掛けた結果は、 \[Q^n \ket{\psi} = \frac{1}{\sqrt{2}}\left(e^{i(2n+1)\theta}\ket{\psi_+} + e^{-i(2n+1)\theta}\ket{\psi_-}\right)\tag{11}\] ですね。あとはこれを元の\(\ket{\psi_0,1}\)に戻してあげれば、 \[Q^n \ket{\psi} = \cos(2n+1)\theta\ket{\psi_0} + e^{i\phi}\sin(2n+1)\theta\ket{\psi_1}\tag{12}\] となっていて、たしかに複素数の振幅についても、さっきの図と同じようなことが起きることがわかりました。
6. Groverのアルゴリズム
(12)から、最初に\(\theta\)を知っていれば、適当な回数\(Q\)を繰り返すことによって\(\ket{\psi_1}\)を観測する確率を大きくできます。具体的には\((2n+1)\theta\)が\(\pi/2\)になるべく近づくような\(n\)を選べば良いわけです。これを踏まえて、Groverのアルゴリズムを見てみましょう。Grover が設定した問題は、\(n\) qubitの状態のうち、全ての\(\ket{0\cdots0}\cdots\ket{1\cdots1}\)を均等に重ね合わせた状態、 \[\ket{\psi_G} = \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \ket{k}\tag{13}\] から、ある\(\ket{j}\)を高い確率で取り出す方法はあるか?というものでした。ちなみにこの状態は、全てのqubitが0に初期化された状態\(\ket{0\cdots0}\)の各qubitに対して、Hadamard ゲート \[H\ket{0} = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\] を掛ければ作り出すことができます。
(13)の式の形を見ればわかるように、ある状態の\(\ket{j}\)の振幅\(\sin\theta = 1/\sqrt{2^n}\)は既知ですから、Amplitude Amplificationの手法をそのまま適用すれば簡単にその振幅を大きくすることができますね。
Grover のアルゴリズムはこれだけです。Amplitude Amplificationから見るととても簡単な問題でした。しかし、最初にこのような手法を提唱したので、\(Q\)は
Grover iteration
と言われることもあります。7. Amplitude Estimation
さて、最後にAmplitude Estimationについて紹介して終わりにしましょう。Amplitude Estimationは前回紹介したPhase Estimationの具体的な応用です。Grover iteration \(Q\)の固有値が\(e^{\pm i2\theta}\)であったことに注目すると、これにPhase Estimationを適用することで\(\theta\)を推定できます。Phase Estimation \(U_{PE}\)にはその推定情報を入れておくregister qubitも必要ですから、それも足しながら具体的に\(Q,\ket{\psi}\)を使って\(U_{PE}\)を使ってみると、 \[U_{PE}\ket{0}_{\text{reg}}\ket{\psi} \sim \frac{1}{\sqrt{2}}\left(\ket{\frac{\theta}{\pi}}\ket{\psi_+} + \ket{1 - \frac{\theta}{\pi}}\ket{\psi_-}\right)\] のような状態が得られます。(\(\theta/\pi\)が2進小数表記できない場合には近似的にこの状態になるので、\(=\)とせずに\(\sim\)としておきました。)
そうしてこの状態にいるregister qubitを観測すると \[x \approx \frac{\theta}{\pi}, ~1-\frac{\theta}{\pi}\] のどちらかの値が得られるわけです。これだとどちらを得たかわからないからだめじゃないか、と思われるかもしれません。しかしそもそも知りたいのは\(\sin\theta\)だったことをだったことを思い出すと、これでも良さそうです。なぜなら、得られた\(x\)に対して\(\sin(\pi x)\)を計算すれば、得られる値は \[\sin(\theta),~\sin(\pi-\theta) = \sin\theta\] となって、どちらも同じ値となるからです。
これでこの記事は終わりです。ここまで読んでくださる人がいるかどうかわかりませんが、おつきあいありがとうございました。