量子フーリエ変換 (Quantum Fourier Transform) とは
1.量子フーリエ変換とは
このページでは、量子コンピュータにおいて重要なアルゴリズムである、量子フーリエ変換 (Quantum Fourier Transform, QFT)
を解説します。量子フーリエ変換とは、信号処理の世界でよく知られている離散フーリエ変換を量子回路上に実装したものです。
このページでは離散フーリエ変換そのものの仕組みを説明することはしませんが、離散フーリエ変換とは、\(N\)個の離散データ\(\b{x} = \{x_j\}\)に対する次のような変換です。 \[y_k = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \exp\left(i\frac{2\pi kj}{N}\right)x_{j}\tag{1}\] (場合によって、指数関数の符号は変わるかもしれません。) もしくは、行列\(W_{kj}=\frac{1}{\sqrt{N}}e^{i2\pi kj/N}\)を定義すれば、 \[\b{y} = W\b{x}\tag{2}\] のように書くこともできます。この行列はユニタリ行列となっていることに注意しておきましょう。つまり、 \[W^\dagger W= W W^\dagger = I\] が成り立っています。量子回路では、測定を除くと基本的にユニタリ行列による変換しか許されていませんから、このフーリエ変換のユニタリ性というのはかなり大事です。
2.量子状態にデータを埋め込む
どんなアルゴリズム実行するにしても、データ\(\b{x}\)を量子状態として量子コンピュータに渡してあげなければ話が始まりません。そこでまず、どのように量子状態へと離散データ\(\b{x}\)を埋め込むかを紹介しましょう。量子コンピュータのアルゴリズム界隈では、ベクトル\(\b{x}\)を次のように埋め込むことが1番一般的です。 \[\ket{\b{x}} = \sum_{j=0}^{N-1} x_j\ket{j}\tag{3}\] ちょっと\(\ket{j}\)というのがわかりにくいと思うので、具体例で説明しましょう。例えば4次元のデータ\(x_0,x_1,x_2,x_3\)を埋め込むときは次のようにします。 \[\ket{\b{x}} = x_0\ket{00} + x_1\ket{01} + x_2\ket{10} + x_3\ket{11}\tag{4}\] つまり\(\ket{j}\)というのは、\(j\)という整数を2進表記した状態ベクトルを表すわけです。この方式によれば、\(n\) qubit に対して、\(2^n\)次元の情報を埋め込むことができます。
ただし、どのようにすればこんな状態が作り出せるか、ということは今回は考えません。これを作り出す効率的なアルゴリズムがあることを仮定して話を進めます。このように仮定されるアルゴリズムを総称して、オラクル(Oracle, 神託機械)と呼びます。計算機科学の言葉です。
(3)式のようなデータ形式を使うことにすると、あとは\(\ket{\b{x}}\)から \begin{align} \ket{\b{y}}&= \sum_{k=0}^{N-1} y_k\ket{k}\\ &= \sum_{k=0}^{N-1} \left[\frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} \exp\left(i\frac{2\pi kj}{N}\right)x_{j}\right]\ket{k}\tag{5} \end{align} を作り出すアルゴリズムを見つけられれば、量子コンピュータ上でフーリエ変換ができた! と言っても良さそうです。しかし結構複雑な式ですね。そこでもう少しだけ簡単な問題に置き換えましょう。(5)の和の順番を入れ替えます。 \[\ket{\b{y}} = \sum_{j=0}^{N-1} x_{j}\left[\frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} \exp\left(i\frac{2\pi kj}{N}\right)\ket{k}\right]\tag{6}\] この式をずっと見ていると、もともと\(\ket{\b{x}}\)は(3)のような式だったことを踏まえて、\(\ket{\b{x}}\)を(6)のようにするには、\(\ket{j}\)を \[\ket{j} \to \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1} \exp\left(i\frac{2\pi kj}{N}\right)\ket{k}\tag{7}\] と変換することと等価であることがわかります。そこでここからはこの(7)を作り出すことを目指して、説明していきます。3.QFTアルゴリズムの導出
ここからは本格的に導出です。難しいかもしれませんが、量子回路の計算に慣れるのにちょうどいい例題だと思うので、実際に手を動かしながらやってみるといいでしょう。まず、\(n\) qubitあるとき、使えるデータの次元は\(2^n\)ですから、これまで\(N\)と書いてきた次元を\(2^n\)と書くことにしましょう。つまりここからは \[\ket{j} \to \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i\frac{2\pi kj}{2^n}\right)\ket{k}\tag{8}\] を目指します。
実は、(8)式は積の形に分解できます。具体的には、 \[ \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i\frac{2\pi kj}{2^n}\right)\ket{k}\\\quad = \frac{1}{\sqrt{2^n}}(\ket{0}+e^{i2\pi 0.j_{0}}\ket{1})(\ket{0}+e^{i2\pi 0.j_{1}j_{0}}\ket{1})\cdots(\ket{0}+e^{i2\pi 0.j_{n-1}j_{n-2}\cdots j_0}\ket{1})\tag{9} \] となります。ただし、\(j_{n}\)は、整数\(j\)を2進表記した時の\(n\)桁目の数字 (1 or 0) で、\(0.j_{n-1}j_{n-2}\)のような表記は、その数字を並べた2進小数のことを表します。具体的に式で書くなら \[j=\sum_{l=0}^{n-1} j_l2^l\] \[0.j_{n-1}j_{n-2}\cdots j_{0} = j_{n-1}2^{-1} + j_{n-2}2^{-2} + \cdots + j_{0}2^{-n}\] です。
このこと ((9)式) を示しておきましょう。とは言っても、そこまで難しい計算ではありません。記号がたくさん出てきてわけが分からなくなっても、一つ一つ丁寧に考えていけばわかるはずです。 \begin{align} \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i\frac{2\pi kj}{2^n}\right)\ket{k} &= \frac{1}{\sqrt{2^n}}\sum_{k_0=0,1}\sum_{k_1=0,1}\cdots\sum_{k_{n-1}=0,1} \exp\left(i\frac{2\pi j}{2^n}\sum_{l=0}^{n-1} k_l2^l\right)\ket{k_{n-1}\cdots k_0}\\ &= \frac{1}{\sqrt{2^n}}\sum_{k_0=0,1}\sum_{k_1=0,1}\cdots\sum_{k_{n-1}=0,1} \prod_{l=0}^{n-1}\exp\left(i2\pi j k_l2^{l-n}\right)\ket{k_l}\\ &= \frac{1}{\sqrt{2^n}}\prod_{l=0}^{n-1}\left(\sum_{k_l=0,1}\exp\left(i2\pi j k_l2^{l-n}\right)\ket{k_l}\right)\\ &= \frac{1}{\sqrt{2^n}}\prod_{l=0}^{n-1}\left(\ket{0}+\exp\left(i2\pi j 2^{l-n}\right)\ket{1}\right)\\ &= \frac{1}{\sqrt{2^n}}\prod_{l=0}^{n-1}\left(\ket{0}+\exp\left(i2\pi 0.j_{n-1-l}\cdots j_0\right)\ket{1}\right)\\ &= \frac{1}{\sqrt{2^n}}(\ket{0}+e^{i2\pi 0.j_{0}}\ket{1})(\ket{0}+e^{i2\pi 0.j_{1}j_{0}}\ket{1})\cdots(\ket{0}+e^{i2\pi 0.j_{n-1}j_{n-2}\cdots j_0}\ket{1})\tag{9} \end{align} となり、示せますが、一応各等号の変形を説明しておきます。まず1番目の等式は、\(k\)の2進数表記を代入して、それに合わせて、\(\sum_k\)を各位の和\(\sum_{k_l=0,1}\)に書き換えました。2番目では指数関数の肩の和を積に置き換え、続いて3番目では各位の和記号を\(\sum_{k_0=0,1}\cdots\sum_{k_{n-1}=0,1} = \prod_l\sum_{k_l=0,1}\)とまとめてしまいました。その次4番目は問題ないとは思いますが、和を実行しただけです。次が、特に2進数の扱いに慣れていない人には少し難しいかもしれないので丁寧に説明します。 \[\exp\left(i2\pi j 2^{l-n}\right) = \exp\left(i2\pi 0.j_{n-1-l}\cdots j_0\right)\] を使ったわけですが、何をしたか説明するために、まず簡単な具体例を考えてみます。\(l=0\)とすると、\(j2^{-n} = 0.j_{n-1}\cdots j_0\)なのでこれは良いでしょう。\(l=1\)の場合はどうでしょうか? \[j2^{1-n} = 2\times 0.j_{n-1}\cdots j_0 = j_{n-1}.j_{n-2}\cdots j_0\] となりますね。このように順に考えてみると、一般の\(l\)の場合には \[j2^{l-n} = j_{n-1}\cdots j_{n-l}.j_{n-l-1}\cdots j_0\] です。これを指数関数にのせると、 \[\exp\left(i2\pi j 2^{l-n}\right) = \exp\left(i2\pi j_{n-1}\cdots j_{n-l}.j_{n-l-1}\cdots j_0\right)\] ですが、指数関数の\(e^{i2\pi n}=1\)という性質から、小数点より上の部分は無視しても良くなります。これによって、さっきの式が導かれるのです。
さて、\(\ket{j}\)に対する量子フーリエ変換の式を変形して、 \[ \ket{j} \xrightarrow{QFT} \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1} \exp\left(i\frac{2\pi kj}{2^n}\right)\ket{k}\\\quad = \frac{1}{\sqrt{2^n}}(\ket{0}+e^{i2\pi 0.j_{0}}\ket{1})(\ket{0}+e^{i2\pi 0.j_{1}j_{0}}\ket{1})\cdots(\ket{0}+e^{i2\pi 0.j_{n-1}j_{n-2}\cdots j_0}\ket{1})\tag{9} \] を導くことができました。あとはこれを量子回路に埋め込むだけです。
直接(9)を量子回路にしようとすると私は複雑すぎてわからないので、簡単な場合から考えてみましょう。
1 qubit の場合。
このときは \[\ket{j_0} \xrightarrow{QFT} \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi 0.j_{0}}\ket{1})\] なので、1,0の場合を個別に考えれば、下の図のように、単なるアダマールゲート、 \[H = \frac{1}{\sqrt{2}}\left(\begin{array}{cc}1&1\\1&-1\end{array}\right)\] をかけるだけで良いことがわかります。

そんなゲートを作れるのか?という疑問はごもっともですが、できるのです。一般に任意のゲートをあるqubitに対してcontrolledにするようなやり方が知られています。
そうすると、 \[\ket{j_1j_0} \to \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi 0.j_1j_0}\ket{1})\ket{j_0}\] とできて、最後にアダマールゲートを\(\ket{j_0}\)にかけてしまえば、 \[\ket{j_1j_0} \to \frac{1}{2}(\ket{0}+e^{i2\pi 0.j_1j_0}\ket{1})(\ket{0}+e^{i2\pi 0.j_0}\ket{1})\] が得られます。したがって、下の量子回路が 2 qubit QFTです。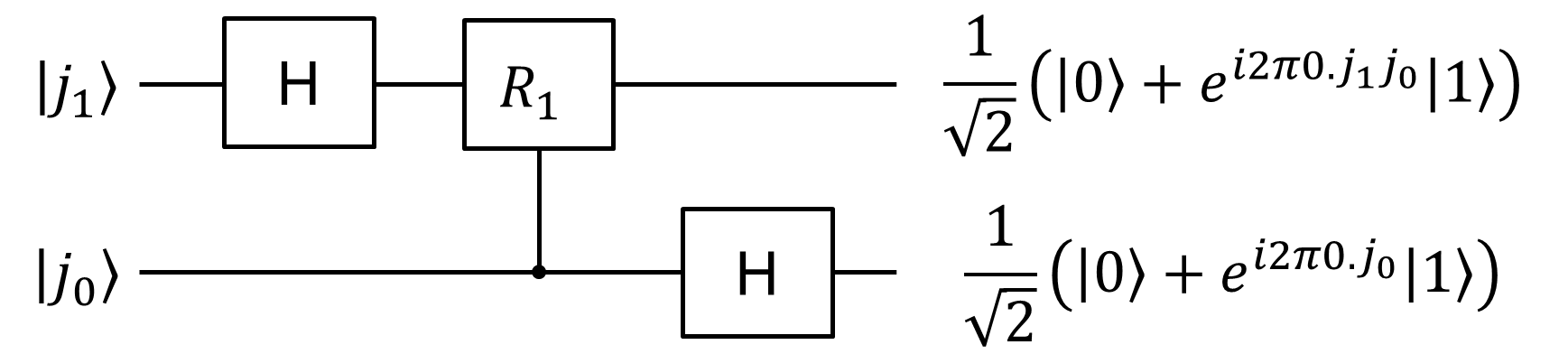
4. \(n\) qubit QFT の回路図
2 qubit までやってしまえば、あとはここまでの考え方をそのまま繰り返していくだけです。 \[R_k = \left(\begin{array}{cc}1&0\\0&e^{i2\pi/2^{k+1}}\end{array}\right)\tag{11}\] という位相ゲートを用意して、以下のような回路が量子フーリエ変換の全体像になります。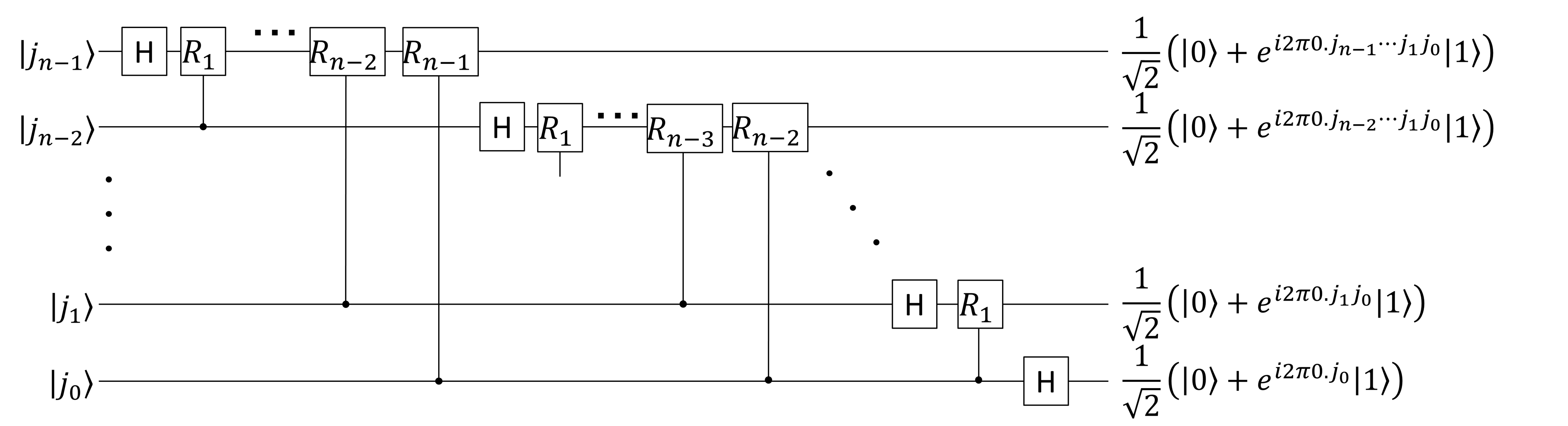
5. 高速性
一般的に離散データをフーリエ変換するときは高速フーリエ変換 (FFT) というアルゴリズムが使われます。FFTを使えば、サンプル数\(N\)に対して\(O(N\log N)\)の計算量で離散フーリエ変換が行えます。一方で QFT は、上の回路のゲート数を数えてみればわかるように、\(n\) qubitに対して\(n(n+1)/2\sim n^2\)で、\(O(n^2)\)の計算量です。
\(n\) qubitには\(2^n\)個のサンプルを埋め込めるのでしたから、QFTは\(N=2^n\)個のサンプルに対して、\(O(n^2)\)でフーリエ変換を行えることになります。比較のため\(N=2^n\)をFFTの計算量に代入して、FFTを同じ土俵に立たせてやると、 \begin{align} \text{FFT} &: O(n2^n)\\ \text{QFT} &: O(n^2) \end{align} となり、QFTのほうが圧倒的に早く実行可能であることがわかります。
これだけみると、おお、すごい!って感じです。しかし、量子状態の全ての係数を正確に取り出すには、指数関数的な時間がかかります。だから、単にFFTスペクトル全体を知りたい!というときには、普通に FFT を使って計算したほうが遥かにましです。でも、FFTのピーク位置だけ知りたい!というときには、QFTは有用です。なぜなら、周期的なデータに対してはその振動数に対応するある状態\(\ket{k}\)の振幅だけが大きくなり、少しの測定でピーク位置を得ることができるからです。実は、Shorの素因数分解や、Groverの検索アルゴリズムなどの有名なアルゴリズムは、このとこをうまく使っているのです。