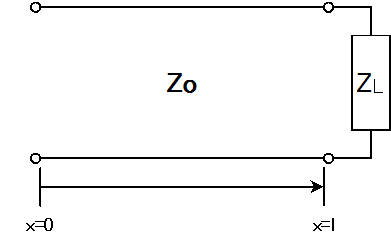1.反射
今回は特性インピーダンス\(Z_0\)、長さ\(l\)の線路を負荷\(Z_L\)で終端した時の解について考えてみましょう。送端からの距離をxとした時の電圧・電流の正弦波解は、次のように表されるのでした。
\[
\left\{
\begin{align}
V(x)&=K^+e^{-j\theta x} + K^-e^{j\theta x}\\
I(x)&=\frac{1}{Z_0}\left(K^+e^{-j\theta x} - K^-e^{j\theta x}\right)
\end{align}
\right.
\]
この場合、受端における境界条件\(V(l)=Z_LI(l)\)です。この式に上を代入します。すると、以下のように式を展開していくことができます。
\begin{align}
K^+e^{-j\theta l} + K^-e^{j\theta l}&=\frac{Z_L}{Z_0}\left(K^+e^{-j\theta l} - K^-e^{j\theta l}\right) \\\\
\left(\frac{Z_L}{Z_0}-1\right)K^+e^{-j\theta l}&=\left(\frac{Z_L}{Z_0}+1\right)K^-e^{j\theta l} \\\\
\frac{K^-e^{j\theta l}}{K^+e^{-j\theta l}} &= \frac{Z_L-Z_0}{Z_L+Z_0} \tag{1} \\\\
\end{align}
ここで\(K^-e^{j\theta l}\)と\(K^+e^{-j\theta l}\)というのはそれぞれ受端における電圧の反射成分と進行成分です。そこで、上の式を(受端における)
電圧反射係数
とよび、通常\(\gamma_v\)と表します。つまり、
\[\gamma_v=\frac{Z_L-Z_0}{Z_L+Z_0}\]
です。同様に電流反射係数\(\gamma_i\)も定義できます。電流の進行波成分は\(\frac{1}{Z_0}K^+e^{-j\theta x}\)、反射波成分は\(-\frac{1}{Z_0}K^-e^{j\theta x}\)ですから、(1)式にマイナスをかければ良いことがわかります。つまり、
\[\gamma_i=-\frac{Z_L-Z_0}{Z_L+Z_0}=-\gamma_v\]
です。
これらの式から言えることは、
特性インピーダンスと負荷インピーダンスが等しい時反射がおこらないということです。この条件を
インピーダンス整合
といいます。