電信方程式の導出
0.分布定数回路
分布定数回路とは、回路をもっと厳密に解こうとした時に出てきてしまうものです。普通の電気回路理論では、導線のインピーダンスなどというものは、完全に無視して理論が展開されていました。分布定数回路では、そのへんも考慮に入れて回路の電流・電圧を決めていきます。
長距離の電力伝送線路であったり、高周波の信号を扱うときにはこれが必須なのです。
何故ならば、ケーブルが長くなればそれだけそのインピーダンスは増えていくし、高周波になればそれだけキャパシタンス成分やインダクタンス成分が無視できなくなるからです。
1.電信方程式
今回は最初なので、分布定数回路の基礎となる電信方程式
の導出をしていきます。分布定数回路は、以下の図のような回路のことです。
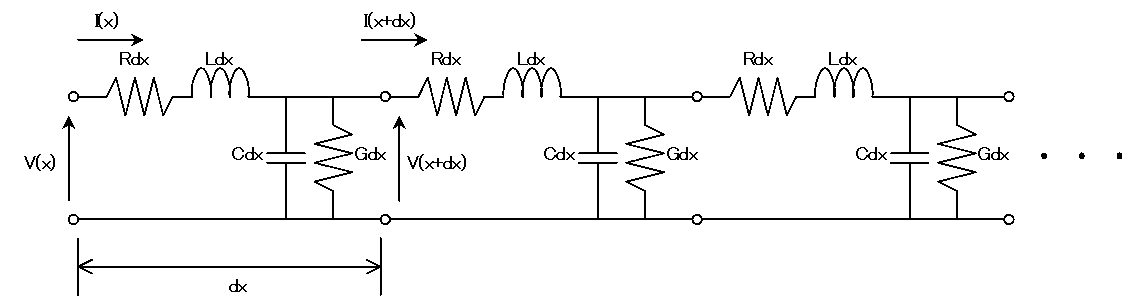
Rは単位長あたりの線路の抵抗
Lは単位長あたりのインダクタンス
Cは単位長あたりの線間容量
Gは単位長あたりの漏れコンダクタンス
を表します。特に、R,Gが0のものを
無損失線路
と呼びます。抵抗がなければ当然損失は0になるはずですからね。では、導出していきましょう。まずは電位や電流の関係を式にしてみます。図では時間変数tが抜けていますが適宜足して書いてます。 \[ \left\{ \begin{align} V(x,t)&=V(x+dx)+I(x,t)Rdx+\frac{\partial I}{\partial t}Ldx \\\\ I(x,t)&=I(x+dx)+V(x+dx,t)Gdx+\frac{\partial V}{\partial t}Cdx \end{align} \right. \] このような関係が成り立っていなければいけないことが、図からすぐにわかると思います。すでにかなり対称的ですね。さらに変形します。 \[ \left\{ \begin{align} \frac{V(x,t)-V(x+dx,t)}{dx}&=\left(R+L\frac{\partial }{\partial t}\right)I(x,t) \\\\ \frac{I(x,t)-I(x+dx)}{dx}&=\left(G+C\frac{\partial }{\partial t}\right)V(x+dx,t) \\\\ \end{align} \right. \] 左辺は明らかに微分の形になっていますから、微分の形に書き換えます。右辺の\(V(x+dx)\)はdxが非常に微小であると考えれば\(V(x+dx)=V(x)\)とできますね。
したがって、 \[ \left\{ \begin{align} \frac{\partial V}{\partial x}&=\left(R+L\frac{\partial }{\partial t}\right)I(x,t) \\\\ \frac{\partial I}{\partial x}&=\left(G+C\frac{\partial }{\partial t}\right)V(x,t) \\\\ \end{align} \right. \] を得ます。これが
電信方程式
です。導出もそんなに難しいことでは無いですから、すぐに導けるようになると良いです。次回からはこれを基本として議論を深めていきます。