理想気体の熱機関
理想気体による熱機関
ここからは少し今までの話の応用をしていこうかとおもう。まず
熱機関
とは、熱を力学的仕事に変化させる、そのシステムのことだ。車のエンジンなんかが分かりやすいだろう。 車のエンジンは、ガソリンを燃やすことで得られた熱を、車を動かすという力学的仕事に変えている。さっそくエンジンの動き を解析しよう、といいたいところではあるが、最初っからそれはちょっと難しいので少しずつ進んでいくことにする。定圧冷却→定積加熱→等温膨張
という理想気体を用いたサイクルを考える。p-V図を下においておく。なにを考えるかというと、 それぞれの変化において外界とどのくらいの仕事や熱のやりとりがあったか、ということについてだ。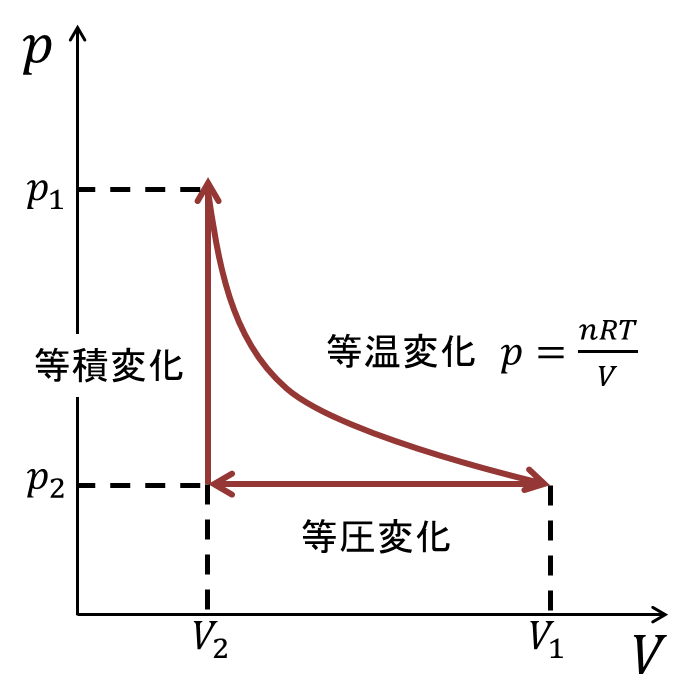
まずは定圧変化。
上のサイクルで定圧変化に当たるのは、図にも書いたが、下の矢印の部分である。体積が小さくなっているので、気体は 外界から仕事\(W_{in}\)をされている。どのくらいかというと、\(dW = -pdV\)であり\(V_1→V_2\)と変化しているので、
\begin{align} W_{in} &= -\int_{V_1}^{V_2} p_2 dV \\\\ &= -p_2\int_{V_1}^{V_2} dV \\\\ &= p_2(V_1 - V_2) \end{align} というふうに計算できる。つぎはこの変化の中で、どのくらいの熱量が流入したか考えよう。
また、気体の温度が定圧変化前\(T_h\)であったとすれば、定圧変化後の温度\(T_l\)は状態方程式から、
\[ \frac{T_h}{V_1} = \frac{T_l}{V_2} \] を満たす。ちなみに\(T_h\)というのは高い温度ですよーという意味でhighの頭文字を添え字にしてみた。\(T_l\)は分かるかもしれないが、 lowの頭文字をとって、低い温度ですよー、という意味合いだ。ともかく、上の式から、
\[ T_l = \frac{V_2}{V_1} T_h \] となり、等圧変化においては、前に扱った
定圧熱容量
\(C_p\)を用いて流出する熱量\(Q_{out}\)は次のように計算できる。 \begin{align} Q_{out} &= C_p (T_h - T_l) \\\\ &= C_pT_h \left(1-\frac{V_2}{V_1}\right) \\\\ &= C_p\frac{T_h}{V_1}(V_1 - V_2) \\\\ &= C_p\frac{p_2}{nR}(V_1 - V_2) \\\\ &... \end{align} こんな感じで色々変形できる。テストの問題とかであれば、特に指定がない限り当然どんな形の式を答えとして使っても よいわけだが、今回は\(W_{in}\)に使われている文字にあわせて変形した最後の行のやつを使うことにする。さて、 うえの議論をもとに、この変化で気体が得た正味のエネルギー\(\Delta U_p\)は、\[ \Delta U_p = W_{in} - Q_{out} = p_2(V_1 - V_2)(1-\frac{C_p}{nR}) \] となるが、前にみたように\(C_p\)は単原子気体で\( \frac{5}{3}nR \), 軸対称な分子の気体で\( \frac{7}{5}nR \)だったので \( (1-\frac{C_p}{nR}) \)は負である。だから
\[ \Delta U_p = -p_2(V_1 - V_2)(\frac{C_p}{nR}-1) \] のように表記したほうがわかりやすい。つまり、この変化において気体は内部エネルギーを減少させることが分かった。まあ とりあえずこの程度でよいだろう。
次に定積変化についてみていく。
が、定積変化では\(dV=0\)であるから、当然外界との仕事のやり取りはなく、\(dW=0\)である。したがってこの変化では、熱量の 出入りについて考えていく。定積で加熱したときの熱量の流入量は定積熱容量を用いて、
\[ Q_{in} = C_v (T_h - T_l) \] とかける。いちおう断っておくが、最後の変化が等温変化なので、高くなったときの温度はT_hだ。さっきの\(Q_{out}\)と同じように 変形をすることで次のようにまとめられる。
\[ Q_{in}=C_v\frac{p_2}{nR}(V_1 - V_2) \] こんなくらいしかここでやることはないだろう。
最後に等温変化。
等温膨張なので、この変化において気体は外界に対して仕事\(W_{out}\)をする。これは、積分によって
\begin{align} W_{out} &= \int_{V_2}^{V_1} p dV \\\\ &= \int_{V_2}^{V_1} \frac{nRT_h}{V} dV \\\\ &= {nRT_h}\int_{V_2}^{V_1} \frac{dV}{V} \\\\ &= nRT_h\ln\left(\frac{V_1}{V_2}\right) \\\\ &= p_2V_1\ln\left(\frac{V_1}{V_2}\right) \end{align} のように計算できる。ちなみに僕は\(\log_e\)よりも\(\ln\)を使うのが好きなのでそうする。
さらにこの変化で熱はどのくらい出入りしているかということについて考えたい。ここでよく考えてみると、気体の 内部エネルギーは温度にのみ依存するのだった。つまり、等温変化では内部エネルギーに変化がないわけだ。したがって このときに流入する熱量\(Q'_{in}\)は、外界に対してした仕事と同じであって、
\[ Q'_{in} = p_2V_1\ln\left(\frac{V_1}{V_2}\right) \] となる。
最後にこのサイクルの正味で入った熱量\(\Delta Q\)と正味で外にした仕事\(W\)を計算しておく。
\begin{align} \Delta Q &= Q'_{in} + Q_{in} - Q_{out} \\\\ &= p_2V_1\ln\left(\frac{V_1}{V_2}\right)+C_v\frac{p_2}{nR}(V_1 - V_2)-C_p\frac{p_2}{nR}(V_1 - V_2) \\\\ &= p_2V_1\ln\left(\frac{V_1}{V_2}\right)+(C_v - C_p)\frac{p_2}{nR}(V_1 - V_2) \\\\ &= p_2V_1\ln\left(\frac{V_1}{V_2}\right)-p_2(V_1 - V_2) \\\\ \\\\ W &= W_{out} - W_{in} \\\\ &= p_2V_1\ln\left(\frac{V_1}{V_2}\right)-p_2(V_1 - V_2) \\\\ \\\\ \Delta Q &= W \end{align} 変形の途中に\(C_p - C_v = nR\)の関係式を用いた。ともかくこれでエネルギー保存が成り立っていることが確認できた。 一応効率\(\eta\)も求められるが、書くのがめんどくさいのでちょっと書いて終わっておく。
\[ \eta = \frac{W}{Q'_{in} + Q_{in}}\] もう少し断熱変化とかもこのページに書くつもりだったが、長くなりすぎたので次回にまわすことにした。