統計力学の原理・エントロピーの定義と意味
1.平衡状態とは
統計力学をつくりだしたボルツマンは、その頃には量子力学が全く確立していなかったのにも関わらず、量子力学的な考え方で、統計力学を構築した。とくに、ある系がとる状態
というのが離散的になるということを考えだした功績が大きい。何しろ、原子というものが存在しているかどうかも怪しかった時代である。そんなことはさておき、統計力学は、考える系がある有限個の状態をとるとすることから始まる。状態の数というのは、例えば箱の中の気体分子のその一つ一つが、どの位置にいてどんな運動量を持っているか、その可能な組み合わせを全て足し合わせたものである。有限個とはいったものの、その組み合わせの数を全て考えるのは、ほとんど不可能で、その数は無限大に近い。
例えば、アボガドロ数\(10^{23}\)個程度の原子や分子が存在している普通の状態を考えてみよう。その分子や原子が2種類だけの状態をとる事ができるとしてもその組み合わせの数は実に \[2^{10^{23}}\approx 3\times10^{22}桁\] となる。\(10^{22}\)桁なんて、この時点でとてもじゃないが全ての組み合わせを考えるのは無理だ。いわゆる組み合わせ爆発というやつである。
しかし、確率で考えると、ほとんど0に近い組み合わせも存在するだろう。さっきの例を考えてみる。
N個の原子や分子が等確率で2種類の状態\(S_1, S_2\)をとるとき(粒子一つ一つは状態間の間を揺れ動いていて、ある適当な時間に観測してどちらかにいるということ)、\(S_1\)にn個、\(S_2\)にN-n個の粒子が存在する確率は、 \[p(n)=~_NC_n\left(\frac{1}{2}\right)^n \tag{1}\] となるだろう。簡単な二項分布である。よく知られているように、Nが大きい時(1)は次のように近似できる。(そのうち解説するつもり。) \[p(n)\approx \sqrt{\frac{2}{\pi N}}\exp\left[-\frac{2(n-\frac{N}{2})^2}{N}\right]\tag{2}\] わかることは、Nが大きい時、\(p(n)\)は\(n=N/2\)のまわりだけ大きな値を持って、それ以外の時ほとんど0であるということだ。ちなみにNが\(10^6\)のときのグラフを書いてみた。横軸がnである。
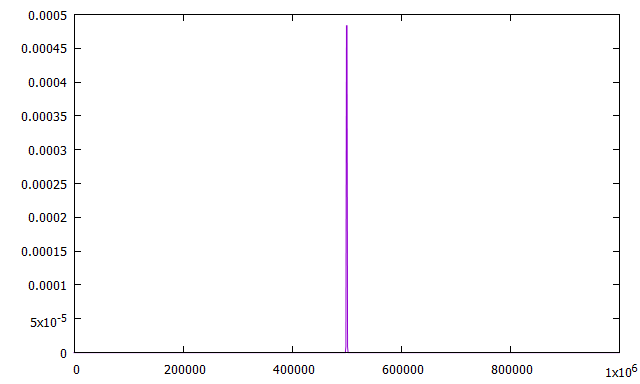
平衡状態
の考え方である。もし最初、何らかの方法でどちらかの状態に押しやったとしても、時間が経てば勝手に真ん中の状態に収束していってしまうだろう。そして、粒子一つ一つに注目すればそれぞれは状態の間を行き来しているが、平均的に全体で見れば\(S_1,S_2\)にほぼ半数ずつの粒子が存在する状況が作り出される。この、大きく見ればなにも変化の無い状態のことを平衡状態と定義するわけである。もちろん、片方だけに粒子が存在する可能性は、0ではない。しかし、その確率は、アボガドロ数個の粒子がいるなら、\(1/2^{10^{23}}\)だ。こんな低い確率の出来事はおきそうも無い。2.等重率の原理
さっきは、2つの状態を考えて、その状態を取る確率は等しく1/2とした。実は、統計力学では、このことを原理として認めてしまう。つまり、異なる状態は全て等確率で実現すると考えるのだ。このことを
等重率の原理
と呼んでいる。これは決して当たり前のことじゃない。確率の問題では、コイントスの表裏が1/2の確率で出ると仮定されたものも多いが、現実に本当に1/2になっているか?と考えてみれば、そんなことは無いだろう。コインのどちらかの面だけに重量が偏っていたら、軽い面のほうが少しだけ出やすい、なんていうこともあり得るはずだ。それと同じで、自然界の粒子が、どちらかの状態を取りやすい、なんていうことがありえるかも知れない。
だからこそ、
原理
としてしっかりと名前をつけて、統計力学ではこういうことを仮定していますよー、と明らかにしているわけだ。あくまでも仮定である。しかし、これを仮定することで、多くの実験結果が説明できてしまったから、統計力学は成功を収めているわけだ。3.温度とはなにか
さて、温度
を定義しよう。温度というのはとても身近な量であるわりに、良くわからないものだ。よく、分子運動の激しさが温度であるという言い方がされることもあるが、少なくとも僕にとっては、それでは理解出来たようなできてないような微妙な気分で終わってしまっていた。そこで、温度を次のように定義する。 (1). 「温度」とは、考えている系が平衡状態に達した時に、いたるところで等しくなる量である。
(2). 低い温度をもつ物質から、それよりも高い温度をもつ物質へ熱が自発的に流れることはない。
経験的にわかるだろう。熱いものと冷たいものをくっつけても、十分時間が経てば、その温度はほとんど等しくなる。もちろん、厳密な平衡状態、つまり完全にいたるところで温度が等しくなること、なんて現実に存在しないわけだが、変化のスピードが十分小さくなった時に、平衡状態とみなすことが多い。
普段直感的に温かい、冷たいなどと感じていることの基本的な性質を取り出したら、これだけで良かったのだ。
この定義は、温度計を作るのに非常に大切なものである。例えば、水が沸騰する温度を100℃、凍る温度を0℃と決めたとしよう。そのとき、沸騰している水と何かの物質、例えばよく温度計に使われる水銀なんかでいい、を接触させておくと、十分長い時間待つことでその物質は100℃に達すると考えられる。逆に氷水につけておけば、0℃ほどになる。これが言えるのは、(1)の定義があるからこそである。(最初の摂氏温度系は、そのときの水銀の体積変化を100分割することで作られた。当然、「温度」というものと水銀の体積変化が比例しているだろうという仮定があるわけだ。)
では、等重率の原理を使いながら、統計力学的に温度を定義してみよう。温度は、2つのものが平衡状態になったときに定義される量だから、まずは2つの系\(S_1, S_2\)を考えることが必要となる。2つの系はいろいろな状態をとることができるが、条件として持っているエネルギーを決めてやろう。そこで\(S_1,S_2\)はそれぞれエネルギー\(U_1, U_2\)を持っていると仮定する。このとき、2つの系は、与えられたエネルギーによって決まる状態数 \[g_1(U_1), g_2(U_2)\] を持っているだろう。この2つの系をエネルギーのやり取りだけができるようにつなげると、そのエネルギーは\(U=U_1+U_2\)となって、さらに、そのエネルギーに対応した状態の数 \[g(U)\] を持っていると考えられる。
さて、\(g(U)\)というのはつなげた系の取りうる状態全てを数え上げた数である。これを求めてみよう。2つの系をつなげた後にエネルギーが移動して、\(S_1\)がエネルギー\(u_1\)を持っているとすると、その時\(S_2\)は\(U-u_1\)のエネルギーを持っていることになる。それに対応して、\(S_1\)は\(g_1(u_1)\)、\(S_2\)は\(g_2(U-u_1)\)の状態数を持つはずだ。\(S_1,S_2\)へのエネルギーの分配は、合計のエネルギーが\(U\)になってさえいればいいから、全ての取りうる\(u_1\)について足し合わせれば、 \[g(U)=\sum_{u_1} g_1(u_1)g_2(U-u_1)\tag{1}\] と書けるだろう。
今温度を定義しようとしていたのだが、それには平衡状態の時にどういう量が等しくなっているかを考えればいい。そこで、状態数と言うのは、最初のグラフでも示したように、ある一つの場所にとても大きなピークをもつ関数だった。そして、平衡状態に達した時には、ほとんど確実に、そのピークの周辺にある状態をとるだろうということだった。
したがって、平衡状態の条件としては、 \[dg=0\tag{2}\] となっているべきである。つまり、gのピークを平衡状態として捉えるのだ。
一方(1)から、 \[dg=\sum_{u_1}\left[\left(\frac{\partial g_1(u_1)}{\partial u_1}\right)_{V_1,N_1}g_2(U-u_1)+g_1(u_1)\left(\frac{\partial g_2(U-u_1)}{\partial u_1}\right)_{V_2, N_2}\right]du_1\tag{3}\] (一応最初にエネルギーだけをやり取りできるようにしたと仮定したので、体積Vや粒子数Nを一定にしながら偏微分を行う必要がある。)これを0にするには、 \[\left(\frac{\partial g_1(u_1)}{\partial u_1}\right)_{V_1,N_1}g_2(U-u_1)+g_1(u_1)\left(\frac{\partial g_2(U-u_1)}{\partial u_1}\right)_{V_2, N_2}=0\tag{4}\] となっていれば十分だろう。\(u_2=U-u_1\)として二項目の微分を書き換えて整理すれば、 \[\frac{1}{g_1}\left(\frac{\partial g_1(u_1)}{\partial u_1}\right)_{V_1,N_1}=\frac{1}{g_2}\left(\frac{\partial g_2(u_2)}{\partial u_2}\right)_{V_2, N_2}\tag{5}\] となる。(5)式が、平衡状態において等しくなっているべき量だ。そこで、統計力学では、この量にある定数\(k\)をかけたものを次のように温度の定義とする。 \[\frac{1}{T}=k\frac{1}{g}\left(\frac{\partial g(u)}{\partial u}\right)_{V,N}\tag{6}\] なぜ逆数にするのかというのは、統計力学が始まる前からすでに知られていた熱力学の式、 \[\frac{1}{T}=\left(\frac{\partial S}{\partial U}\right)_{V,N}\tag{7}\] と見比べて決められたからだ。この式と比べながら、エントロピーも定義される。つまり、エントロピー\(S\)の統計力学の立場からの定義は、 \[S=k\log g\tag{8}\] である。こうすれば、(6)式を(7)式の形に書くことができて、あとは純粋に熱力学の議論が使える。(8)式が、エントロピーが系の乱雑さを示す指標であると言われるゆえんだ。
最後に、定数\(k\)を説明して終わることにしよう。\(k\)というのはよく知られているように、ボルツマン定数と呼ばれる量なわけだが、これまでの議論では、まったくもって\(k\)という定数を掛ける必然性が見えてこないだろう。実際、特にこの定数を掛けなくても議論をすすめることはできる。しかし、それまで知られていた理想気体の式なんかをそのまま使いたいと思った時に、この定数が重要な役割を果たして、うまいこと行くようになっているのだ。その辺りは、もう少し勉強を進めればわかってくると思う。