演算子の行列表現とその例
1.行列によるベクトルの変換
前回、関数を完全正規直交基底によってベクトル的に表現する方法について書いた。そこで今回は関数に作用する演算子についてそれを行列表示する方法について考えてみよう。そのために、まずは普通の行列をベクトルにかけて、ベクトルを変換するときの計算方法についておさらいする。行列とベクトルの掛け算というのは、下の図のように計算すればいいのだった。
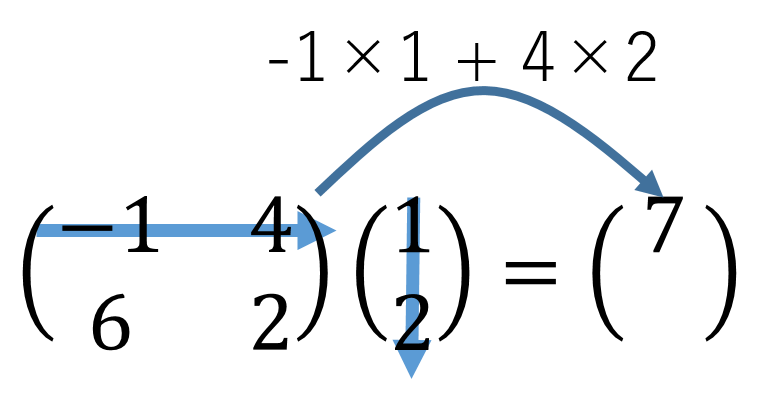
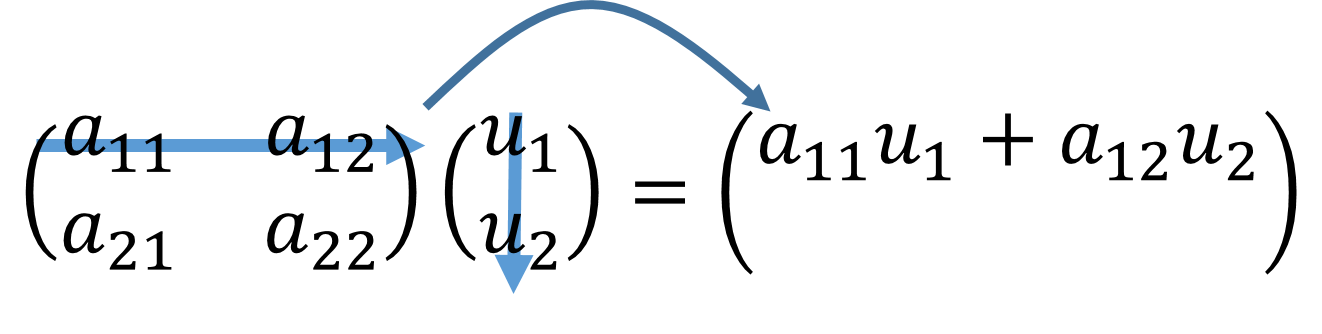
ここまでおさらいしたところで、演算子の行列表現について考えてみよう。
2.演算子の行列表現による関数の変換-微分演算子の例
まずは簡単な例からやってみよう。例えば微分演算子\(\hat{D}=\frac{d}{dx}\)を考える。関数としては、適当に今思いついた関数\(f(x)=a+bx+cx^2\)でも使おうか。多分このページを読んでいる人なら誰でもわかると思うが、この関数に\(\hat{D}\)をかけた関数\(g(x)=\hat{D}f(x)\)は\(g(x)=b+2cx\)だ。基底を\(1,x,x^2\)にとることにして、こいつらをベクトル表示してやろう。 \begin{align} f&=\left(\begin{array}{c}a\\b\\c\end{array}\right)\\ g&=\left(\begin{array}{c}b\\2c\\0\end{array}\right) \end{align} 微分演算子\(\hat{D}\)の行列表示を\(A_\hat{D}\)と書くことにすると、その行列は \[g=A_\hat{D}f\tag{2}\] を満たすはずだ。どういう行列が適当だろうか。
すぐにはわからないかもしれないが、基底ごとに考えてみると少しはわかりやすいと思う。例えば\(1\)に対して微分演算子\(\hat{D}\)をかけると\(0\)になる。つまり \[A_\hat{D}\left(\begin{array}{c}1\\0\\0\end{array}\right) = \left(\begin{array}{c}0\\0\\0\end{array}\right)\tag{3}\] が成り立つ。同じように\(x,x^2\)についても書き出してみると、 \[A_\hat{D}\left(\begin{array}{c}0\\1\\0\end{array}\right) = \left(\begin{array}{c}1\\0\\0\end{array}\right)\tag{4}\] \[A_\hat{D}\left(\begin{array}{c}0\\0\\1\end{array}\right) = \left(\begin{array}{c}0\\2\\0\end{array}\right)\tag{5}\] となる。(3)から(5)式を行列によってまとめると、 \[A_\hat{D}\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right) = \left(\begin{array}{ccc}0&1&0\\0&0&2\\0&0&0\end{array}\right)\tag{6}\] と書けるだろう。これはつまり、 \[A_\hat{D} = \left(\begin{array}{ccc}0&1&0\\0&0&2\\0&0&0\end{array}\right)\tag{7}\] であるということだ。これを\(f\)にかけてみると確かに\(g\)になることが確かめられる。
また、さらに次元を広げて、テイラー展開\(f(x)=\sum a_nx^n\)に対して基底を\(x^n\)にとったときの微分演算子は、 \[A_\hat{D} = \left(\begin{array}{ccccc}0&1&0&0&\cdots\\0&0&2&0&\cdots\\0&0&0&3&\cdots\\\vdots&\vdots&\vdots&\vdots&\ddots\end{array}\right)\] のように行列表示される。
このような例からもわかるように、関数をベクトル表示するときと全く同じように、演算子を行列表示するときには
基底
を選ぶことが非常に重要となる。3.一般論
上で具体的な例を見てみたから、ここからは一般論に入ろう。適当な正規直交基底\(\phi_n\)によって関数\(f\)が次のように展開されているとする。 \[f(x)=\sum_n f_n\phi_n(x)\tag{8}\] この関数に対して、適当な演算子\(\hat{O}\)をかける。 (適当な、とはいったが行列表示できる演算子は線形演算子だけだ。まあとりあえずはそういう種類のやつだけを考えることにしよう。) さらに、かけたあとの関数を\(g\)とする。 \[g(x)=\hat{O}f(x)\tag{9}\] 今からやることは、この演算子\(\hat{O}\)の行列表現\(A_\hat{O}\)をみつけること、つまり \[g=A_\hat{O}f=A_\hat{O}\left(\begin{array}{c}f_1\\f_2\\\vdots\end{array}\right)\tag{10}\] となる行列\(A_\hat{O}\)をみつけることだ。これも上でやったのと同じように、最初に基底について考えてみればいい。例えば\(\phi_1(x)\)に対して\(\hat{O}\)をかけた結果、 \[\psi_1(x)=\hat{O}\phi_1(x)\tag{11}\] のように\(\psi_1(x)\)に変換されたとする。\(\phi_1(x)\)というのは今正規直交基底として選んだ関数なんだから、 \[\phi_1=\left(\begin{array}{c}1\\0\\\vdots\end{array}\right)\tag{12}\] とできるはずだ。よって、 \[\psi_1=\left(\begin{array}{c}\psi_{11}\\\psi_{21}\\\psi_{31}\\\vdots\end{array}\right)\] となっているとして、(11)式をベクトル・行列表示してやると \[\left(\begin{array}{c}\psi_{11}\\\psi_{21}\\\psi_{31}\\\vdots\end{array}\right)=A_\hat{O}\left(\begin{array}{c}1\\0\\0\\\vdots\end{array}\right)\tag{13}\] となる。同じように、\(\psi_2(x)=\hat{O}\phi_2(x)\),\(\psi_3(x)=\hat{O}\phi_3(x)\)・・・などとやっていくと、 \begin{align} \left(\begin{array}{c}\psi_{12}\\\psi_{22}\\\psi_{32}\\\vdots\end{array}\right)&=A_\hat{O}\left(\begin{array}{c}0\\1\\0\\\vdots\end{array}\right)\\ \left(\begin{array}{c}\psi_{13}\\\psi_{23}\\\psi_{33}\\\vdots\end{array}\right)&=A_\hat{O}\left(\begin{array}{c}0\\0\\1\\\vdots\end{array}\right)\\ &\vdots \end{align} で、これらの式を行列でまとめて表してやると、さっきと全く同じように、\(A_\hat{O}\)を求めることができて、 \[A_\hat{O} = \left(\begin{array}{cccc}\psi_{11}&\psi_{12}&\psi_{13}&\cdots\\\psi_{21}&\psi_{22}&\psi_{23}&\cdots\\\psi_{31}&\psi_{32}&\psi_{33}&\cdots\\\vdots&\vdots&\vdots&\ddots\end{array}\right)\tag{14}\] が演算子\(\hat{O}\)の行列表示となる。
4.演算子から行列を作り出す。
(14)のように求められる演算子の行列表示だったが、具体的な計算のためにはそれぞれの成分、例えば\(\psi_{12}\)、とかがなんだったのか思い出さないといけない。これは、 \[\psi_1(x)=\hat{O}\phi_1(x)\] のように基底\(\phi_1\)を\(\hat{O}\)によって変換したときの関数\(\psi_1\)をベクトル表示 \[\psi_1=\left(\begin{array}{c}\psi_{11}\\\psi_{21}\\\psi_{31}\\\vdots\end{array}\right)\] したときの成分だった。ということは、例えば\(\psi_{21}\)を取り出す、というのは\(\psi_1\)の第二成分を取り出すことに相当するわけだ。こういうことをしたいときは、内積を使えばいい。 \[\phi_2\cdot\psi_1=\left(\begin{array}{c}0\\1\\0\\\vdots\end{array}\right)\cdot\left(\begin{array}{c}\psi_{11}\\\psi_{21}\\\psi_{31}\\\vdots\end{array}\right)=\psi_{21}\] とできるからだ。さらに\(\psi_1=\hat{O}\phi_1\)だったことを使うと、 \[\psi_{21}=\phi_2\cdot(\hat{O}\phi_1)\tag{15}\] であり、一般に\(\psi_{mn}\)は \[\psi_{mn}=\phi_m\cdot(\hat{O}\phi_n)\tag{16}\] となる。よって行列\(A_\hat{O}\)は \[A_\hat{O} = \left(\begin{array}{ccc}\phi_1\cdot\hat{O}\phi_1&\phi_1\cdot\hat{O}\phi_2&\cdots\\\phi_2\cdot\hat{O}\phi_1&\phi_2\cdot\hat{O}\phi_2&\cdots\\\vdots&\vdots&\ddots\end{array}\right)\tag{17}\] と計算される。関数同士の内積として、よく使われる \[f\cdot g=\int f^*(x)g(x)dx\tag{18}\] を採用するなら、 \[A_\hat{O} = \left(\begin{array}{ccc}\int\phi_1^*(x)\hat{O}\phi_1(x)dx&\int\phi_1^*(x)\hat{O}\phi_2(x)dx&\cdots\\\int\phi_2^*(x)\hat{O}\phi_1(x)dx&\int\phi_2^*(x)\hat{O}\phi_2(x)dx&\cdots\\\vdots&\vdots&\ddots\end{array}\right)\tag{19}\] のように表すことができるだろう。成分表示するなら、 \[a_{mn}=\int\phi_m^*(x)\hat{O}\phi_n(x)dx\tag{20}\] となる。5.行列から演算子を作り出す
演算子↔行列という対応関係を考えているのだから、行列から演算子を作り出すこともできないといけない。それについて少し考えてみよう。こっち側は直感的な説明がしにくかったので、少し数学的になってしまった。ベクトル表示した関数\(f\)と\(g\)の間に\(g=Af\)という関係があるとしよう。これは関数によって表記すると、 \begin{align} g(x)&=\sum_m g_m\phi_m(x) \\ &=\sum_m\left(\sum_n a_{mn}f_n\right)\phi_m(x)\\ &=\sum_m\sum_na_{mn}f_n\phi_m(x)\tag{21} \end{align} とできる。このとき、\(g(x)=\hat{O}_Af(x)\)となるような演算子\(\hat{O}_A\)を見つけたい。どうしたらいいだろうか。
\(g(x)=\hat{O}_Af(x)\)という形を作れればいいのだが、(21)には\(f(x)\)が含まれていない。そこで、係数\(f_n\)が \[f_n=\int \phi^*_n(x) f(x)dx\] と求められていたことを思い出そう。それで、これを代入してみる。すると、 \begin{align} g(x)&=\sum_m\sum_na_{mn}\left(\int \phi^*_n(x') f(x')dx'\right)\phi_m(x)\\ &=\int\left(\sum_m\sum_n\phi_m(x)a_{mn}\phi^*_n(x')\right) f(x')dx' \end{align} つまり、「\(\sum_m\sum_n\phi_m(x)a_{mn}\phi^*_n(x')\)という関数をかけて積分する」という演算子が求めたかった演算子\(\hat{O}\)である。露わに書くことが少しむずかしいが、つまり、 \[\hat{O}f(x)=\int\left(\sum_m\sum_n\phi_m(x)a_{mn}\phi^*_n(x')\right) f(x')dx'\] という意味である。
6.まとめ
演算子→行列は次のようにする。 \[a_{mn}=\int\phi_m^*(x)\hat{O}\phi_n(x)dx\tag{22}\] 行列→演算子は少し書き表しにくいが、行列\(A\)に対応する演算子\(\hat{O}\)は関数にかけたときに次のような働きをするものだ。 \[\hat{O}f(x)=\int\left(\sum_m\sum_n\phi_m(x)a_{mn}\phi^*_n(x')\right) f(x')dx'\tag{23}\] これは、\(K(x,x')=\sum_m\sum_n\phi_m(x)a_{mn}\phi^*_n(x')\)という関数を定義してもう少しわかりやすく書ける。 \[\hat{O}f(x)=\int K(x,x')f(x')dx'\] となる。7.行列の積・演算子の積
最後に、演算子の積や行列の積に対応関係があるか考えておこう。演算子\(\hat{A},\hat{B}\)の積の演算子\(\hat{C}=\hat{A}\hat{B}\)に対応する行列\(C\)は、\(\hat{A},\hat{B}\)に対応する行列\(A,B\)の積になっているだろうか?
まあ考えてみよう。まず、 \begin{align} C_{mn}&=\int\phi_m^*(x)\hat{C}\phi_n(x)dx\\ &=\int\phi_m^*(x)\hat{A}\hat{B}\phi_n(x)dx\tag{24} \end{align} はいい。ここで \[B_{mn}=\int\phi_m^*(x)\hat{B}\phi_n(x)dx\] だから、この式の見方を少し変えて、 \[B_{mn}=\int\phi_m^*(x)\left(\hat{B}\phi_n(x)\right)dx\] とみると、\(B_{mn}\)というのは\(\hat{B}\phi_n(x)\)という関数を\(\phi_m\)によって展開したときの係数になっている。したがって、 \[\hat{B}\phi_n(x)=\sum_mB_{mn}\phi_m\tag{25}\] が成り立つ。(24)に代入して、 \begin{align} C_{mn}&=\int\phi_m^*(x)\hat{A}\left(\sum_kB_{kn}\phi_k\right)dx \\ &=\sum_kB_{kn}\int\phi_m^*(x)\hat{A}\phi_k(x)dx\\ &=\sum_kB_{kn}A_{mk}\\ &=\sum_kA_{mk}B_{kn} \end{align} つまり、 \[C=AB\] が成り立っていることが言えた。演算子の和については行列の和で表せることはすぐに示せるから、とりあえず演算子の普通の計算については、行列計算によって置き換えることができることがわかったわけだ。