生成演算子と消滅演算子を使って調和振動子を解く
1.調和振動子のシュレディンガー方程式
調和振動子のハミルトニアンは、古典力学で以下の形で与えられる。 \[H(x,p)=\frac{p^2}{2m}+\frac{m\omega^2x^2}{2}\tag{1}\] これまで説明してきたように、古典論のハミルトニアンがあったとき、量子力学の波動関数\(\psi\)は以下のシュレディンガー方程式 \[\hat{H}(\hat{x},\hat{p})\psi=E\psi\tag{2}\] を満たすものとして求められるのだった。(1)のハミルトニアンを使って、(2)をしっかりと書いてやると \[\left(\frac{\hat{p}^2}{2m}+\frac{m\omega^2\hat{x}^2}{2}\right)\psi=E\psi\tag{3}\] となる。で、例えば位置演算子として\(\hat{x}=x\)、運動量演算子として\(\hat{p}=-i\hbar\partial_x\)をとると、(3)の解は \[\phi_n(x) = A_n~H_n\left(\sqrt\frac{m\omega}{\hbar}x\right)\exp\left(-\frac{m\omega}{2\hbar}x^2\right)\tag{4}\] \[E_n = \hbar\omega\left(n+\frac{1}{2}\right)\tag{5}\] という形で書くことができた。図を書くと下のようになる。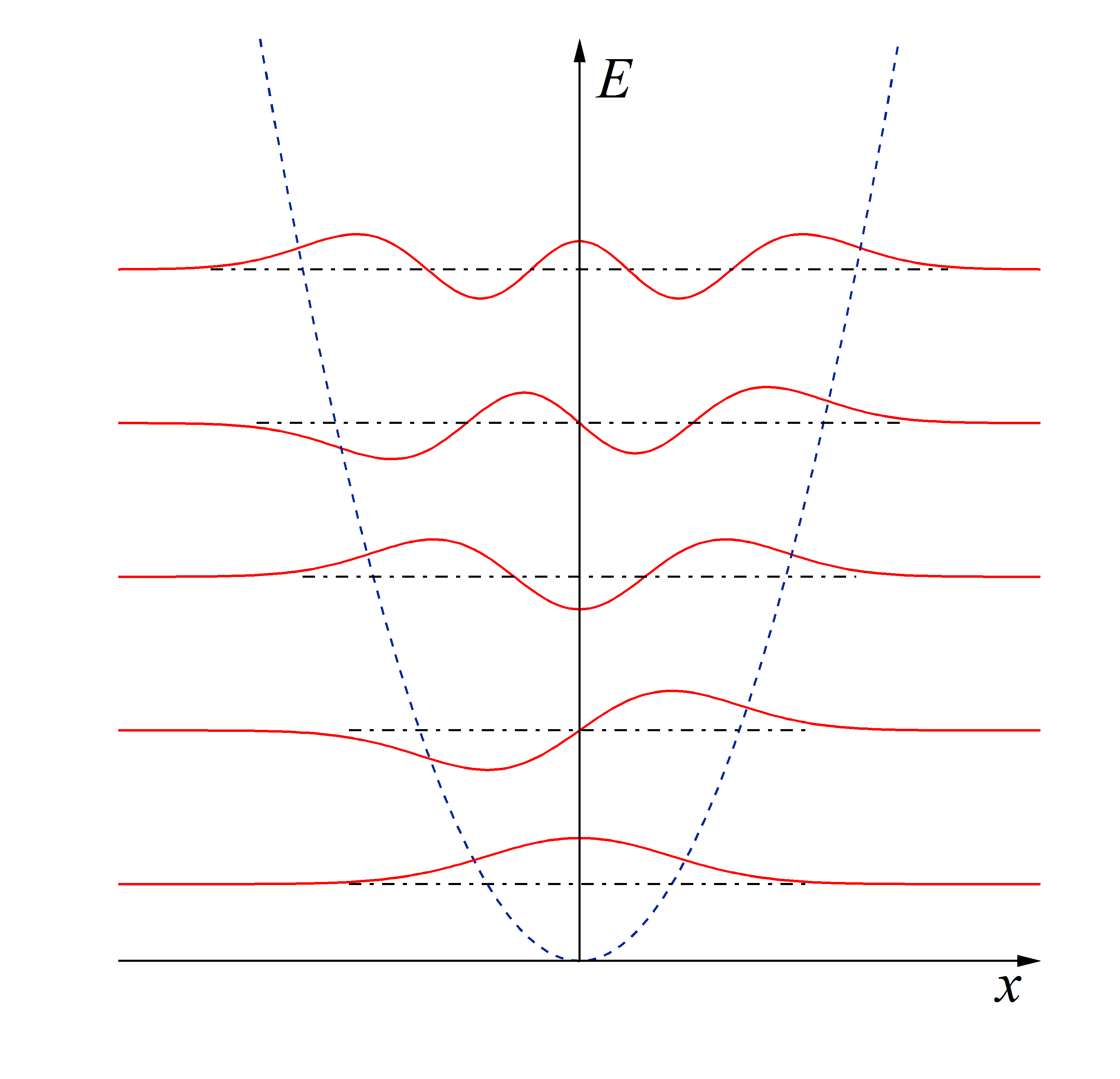
2.ちょっとした工夫
しかしそのままやろうとしても行列力学で調和振動子を解いたときのように、わけのわからない計算を延々とやらなくちゃいけないのは目に見えている。そこでディラックがやったように工夫して解いてみよう。まずハミルトニアンを形式的に因数分解してみよう。 \[\hat{H}(\hat{x},\hat{p})=\frac{m\omega^2\hat{x}^2}{2}+\frac{\hat{p}^2}{2m}\] だったから、普通の因数分解\(a^2-b^2=(a+b)(a-b)\)を使ってみると \[\hat{H}(\hat{x},\hat{p})?= \left(\sqrt{\frac{m}{2}}\omega\hat{x}+i\frac{\hat{p}}{\sqrt{2m}}\right)\left(\sqrt{\frac{m}{2}}\omega\hat{x}-i\frac{\hat{p}}{\sqrt{2m}}\right)\tag{6}\] しかし、この式は正しくない。それは\(\hat{x},\hat{p}\)が交換しないからだ。(6)式のような因数分解の形を使って、もとのハミルトニアンを再現するには、次のようにすればいい。 \[\hat{H}(\hat{x},\hat{p})= \frac{1}{2}\left(\sqrt{\frac{m}{2}}\omega\hat{x}+i\frac{\hat{p}}{\sqrt{2m}}\right)\left(\sqrt{\frac{m}{2}}\omega\hat{x}-i\frac{\hat{p}}{\sqrt{2m}}\right) + \frac{1}{2}\left(\sqrt{\frac{m}{2}}\omega\hat{x}-i\frac{\hat{p}}{\sqrt{2m}}\right)\left(\sqrt{\frac{m}{2}}\omega\hat{x}+i\frac{\hat{p}}{\sqrt{2m}}\right)\] したがって、演算子\(\hat{a}\)を \[\hat{a}=\sqrt{\frac{m\omega}{2\hbar}}\hat{x}+i\frac{\hat{p}}{\sqrt{2m\hbar\omega}}\tag{7}\] と定義すれば \[\hat{H}=\frac{\hbar\omega}{2}(\hat{a}\hat{a}^\dagger+\hat{a}^\dagger\hat{a})\tag{8}\] とあらわせることになる。\(\hbar\omega\)をくくりだしたのは、\(\hat{H}\)の次元がエネルギーであることを明らかにするためだ。
さて、この\(\hat{a},\hat{a}^\dagger\)を使って調和振動子を解いていく。
3.\(\hat{a},\hat{a}^\dagger\)の性質
まずはこれらの演算子の性質を調べていく。交換関係を色々と調べてみよう。\([\hat{a},\hat{a}^\dagger]\)は、 \begin{align} [\hat{a},\hat{a}^\dagger] &= \hat{a}\hat{a}^\dagger - \hat{a}^\dagger\hat{a}\\ &= \left(\sqrt{\frac{m}{2}}\omega\hat{x}+i\frac{\hat{p}}{\sqrt{2m}}\right)\left(\sqrt{\frac{m}{2}}\omega\hat{x}-i\frac{\hat{p}}{\sqrt{2m}}\right) - \frac{1}{2}\left(\sqrt{\frac{m}{2}}\omega\hat{x}-i\frac{\hat{p}}{\sqrt{2m}}\right)\left(\sqrt{\frac{m}{2}}\omega\hat{x}+i\frac{\hat{p}}{\sqrt{2m}}\right)\\ &=\left( \frac{m\omega}{2\hbar}\hat{x}^2 + \frac{\hat{p}^2}{2m\hbar\omega} +\frac{i}{2\hbar}\hat{p}\hat{x} - \frac{i}{2\hbar}\hat{x}\hat{p} \right) -\left( \frac{m\omega}{2\hbar}\hat{x}^2 +\frac{\hat{p}^2}{2m\hbar\omega} -\frac{i}{2\hbar}\hat{p}\hat{x} + \frac{i}{2\hbar}\hat{x}\hat{p} \right)\\ &=-\frac{i}{\hbar}[\hat{x},\hat{p}] \end{align} で、最後に\([\hat{x},\hat{p}] = i\hbar\)の交換関係から、 \[[\hat{a},\hat{a}^\dagger] = 1 \] を得る。これがかなり基本となる関係式である。じゃあ次にハミルトニアンとの交換関係を計算してみる。この交換関係から、ハミルトニアンは\(\hat{H}=\hbar\omega(\hat{a}\hat{a}^\dagger-\frac{1}{2})\)とも表せるから、 \begin{align} [\hat{a},\hat{H}] &= \hbar\omega\left[\hat{a},\hat{a}\hat{a}^\dagger -\frac{1}{2}\right]\\ &=\hbar\omega\left(\left[\hat{a},\hat{a}\hat{a}^\dagger\right] - \left[\hat{a},\frac{1}{2}\right]\right) \\ &=\hbar\omega\left[\hat{a},\hat{a}\hat{a}^\dagger\right]\\ &=\hbar\omega(\hat{a}\hat{a}\hat{a}^\dagger-\hat{a}\hat{a}^\dagger\hat{a})\\ &=\hbar\omega\hat{a}(\hat{a}\hat{a}^\dagger-\hat{a}^\dagger\hat{a})\\ &=\hbar\omega\hat{a}[\hat{a},\hat{a}^\dagger]\\ &=\hbar\omega\hat{a} \end{align} となった。ということは、これのダガーをとって、 \[[\hat{H},\hat{a}^\dagger]=\hbar\omega\hat{a}^\dagger\] も成り立つ。まとめると、 \[\left\{\begin{align} [\hat{a},\hat{a}^\dagger] &= 1\\ [\hat{a},\hat{H}] &= \hbar\omega\hat{a}\\ [\hat{a}^\dagger,\hat{H}] &= -\hbar\omega\hat{a}^\dagger \end{align}\right.\tag{11} \] となった。
4.解いていく
まず、ハミルトニアン\(\hat{H}\)について固有状態\(\ket{n}\)があって、 \[\hat{H}\ket{n}=E_n\ket{n}\tag{12}\] となっていたと仮定する。この\(\ket{n}\)に\(\hat{a}\)を作用させたものがどのような状態になっているか調べるために、\(\hat{H}(\hat{a}\ket{n})\)というのを計算してみよう。(11)の真ん中の交換関係を使う。 \begin{align} \hat{H}(\hat{a}\ket{n}) &= (\hat{a}\hat{H}-\hbar\omega\hat{a})\ket{n} \\ &= \hat{a}\hat{H}\ket{n}-\hbar\omega\hat{a}\ket{n} \\ &= \hat{a}E_n\ket{n}-\hbar\omega\hat{a}\ket{n} \\ &= (E_n-\hbar\omega)(\hat{a}\ket{n}) \end{align} \(\hat{a}^\dagger\)についても同様な計算を行うことができる。まとめて書いておくと、 \begin{align} \hat{H}(\hat{a}\ket{n})&= (E_n-\hbar\omega)(\hat{a}\ket{n})\tag{13}\\ \hat{H}(\hat{a}^\dagger\ket{n})&= (E_n+\hbar\omega)(\hat{a}^\dagger\ket{n})\tag{14} \end{align} となる。これが意味するところを考えよう。最初の式は、\(\hat{a}\ket{n}\)という状態にハミルトニアンをかけたら、\(\hat{a}\ket{n}\)のある定数倍になっているという式だ。ということはこの\(\hat{a}\ket{n}\)という状態はハミルトニアンの固有状態であり、そのエネルギー固有値は、もとの\(\ket{n}\)よりも\(\hbar\omega\)だけ少ない\(E_n-\hbar\omega\)だ。下の式も\(\hat{a}^\dagger\ket{n}\)について同様のことを言っている。
さて、これで\(\hat{a}\)でエネルギーが小さい状態を作り出せて、\(\hat{a}^\dagger\)ではエネルギーの大きい状態を作り出せることがわかったのだが、エネルギーに最小値や最大値はあるのだろうか。
そこでこんなことを考えてみよう。\(\hat{a}\ket{n}\)の長さを調べるのだ。長さというのは実数でしかも正でないといけないから、その条件から最大値や最小値の条件を見つけることができるかもしれない。
\(\hat{a}\ket{n}\)の長さはそれ自身と内積を取ればいい。それが0以上になるというのだから、次のように計算していける。 \begin{align} \bra{n}\hat{a}^\dagger\hat{a}\ket{n}&\geq 0 \\ \bra{n}\left(\frac{\hat{H}}{\hbar\omega}-\frac{1}{2}\right)\ket{n}&\geq 0\\ \frac{\bra{n}\hat{H}\ket{n}}{\hbar\omega}-\frac{1}{2}\braket{n}{n}&\geq 0\\ \frac{\bra{n}E_n\ket{n}}{\hbar\omega}-\frac{1}{2}&\geq 0\\ \frac{E_n\braket{n}{n}}{\hbar\omega}-\frac{1}{2}&\geq 0\\ \frac{E_n}{\hbar\omega}-\frac{1}{2}&\geq 0\\ E_n&\geq \frac{\hbar\omega}{2} \end{align} \(\hat{H}=\hbar\omega(\hat{a}^\dagger\hat{a}+\frac{1}{2})\)を一行目から二行目に行くときに使った。それ以外は別に問題無いと思う。
ということで、\(E_n\)というのはかならず\(\hbar\omega/2\)以上であることがわかった。では最小値は\(\hbar\omega/2\)だろうか?そうではないだろうか?
とりあえず\(E_{\text{min}}\neq\hbar\omega/2\)と仮定してみる。そして、この最小エネルギー状態を\(\ket{\text{min}}\)とでも書くことにしよう。もちろんこのとき\(E_{\text{min}}\gt\hbar\omega/2\)が成り立っているから、状態\(\ket{\text{min}}\)は今やった計算を逆にたどれば、 \[\bra{\text{min}}\hat{a}^\dagger\hat{a}\ket{\text{min}}\gt 0\] を満たしていることを示せる。これはつまり、\(\hat{a}\ket{\text{min}}\)というベクトルが0でない長さをもっていることを意味していて、 \[\hat{a}\ket{\text{min}}\neq 0\] だということだ。しかし、\(\hat{a}\ket{\text{min}}\)という状態は、\(\ket{\text{min}}\)よりも\(\hbar\omega\)だけ小さいエネルギーをもつ状態を表すのだった。これでは\(\ket{\text{min}}\)が最小エネルギー状態だということと矛盾する。
\(E_{\text{min}}\neq\hbar\omega/2\)を仮定したら矛盾したので、この仮定が間違っている以外にはありえない。つまり、\(E_{\text{min}}=\hbar\omega/2\)である。
実際これなら、 \[\bra{\text{min}}\hat{a}^\dagger\hat{a}\ket{\text{min}}= 0\] となり、つまり\(\hat{a}\ket{\text{min}}=0\)となるのだ。つまり最小エネルギー状態よりも小さいエネルギー状態を作り出そうとしても、その状態は消えてしまうのだ。
5.まとめ
最小エネルギーが \[E_{\text{min}}=\frac{\hbar\omega}{2}\] であることがわかった。あとはこの最小エネルギーをとる状態から、(14)式を使って、\(\hat{a}^\dagger\)によって順々にエネルギーを増やしていけばすべてのエネルギー状態を作り出すことができるだろう。 (このように作り出した状態が、調和振動子のすべての状態を網羅している。もし他のエネルギー状態があるとすると、エネルギーがかならず\(\hbar\omega/2\)以上であるという条件を満たさなくなってしまう。)したがって、調和振動子のエネルギー準位は \[E_n=\hbar\omega\left(n+\frac{1}{2}\right)\] であるといえる。
このように、純粋に代数的な関係のみで、エネルギー準位を見つけることができるのだが、結構不思議だ。シュレディンガー方程式を微分方程式として解く場合には、無限遠で波動関数が0になるという「境界条件」からエネルギー準位が上のようになることが示されるのに。交換関係にそういうこと (境界条件) まで含まれているとでも言うのだろうか。
実はそういうことではない。別に交換関係に境界条件が含まれているわけではないのだ。
このページでやったような演算子のみで解く方法というのは、電子を粒子的にとらえて解いているのである。そして交換関係は、ボーアの量子条件に相当する役割を果たす。しかし今回のような計算をしてみると、粒子的に捉えて解く方法というのは、概して直感性を失いやすいものなのかもしれない。