N個のスピン1/2系の角運動量の合成

---

1. 導入

今回は、スピン量子数\(s=1/2\)であるような粒子が\(N\)個集まった系の、全角運動量演算子の大きさ\(S^2\)と、全角運動量の\(z\)成分\(S_z\)に関する同時固有状態をどのように構成するか説明してみようと思う。この問題は角運動量の合成の問題としても馴染み深いだろう。しかし\(N\)個の粒子の合成となると、あまり情報が見つからなかったので、書いてみようと思った次第である。

また、スピン1/2の粒子を考えることは2準位系を考えることと等価なので、一般に2つの状態を持つ量子系を\(N\)個用意すれば同じような議論が展開できる。具体的な応用先として、例えば量子コンピュータの物理の解析なんかに使えることがあるかもしれない。なぜなら量子コンピュータは非常にたくさんの2準位系 (= qubit) の集まりだからだ。他にもスピンを直接扱うNMR実験なんかはもちろんのこと、光子の偏光状態を用いた量子通信なんかにも応用できるんじゃないかな。

さて、さっそくやってみよう。今回は一般的な角運動量演算子の基本的な性質については既知とする。

---

---

2. 文字の定義とか

まずは一般的な角運動量演算子\(\b{L} = (L_{x},~L_{y},~L_{z})\)の性質についてまとめておく。角運動量演算子の\(x,y,z\)成分は \[[L_{x},L_{y}] = iL_{z},~[L_{z},L_{x}] = iL_{y},~[L_{y},L_{z}] = iL_{x}\tag{1}\] という交換関係を満たす。(今回\(\hbar\)は\(1\)とする。) また、角運動量の大きさを表す演算子\(L^2 = L_x^2+L_y^2+L_z^2\)と角運動量の1つの成分、例えば\(z\)方向成分\(L_z\)が可換であり、この2つの演算子の固有値を指定すると、角運動量状態が1つに定まる。一般に、\(L^2\)の固有値は\(l(l+1)\) (\(l\)は\(n/2\) \((n=1,2,3,\cdots)\)の形で表される数)、\(L_z\)の固有値は\(m\) (\(\{m\}\)は\(|m|\leq l\)を満たし、それぞれの差が1の数) と書くことが可能である。慣例にならって、\(L^2\), \(L_z\)に関してそれぞれ固有値\(l(l+1),~m\)を持つ状態を\(\ket{l,m}\)と書くことにしよう。つまり、 \[L^2\ket{l,m} = l(l+1)\ket{l,m},~~L_z\ket{l,m} = m\ket{l,m}\tag{2}\] である。

また、昇降演算子というのもここで準備しておく。昇降演算子は、一般の角運動量演算子に対して、 \[l_{\pm} = l_{x} \pm il_{y} \tag{3}\] と定義される演算子であり、\(l_z\)との交換関係は \[[l_{z},l_{+}]=l_{+},~[l_{z},l_{-}]=-l_{-}\] である。この演算子は、\(\ket{l,m}\)に作用した時、\(l_z\)の固有値\(m\)を+1したり-1したりする働きをする。一方で\(\b{l}^2\)とは可換であって、その固有値\(l\)は変化させない。具体的に式で書くと、 \[\begin{align} l_{+}\ket{l,m} = \sqrt{l(l+1)-m(m+1)}\ket{l,m+1} \\ l_{-}\ket{l,m} = \sqrt{l(l+1)-m(m-1)}\ket{l,m-1} \end{align} \tag{4}\] である。前についている\(\sqrt{l(l+1)-m(m+1)}\)の因子は状態の規格化のためのものであり、それほど大きな意味はない。大切なのは、\(l_{\pm}\)が\(l\)を変えずに\(m\)だけを増減させる演算子であることだ。

さて、今回はスピン1/2が\(N\)個ある系を考えるので、各スピンの演算子を定義しておこう。\(i\)番目のスピン演算子を \[\b{s}_i = (s_{ix},~s_{iy},~s_{iz}) \tag{5}\] とする。これは角運動量演算子なので、当然 \[[s_{ix},s_{iy}] = is_{iz},~[s_{iz},s_{ix}] = is_{iy},~[s_{iy},s_{iz}] = is_{ix}\tag{6}\] という交換関係を満たす。さらに今回考えるのはスピン1/2なので、それぞれの\(s_z\)は2つの固有値\(\pm1/2\)だけを持つ。固有値\(+1/2\)に対応する\(s_z\)の固有状態を\(\ket{0}\)、\(-1/2\)に対応する固有状態は\(\ket{1}\)と書くことにしよう。また、スピン1/2の演算子は、この\(\ket{0}, \ket{1}\)を基底とし、 \[\ket{0}\to\left(\begin{array}{c}1\\0\end{array}\right),~\ket{1}\to\left(\begin{array}{c}0\\1\end{array}\right)\] とベクトルと結びつけたとき、次のような行列として書きあらわせる。 \begin{align} s_x&= \frac{1}{2}\left(\begin{array}{cc}0&1\\1&0\end{array}\right),& s_y&= \frac{1}{2}\left(\begin{array}{cc}0&-i\\i&0\end{array}\right),& s_z&= \frac{1}{2}\left(\begin{array}{cc}1&0\\0&-1\end{array}\right) \tag{7} \end{align} この行列表現からもわかるように、 \[s_x^2 = s_y^2 = s_z^2 = \frac{I}{4} \tag{8}\] が成り立つ。\(I\)は恒等演算子、もしくは単位行列である。

また、全角運動量演算子\(\b{S}\)は \[\b{S} = \sum_i \b{s}_i \tag{9}\] と定義する。そこまで当たり前にも思えないかもしれないが、この全角運動量演算子\(\b{S}\)の各成分の間にも \[[S_{x},S_{y}] = iS_{z},~[S_{z},S_{x}] = iS_{y},~[S_{y},S_{z}] = iS_{x} \tag{10}\] という交換関係が成立し、\(\b{S}\)も角運動量演算子としての性質を全て満たす。

次に、\(N\)個のスピンの状態を書き表す方法を定義する。例えば1番目のスピンが\(\ket{0}_1\), 2番目のスピンが\(\ket{1}_2\)、...、\(N\)番目のスピンが\(\ket{0}_N\)であるような状態を表すには、単にこれらを並べて、 \[\ket{0}_1\ket{1}_2\cdots\ket{0}_N\] と表すことにする。

これで記号の定義は終わりにして、今回の目標をここでまとめておこう。 \(\ket{0}_1\ket{1}_2\cdots\ket{0}_N\)のような状態は\(S_z\)の固有状態になってはいるが、実は一般に\(S^2\)の固有状態とはならないので、こういう問題が現れるのだ。

---

3. 2スピン状態の構成

まずは簡単に、2スピンの系で、\(S^2\)と\(S_z\)に対する同時固有状態を構成してみる。

\(S_z\)に対して、１番大きな固有値を持っていそうなのは、それぞれのスピンが\(+1/2\)の固有値を持つ\(\ket{0}\)の状態にいるものだろう。その固有値も\(1/2\)が２つあるのだから、\(1\)になることが予想される。実際この状態\(\ket{0}_1\ket{0}_2\)に\(S_z=s_{1z} + s_{2z}\)を作用させると、 \begin{align} S_z\ket{0}_1\ket{0}_2 &= (s_{1z} + s_{2z})\ket{0}_1\ket{0}_2 \\ &= s_{1z} \ket{0}_1\ket{0}_2 + s_{2z} \ket{0}_1\ket{0}_2 \\ &= \frac{1}{2} \ket{0}_1\ket{0}_2 + \frac{1}{2}\ket{0}_1\ket{0}_2 \\ &= \ket{0}_1\ket{0}_2 \end{align} となる。計算に際しては、\(s_{z1}\)は1番目のスピン状態だけに作用する状態であり、2番目のスピン状態には何もしないことに注意しよう。逆も同じである。この結果からわかるように、\(\ket{0}_1\ket{0}_2\)は確かに\(S_z\)に対して\(1\)という固有値をもつ。

実はこの状態は\(S^2\)の固有状態にもなっている。2スピンの場合\(S^2\)は、 \begin{align} S^2 &= (s_{1x}+s_{2x})^2 + (s_{1y}+s_{2y})^2 + (s_{1z}+s_{2z})^2 \\ &= s_{1x}^2 + s_{2x}^2 + s_{1y}^2+s_{2y}^2 + s_{1z}^2+s_{2z}^2 + 2s_{1x}s_{2x} + 2s_{1y}s_{2y} + 2s_{1z}s_{2z} \\ &= \frac{3}{2}I + 2(s_{1x}s_{2x} + s_{1y}s_{2y} + s_{1z}s_{2z}) \\ \end{align} と表せるから、これを\(\ket{0}_1\ket{0}_2\)に作用させて確かめてみよう。 \begin{align} s_x\ket{0} &= \frac{1}{2}\ket{1},& s_y\ket{0} &= \frac{i}{2}\ket{1},& s_z\ket{0} &= \frac{1}{2}\ket{0} \end{align} に注意して、 \begin{align} S^2 &= \frac{3}{2}\ket{0}_1\ket{0}_2 + 2s_{1x}s_{2x}\ket{0}_1\ket{0}_2 + 2s_{1y}s_{2y}\ket{0}_1\ket{0}_2 + 2s_{1z}s_{2z}\ket{0}_1\ket{0}_2 \\ &= \frac{3}{2}\ket{0}_1\ket{0}_2 + \frac{1}{2}\ket{1}_1\ket{1}_2 - \frac{1}{2}\ket{1}_1\ket{1}_2 + \frac{1}{2} \ket{0}_1\ket{0}_2 \\ &= 2\ket{0}_1\ket{0}_2 \end{align} となる。確かに\(\ket{0}_1\ket{0}_2\)は\(S^2\)の固有状態であることがわかった。さらにその固有値が\(2\)であるということは、(2)式と照らし合わせてこの状態が\(l=1\)の状態に対応していることがわかる。

これらのことから、 \[\ket{l=1,m=1} = \ket{0}_1\ket{0}_2\tag{11}\] であると結論できる。これがわかってしまえば、\(\ket{l=1,m=0}\), \(\ket{l=1,m=-1}\)の状態を構成するのは簡単だ。(4)式に注意しながら\(S_-\)をかければ良いだけである。 \[S_- = s_{1-}+s_{2-}\] なので、これを(11)に掛けて、 \begin{align} S_-\ket{l=1,m=1} &= (s_{1-}+s_{2-})\ket{0}_1\ket{0}_2 \\ \sqrt{2}\ket{l=1,m=0} &= s_{1-}\ket{0}_1\ket{0}_2 + s_{2-}\ket{0}_1\ket{0}_2 \\ \ket{l=1,m=0} &= \frac{1}{\sqrt{2}}(\ket{1}_1\ket{0}_2 + \ket{0}_1\ket{1}_2) \tag{12} \end{align} を得る。さらにもう一度\(S_-\)をかければ、途中計算は省くが、 \[\ket{l=1,m=-1} = \ket{1}_1\ket{1}_2 \tag{13}\] が得られる。

さて、これで\(l=1\)の状態としてそれぞれ直交する状態が3つ構成できた。でももう一度最初にもどって考えてみると、2つのスピン1/2があるときには、 \[\ket{0}_1\ket{0}_2,~~\ket{0}_1\ket{1}_2,~~\ket{1}_1\ket{0}_2,~~\ket{1}_1\ket{1}_2\] という4通りの状態 (基底) が存在するはずである。しかしながら、ここまでに構成した\(l=1\)の状態だけでは、3つしか現れていないので、これだけでは基底を構成することはできない。そこで、正規直交基底を作ることを念頭に置いて、これまでの3状態に直交する状態を考えてみよう。少し考えればわかると思うが、それは \[\frac{1}{\sqrt{2}}(\ket{1}_1\ket{0}_2 - \ket{0}_1\ket{1}_2)\] という状態である。実はこれが嬉しいことに、\(S^2\)と\(S_z\)の固有状態になっているのだ。ここまでで計算例は十分書いたと思うから、途中計算は省いてしまうが、掛けてみればわかるように、この状態は\(S^2\)、\(S_z\)のどちらについても\(0\)の固有値をもつ固有状態である。したがって、 \[\ket{l=0,m=0} = \frac{1}{\sqrt{2}}(\ket{1}_1\ket{0}_2 - \ket{0}_1\ket{1}_2)\tag{14}\] と結論できる。

2スピンの場合についてまとめよう。みやすさを優先して、ここからは\(\ket{l=0,m=0}\)を\(\ket{0,0}\)のように書くことにする。

---

4. 物理的解釈

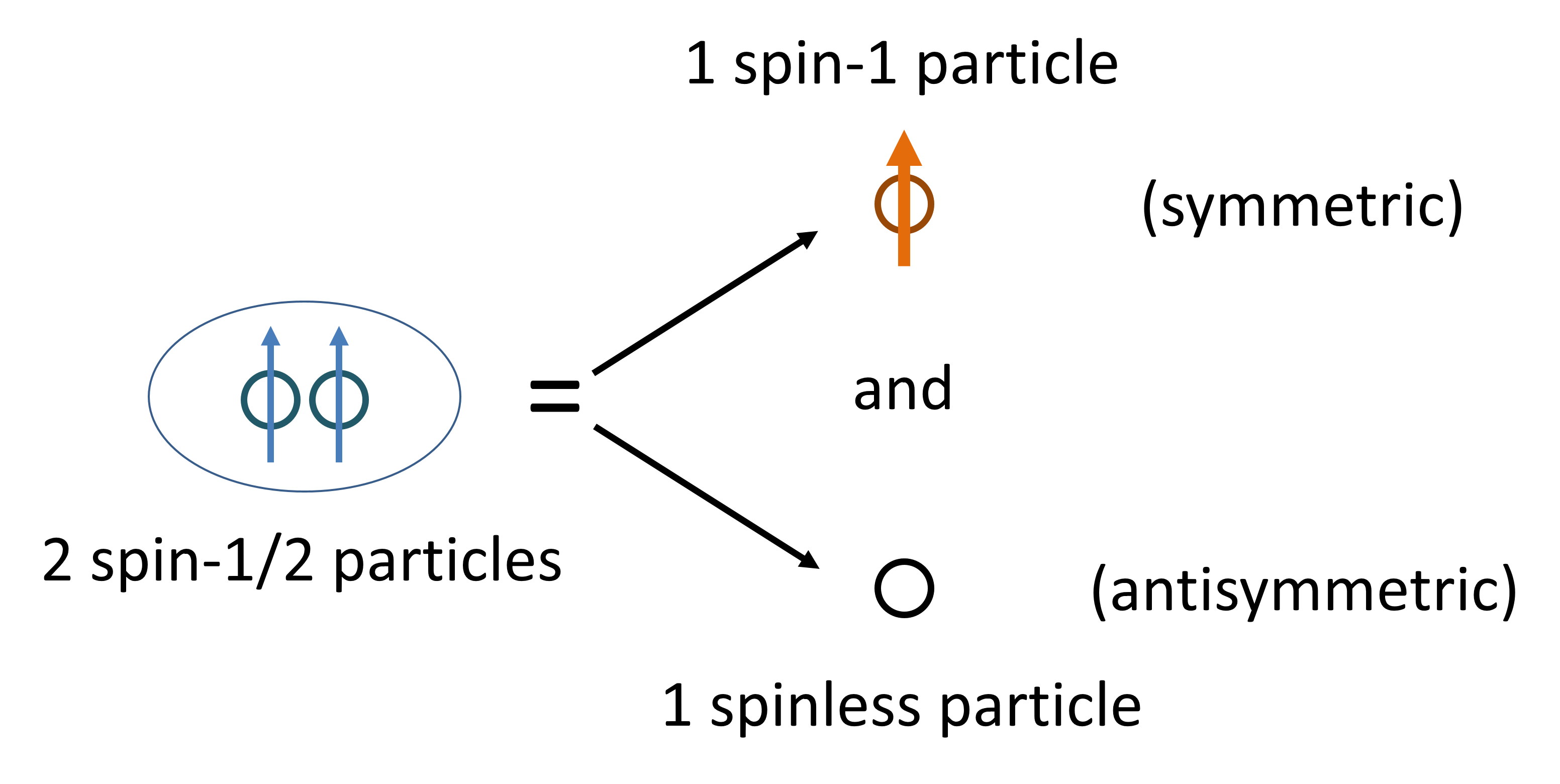
これで2スピンの場合について\(\ket{l,m}\)が構成できたわけだが、3スピンの場合に進む前に、上に現れた状態の物理的意味について少し説明しておこうと思う。

「全」角運動量演算子の大きさ\(S^2\)とz成分\(S_z\)に関する固有状態を考えるということは、2つのスピンを2つのものとして分離せず、完全に1つの系として考えるということである。本当は2つの粒子なのだけども、それを1つの粒子とみなしてその性質を調べている、と言ってもいい。

上で導出した2スピンの状態のうち、\(l=0\)の状態は、2つのスピンをあわせて見たときに、その全角運動量が\(0\)、つまり全体では全く「回転」していない状態である。逆に\(l=1\)の状態は全角運動量の大きさが\(0\)では無く、ある方向を回転軸として回転している状態だ。したがって、\(\ket{l,m}\)を構成したことによって、2つのスピンの空間を、回転している3つの状態\(\ket{1,1},\ket{1,0},\ket{1,-1}\)と、回転していない状態\(\ket{0,0}\)に、ある意味「分離」できたと言える。物理的な性質から見れば、\(l=1\)の状態はスピン1の粒子と同一視できるし、\(l=0\)の状態はスピンの無い状態と同一視できる。そこで以下の図のような描像が成り立つだろう。 この描像は3スピン以上の\(\ket{l,m}\)状態を構成するのに役に立つ。

---

5. 3スピンの場合

さて、次は3スピンの場合について考えよう。

わざわざ説明したことからも予想がつくかもしれないが、2スピンで構成した\(\ket{l,m}\)を使って構成する。

まず、2スピンで\(l=0\)の状態に、スピン1/2を付け足すことを考えてみよう。この場合、そもそも前から存在した2つのスピンが合わさって全くスピンを持っていない状態なのだから、もう一つのスピン1/2を付け足すと、その全体のスピンの大きさは、付け足したスピンのものと全く同じになると考えられる。そのことを確かめるために、 \[\ket{0,0}_{1,2}\ket{0}_3,~~\ket{0,0}_{1,2}\ket{1}_3\] という状態を考えてみよう。\(S_z\)の固有状態となっていることは明らかだろうと思うので、\(S^2\)を考えよう。1,2番目のスピンに対する全角運動量演算子を\(\b{S}_{12}=\b{s}_1+\b{s}_2\)とすると、\(S^2\)は3スピンの場合 \begin{align} S^2 &= (S_{12x}+s_{3x})^2 + (S_{12y}+s_{3y})^2 + (S_{12z}+s_{3z})^2 \\ &= S_{12}^2+ \frac{3}{4}I+ 2 (S_{12x}s_{3x}+S_{12y}s_{3y} + S_{12z}s_{3z}) \end{align} となる。\(\ket{0,0}_{1,2}\)は「回っていない」状態だったので、\(\b{S}_{12}\)のどの成分が\(\ket{0,0}\)に作用したとしても、その結果は\(0\)である。

ほんと？と思った人のための補足。\(S_{12x}\)や\(S_{12y}\)を\(S_{12+}\)と\(S_{12-}\)に分解してやればわかりやすいと思う。例えば\(S_{12x}=(S_{12+}+S_{12-})/2\)であるが、昇降演算子は\(m\)を\(|m|\leq l\)となる範囲で増減させる演算子なのだから、\(\ket{0,0}_{1,2}\)に対してはどちらも\(0\)になって消えてしまうのだ。

したがって、\(S^2\)を\(\ket{0,0}_{1,2}\ket{0}_3\)や\(\ket{0,0}_{1,2}\ket{1}_3\)に作用させた結果は、 \begin{align} S^2\ket{0,0}_{1,2}\ket{0}_3 &= \frac{3}{4}\ket{0,0}_{1,2}\ket{0}_3 \\ S^2\ket{0,0}_{1,2}\ket{1}_3 &= \frac{3}{4}\ket{0,0}_{1,2}\ket{1}_3 \end{align} である。また、計算は省くが\(S_z\)に対しては固有値\(\pm1/2\)を持つ。このことから、これらの状態が\(S^2\)と\(S_z\)に対する同時固有状態であり、 \begin{align} \ket{\frac{1}{2},\frac{1}{2}}_{1,2,3} &= \ket{0,0}_{1,2}\ket{0}_3 = \frac{1}{\sqrt{2}}(\ket{1}_1\ket{0}_2 - \ket{0}_1\ket{1}_2)\ket{0}_3 \\ \ket{\frac{1}{2},-\frac{1}{2}}_{1,2,3} &= \ket{0,0}_{1,2}\ket{1}_3 = \frac{1}{\sqrt{2}}(\ket{1}_1\ket{0}_2 - \ket{0}_1\ket{1}_2)\ket{1}_3 \end{align} と書けることがわかる。

次に\(l=1\)の状態との合成を考えよう。\(l=1\)の場合、スピン1の粒子と同一視できたのだから、この状態にスピン1/2の粒子を付け足すということは、スピン1の粒子とスピン1/2の粒子が合わさった系を考えることと同じである。この合成のやり方は、角運動量の合成のページで取り上げたものになるので、計算の詳細はそっちを参照してほしい。結果は次のようになる。

\(l=3/2\)のもの： \begin{align} \ket{\frac{3}{2},\frac{3}{2}}_{1,2,3}&=\ket{1,1}_{1,2}\ket{0}_3\\ \ket{\frac{3}{2},\frac{1}{2}}_{1,2,3}&=\sqrt{\frac{2}{3}}\ket{1,0}_{1,2}\ket{0}_3 + \frac{1}{\sqrt{3}}\ket{1,1}_{1,2}\ket{1}_3\\ \ket{\frac{3}{2},-\frac{1}{2}}_{1,2,3}&=\frac{1}{\sqrt{3}}\ket{1,-1}_{1,2}\ket{0}_3 + \sqrt{\frac{2}{3}}\ket{1,0}_{1,2}\ket{1}_3\\ \ket{\frac{3}{2},-\frac{3}{2}}_{1,2,3}&=\ket{1,-1}_{1,2}\ket{1}_3 \end{align} \(l=1/2\)のもの： \begin{align} \ket{\frac{1}{2},\frac{1}{2}}_{1,2,3}&=\frac{1}{\sqrt{3}}\ket{1,0}_{1,2}\ket{0}_3 - \sqrt{\frac{2}{3}}\ket{1,1}_{1,2}\ket{1}_3\\ \ket{\frac{1}{2},-\frac{1}{2}}_{1,2,3}&=\sqrt{\frac{2}{3}}\ket{1,-1}_{1,2}\ket{0}_3 - \frac{1}{\sqrt{3}}\ket{1,0}\ket{1}_3 \end{align}
これで一応全角運動量演算子\(\b{S}\)の \(\ket{l,m}\) 状態を求めることはできた。しかし\(\ket{\frac{1}{2},\frac{1}{2}}_{1,2,3}, \ket{\frac{1}{2},-\frac{1}{2}}_{1,2,3}\)の状態がそれぞれ2つずつあることには注意しなければいけない。2スピンのときは異なる\((l,m)\)の組によって、異なる状態が1つに指定されていたが、3スピンの場合には、\((l,m)\)だけではある状態を一意に指定できないのだ。だから本当は、上のように \(\ket{\frac{1}{2},\frac{1}{2}}_{1,2,3}, \ket{\frac{1}{2},-\frac{1}{2}}_{1,2,3}\) を一つの状態と \(=\) で結んでしまうのはまずい。

しかしながら、今回は1番目のスピンと2番目のスピンが 1 となっている状態や、0 となっている状態に、3番目のスピンをくっつけて3スピンの\(\ket{l,m}\)状態を構成するという方法をとったので、1,2 番目のスピンの合成角運動量の大きさ\(S_{12}^2\)の固有値\(l_{12}(l_{12}+1)\)をラベルとすれば、とりあえずはこれらの状態を区別することができる。

ということで、これらの式にさきほど求めた\(\ket{l,m}_{1,2}\)を代入して、\(l_{12}\)というラベルも足して、3スピンの場合をまとめよう。

1,2番目のスピンを合成してから、3番目のスピンをくっつけるというやり方を取ったことで、本来\((l,m)\)というラベルでは縮退してしまっていた状態を、\(S_{12}^2\)という演算子の固有値によって自然に分類できていたわけである。その方法以外にも、もちろん、2,3番目のスピンを合成してから1番目を付け足すということもできるはずで、そのときは\(S_{23}^2\)という演算子の固有値を使うことに対応する。しかしこのようなやり方だと、3つのスピンが等価に扱われて無くて少し気持ち悪い感じがする。等価にするには、3つのスピンを等価に扱うようなうまい演算子を持ってきて、それの固有値でラベル付けすれば良いはずだが、どんな演算子がいいのだろう？

---

6. Nスピンの場合

4スピンの場合の導出と式も書こうと思ったが、長くなりすぎるのと、めんどくさいのとでやめた。2スピン状態から、3スピン状態を作り出したのと同じ手続きを踏めば4スピン状態も構成できる。少しだけ具体的な話をすると、3スピン状態で\(l=3/2\)であった状態は、もう一つのスピンを足すと\(l=2\)の状態と\(l=1\)の状態に分離し、\(l=1/2\)であった状態は\(l=1\)の状態と\(l=0\)の状態に分離する。このページで紹介した1スピン～4スピンまでの\(\ket{l,m}\)状態の構成手続きは以下のような図として表すとわかりやすいかもしれない。

3スピン状態が\((l,m)\)だけでは一意に指定できなかったのだから、当然4スピン状態も\((l,m)\)だけでは一意に指定できない。しかしながら、上で小さく書いたようなことを考えると、同じ手続きで4スピン状態を構成した場合、\(\b{S}_{12}^2\)と\(\b{S}_{123}^2\)の固有値でラベル付けされた状態が自然に現れるわけだ。

Nスピン状態も同じように構成できるのだが、この言葉だけで終わるのも味気ない。そこで、その様子を簡潔に表す branching diagram と呼ばれる図を以下に紹介して終わりにしよう。基本的には上の図と同じことを表していて、丸の中の数字はその状態に何重の縮退があるかを示している。縮絨度がパスカルの三角形みたいになってて面白い。