静電ポテンシャルの多重極展開 - 球面調和関数
1.ルジャンドル多項式による多重極展開
前回みたように、任意の局在した電荷分布\(\rho(\b{r})\)がつくる静電ポテンシャルは、ルジャンドル多項式\(P_n(x)\)によって多重極展開
することができる。今回考える状況は下の図のような状況だ。多重極展開の形は、 \begin{align} \phi(\b{r}) &= \sum_{n=0}^\infty \phi_n(\b{r})\\ &=\frac{1}{4\pi\epsilon_0}\sum_{n=0}^{\infty}\frac{1}{r^{n+1}}\int d\b{r}'\rho(\b{r}')P_n(\cos\gamma)r'^n\tag{1} \end{align} のような感じだった。今回はルジャンドル多項式と球面調和関数の関係を使ってこの式を書き換え、より使いやすい形にすることを目標にする。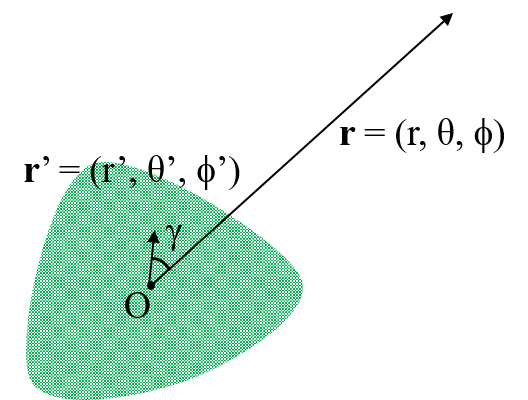
2.球面調和関数の加法公式
球面調和関数\(Y_l^m(\theta,\phi)\)
には、加法公式
と呼ばれる公式がある。それを以下に示す。証明はめんどくさそうなので、やる気が出れば調べてみようと思うが、今のところなんでこうなるのかはよく知らない。 \[P_l(\cos\gamma)=\frac{4\pi}{2l+1}\sum_{m=-l}^{l}{Y_l^m}^*(\theta',\phi')Y_l^m(\theta,\phi)\tag{2}\]3.球面調和関数による多重極展開
(2)の公式を(1)へ代入すると、 \begin{align} \phi(\b{r})&=\frac{1}{4\pi\epsilon_0}\sum_{l=0}^{\infty}\frac{1}{r^{l+1}}\int d\b{r}'\rho(\b{r}')\left[\frac{4\pi}{2l+1}\sum_{m=-l}^{l}{Y_l^m}^*(\theta',\phi')Y_l^m(\theta,\phi)\right]r'^l \\ &=\frac{1}{4\pi\epsilon_0}\sum_{l=0}^{\infty}\frac{1}{r^{l+1}}\left[\frac{4\pi}{2l+1}\sum_{m=-l}^{l}Y_l^m(\theta,\phi)\int d\b{r}'\rho(\b{r}'){Y_l^m}^*(\theta',\phi')r'^l\right]\tag{3} \end{align} となる。今回のテーマは(3)を出すことだったのだけど、(2)の公式を認めてしまったらあっさり出てしまった。係数\(4\pi/(2l+1)\)を半分に分けて、 \[F_l^m (\theta,\phi)=\sqrt{\frac{4\pi}{2l+1}}Y_l^m(\theta,\phi)\tag{4}\] を定義すればもう少しきれいに書ける。やってやると、 \[\phi(\b{r})=\frac{1}{4\pi\epsilon_0}\sum_{l=0}^{\infty}\frac{1}{r^{l+1}}\left[\sum_{m=-l}^{l}F_l^m(\theta,\phi)\int d\b{r}'\rho(\b{r}'){F_l^m}^*(\theta',\phi')r'^l\right]\tag{5}\] となる。
球面調和関数による展開では、ルジャンドル多項式のときのように、次数が上がるにつれて多極子モーメントを表すテンソルの次数が上がっていく、というようなことは起こらない。(定義の問題かも知れないが。) 球面調和関数によって上の(5)のように展開されたポテンシャルから、このときの電気多極子モーメント\(Q_{lm}\)は以下のように定義される。 \[Q_{lm}=\int d\b{r}'\rho(\b{r}'){F_l^m}^*(\theta',\phi')r'^l\tag{6}\] \(l=0\)のときが単極子、\(l=1\)のときが双極子、\(l=2\)のときが四極子に相当する。この\(Q_{lm}\)を使うとポテンシャルは \[\phi(\b{r})=\frac{1}{4\pi\epsilon_0}\sum_{l=0}^{\infty}\frac{1}{r^{l+1}}\left[\sum_{m=-l}^{l} Q_{lm}F_l^m(\theta,\phi)\right]\tag{7}\] となる。
この式を物理的に解釈すると結構面白い結果なのだ。
まず、\(Q_{lm}\)というのは、角度方向について球面調和関数\({Y_l^m}^*(\theta,\phi)\)をかけて積分することによって求められている。したがって、\(Q_{lm}\)というのは電荷分布を球面調和関数によって展開したときの展開係数である、といえるだろう。だから電荷分布が球面調和関数の一つによって表されている場合には、当然\(Q_{lm}\)はその一つの成分でのみ値を持ち、それ以外では0になる。
そこで(7)式を見てみると、ひとつの\(Q_{lm}\)だけが存在していたとしたら、静電ポテンシャルは\(Y_l^m(\theta,\phi)\)によって表されることになることがわかる。つまり、ある球面調和関数によって表される電荷分布からは、その球面調和関数によって表される静電ポテンシャルが作られるということだ。
これは、電位に関するポアソン方程式 \[\Delta \phi = -\frac{\rho(\b{r})}{\epsilon_0}\] の固有関数 (の角度成分) が球面調和関数であることに由来している。
しかも、この球面調和関数による展開方法は、量子力学における電子軌道が球面調和関数になることと非常に相性がよいという特徴がある。
ルジャンドル多項式による展開(1)よりも球面調和関数による展開(5)のほうが複雑に見えてしまうが、応用を考えるときには(5)というのはとても使いやすい式なのだ。