偏光による反射率・透過率とフレネルの式の導出
1.s,p偏光の境界条件
今回は反射率・透過率を求めるのだが、偏光によって境界条件の形が異なるのでそれぞれについて別々に考えないといけない。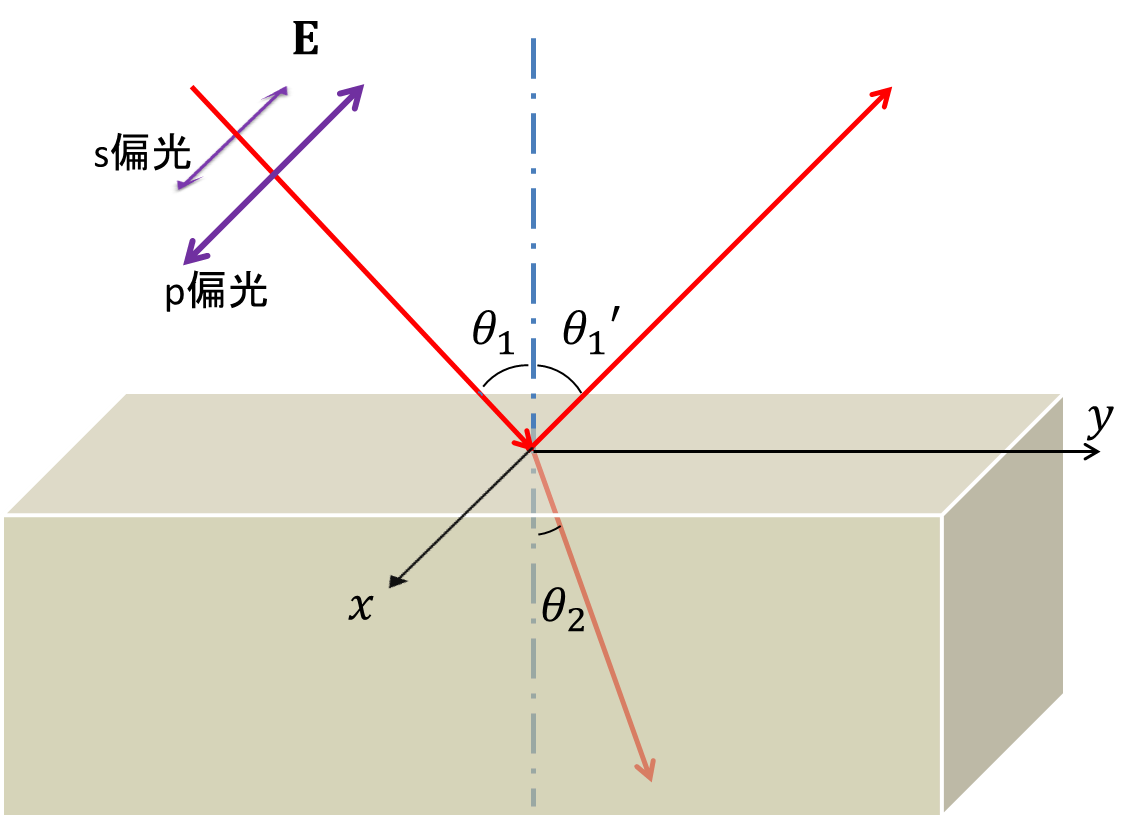
原点での境界条件の式は、s偏光について、 \begin{align} H_{1s}\cos\theta_1-H_{1s}'\cos\theta_1&=H_{2s}\cos\theta_2~~~(境界で磁界の平行成分が連続)\tag{1}\\ H_{1s}\sin\theta_1+H_{1s}'\sin\theta_1&=H_{2s}\sin\theta_2~~~(境界で磁束密度の垂直成分が連続)\tag{2} \end{align} これを電界の振幅\(E\)をつかって書き換えておくと、\(H=\frac{n}{\mu_0c}E\)なので、 \begin{align} \bar{n}_1E_{1s}\cos\theta_1-\bar{n}_1E_{1s}'\cos\theta_1&=\bar{n}_2E_{2s}\cos\theta_2\tag{1}\\ \bar{n}_1E_{1s}\sin\theta_1+\bar{n}_1E_{1s}'\sin\theta_1&=\bar{n}_2E_{2s}\sin\theta_2\tag{2} \end{align} さらにp偏光については、 \begin{align} E_{1s}\cos\theta_1-E_{1s}'\cos\theta_1&=E_{2s}\cos\theta_2~~~(境界で電界の平行成分が連続)\tag{3}\\ \bar{n}_1^2E_{1s}\sin\theta_1+\bar{n}_1^2E_{1s}'\sin\theta_1&=\bar{n}_2^2E_{2s}\sin\theta_2~~~(境界で電束密度の垂直成分が連続)\tag{4} \end{align} (1)から(4)式を入射光の振幅\(E_{1s}, H_{1s}\)で割ると、反射率と透過率の式に直すことができる。s,p偏光の電界振幅に関する反射率・透過率を\(r_{s,p}, t_{s,p}\)とすると、 \[\left\{\begin{align} 1-r_s&=t_s\frac{\bar{n}_2}{\bar{n}_1}\frac{\cos\theta_2}{\cos\theta_1} \tag{1'}\\ 1+r_s&=t_s\frac{\bar{n}_2}{\bar{n}_1}\frac{\sin\theta_2}{\sin\theta_1} \tag{2'} \end{align}\right.\] \[\left\{\begin{align} 1-r_p&=t_p\frac{\cos\theta_2}{\cos\theta_1} \tag{3'}\\ 1+r_p&=t_p\frac{\bar{n}_2^2}{\bar{n}_1^2}\frac{\sin\theta_2}{\sin\theta_1} \tag{4'} \end{align}\right. \] という式が得られる。
2.計算
あとはこの連立方程式を解くだけだ。\(\bar{n}_1\sin\theta_1 = \bar{n}_2\sin\theta_2\)という屈折の法則も使う必要はあるが。まあ適当に計算していこう。まずは(1')+(2'): \begin{align} 2&=t_s\frac{\bar{n}_2}{\bar{n}_1}\left(\frac{\bar{n}_1}{\bar{n}_2}+\frac{\cos\theta_2}{\cos\theta_1}\right)\\ 2\bar{n}_2\cos\theta_1&=t_s\frac{\bar{n}_2}{\bar{n}_1}\left(\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2\right)\\\\ t_s&=\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2} \end{align} これを(2')に代入して計算すれば、 \begin{align} 1+r_s&=\frac{\bar{n}_2}{\bar{n}_1}\frac{\sin\theta_2}{\sin\theta_1}\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2}\\ r_s&=\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2}-1\\\\ r_s&=\frac{\bar{n}_1\cos\theta_1-\bar{n}_2\cos\theta_2}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2} \end{align} となってs偏光に関してはできた。
さらにp偏光についてもやっていく。(3')+(4'): \begin{align} 2&=t_p\left(\frac{\cos\theta_2}{\cos\theta_1}+\frac{\bar{n}_2^2}{\bar{n}_1^2}\frac{\sin\theta_2}{\sin\theta_1}\right)\\ 2&=t_p\left(\frac{\cos\theta_2}{\cos\theta_1}+\frac{\bar{n}_2}{\bar{n}_1}\right)\\ 2\bar{n}_1\cos\theta_1&=t_p\left(\bar{n}_1\cos\theta_2+\bar{n}_2\cos\theta_1\right)\\\\ t_p&=\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_2+\bar{n}_2\cos\theta_1} \end{align} で、(3')に代入すれば、 \begin{align} 1-r_p&=\frac{\cos\theta_2}{\cos\theta_1}\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_2+\bar{n}_2\cos\theta_1}\\ r_p&=1-\frac{2\bar{n}_1\cos\theta_2}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2}\\\\ r_p&=\frac{\bar{n}_2\cos\theta_1-\bar{n}_1\cos\theta_2}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2} \end{align} これで全部出揃った。まとめると、 \begin{align} t_s&=\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2} \\ r_s&=\frac{\bar{n}_1\cos\theta_1-\bar{n}_2\cos\theta_2}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2}\\ t_p&=\frac{2\bar{n}_1\cos\theta_1}{\bar{n}_1\cos\theta_2+\bar{n}_2\cos\theta_1}\\ r_p&=\frac{\bar{n}_2\cos\theta_1-\bar{n}_1\cos\theta_2}{\bar{n}_1\cos\theta_1+\bar{n}_2\cos\theta_2} \end{align}\tag{5} となる。結構綺麗にまとまるのできもちいい。これが
フレネルの式
である。3.エネルギー反射率・透過率
(5)式によって、電界の振幅に関する反射率・透過率は分かったが、電磁波のエネルギーがどのくらい反射されているかについてはまだ計算しないといけない。4.Brewster角
(5)をみると、反射率\(r_s,r_p\)は0になることがあり得るのではないかと思える。これを調べてみよう。\(\cos\theta_2\)は屈折の法則を使うと、\(\theta_1\)によって表せる。 \begin{align} \cos^2\theta_2&=1-sin^2\theta_2\\ &=1-\frac{\bar{n}_1}{\bar{n}_2}\sin^2\theta_1\\ &=1-\left(\frac{\bar{n}_1}{\bar{n}_2}\right)^2(1-\cos^2\theta_1)\\ &=1-\left(\frac{\bar{n}_1}{\bar{n}_2}\right)^2+\left(\frac{\bar{n}_1}{\bar{n}_2}\right)^2\cos^2\theta_1\\ \cos\theta_2&=\sqrt{1-\left(\frac{\bar{n}_1}{\bar{n}_2}\right)^2+\left(\frac{\bar{n}_1}{\bar{n}_2}\right)^2\cos^2\theta_1} \end{align} ここからは話を簡単にするために、屈折率は実数だとしよう。