偏光と境界条件・反射・屈折の法則
1.偏光とその種類
光には、偏光
という概念が存在する。この概念は、特に光がある物質からある物質へと入射するときに重要となる。今回紹介するのはs偏光
とp偏光
の二つだ。この二つの偏光は電界の振動方向によって区別されるのだが、こういうのを言葉で説明しても意味がないので図で説明しよう。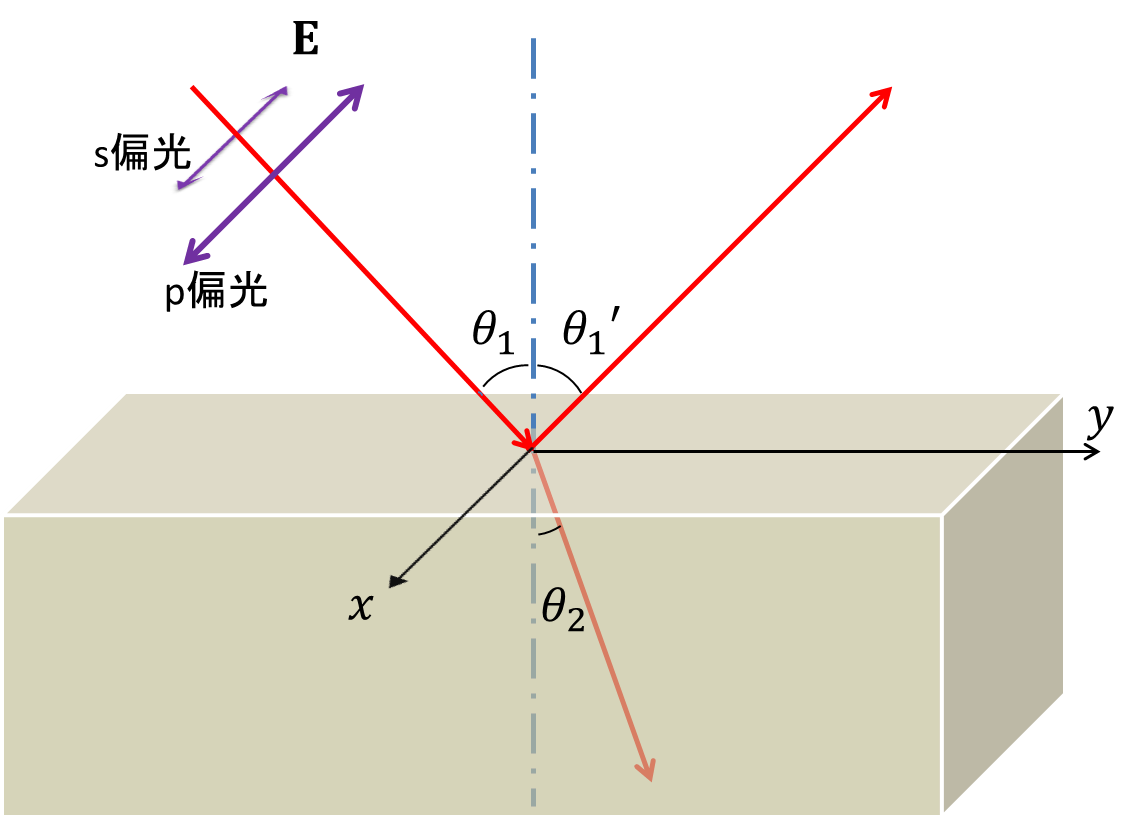
入射光や反射光が全て乗っている面のことを
入射面
と呼ぶのだが、(今回の場合はx=0の面)その言葉をつかって書けば、電界の振動方向が、s偏光では入射面に垂直、p偏光では入射面に平行、ということができる。ちなみにsというのはドイツ語で垂直という意味のsenkrecht, pというのは平行という意味でparallelということらしい。ちなみに、偏光の名前の付け方はその分野によってことなる。光学では上のように呼ぶのだが、電気工学では、s波をTE波(Transverse Electric Wave), p波をTM波(Transverse Magnetic Wave)と呼ぶらしい。もともと光が電磁波であると分かったのが、二つの分野が分離したあとだったからこんなようなややこしいことになるのだろう。しっかしなんとか統一してほしいものだ。これに限らず分野によって同じ現象を呼ぶのに違う名前を使うのはどんなに考えたって不便なのだから。
2.Maxwell方程式による境界条件
これからは屈折や反射という現象について扱って行きたいのだが、それをやるにはまず、異なる媒質の境目ではどのような現象が起きるのか、ということについてMaxwell方程式を用いて解析していかなければいけない。Maxwell方程式の積分形から分かるのだが、媒質1と2があったとして、媒質1での電界磁界をそれぞれ\(\b{E}_1,\b{H}_1\)、媒質2での電界磁界を\(\b{E}_2,\b{H}_2\)としよう。するとそのそれぞれの境界面に平行な成分\(E_{1\parallel},H_{1\parallel},E_{2\parallel},H_{2\parallel}\)の間には、 \[\left\{ \begin{array} ~E_{1\parallel} = E_{2\parallel} \\ H_{1\parallel} = H_{2\parallel} \end{array} \right.\] の関係が成り立つ。つまりはその境界面に平行な成分同士が連続であることが境界条件となるということだ。
もうひとつ関係式がある。それは電束密度\(\b{D}\)、磁束密度\(\b{B}\)に対して成り立つ境界条件で、こいつらに関しては境界面において、境界面に垂直な成分同士が連続である。同様に記号を定義して式で表すなら、 \[\left\{ \begin{array} ~D_{1\perp} = D_{2\perp} \\ B_{1\perp} = B_{2\perp} \end{array} \right.\] ここからは実際に反射や屈折についてしっかりと式を追いながら解析していこう。
3.具体的な境界条件
さあ反射や屈折
についてについて考えていこう。ちなみに下の図でz方向は上方向である。
さて、図では入射光がx=0の平面にのってやってきているとする。したがって入射光の波数ベクトルのx成分は0であり、\(\b{k}_1 = (0,\beta_1,\gamma_1)\)のようになる。だからといって反射光の波数ベクトルのx成分が0になるといってしまうのはまだ早い。いまからそこも導き出していく。
まずは平面波解の形を書いておく。s偏光を考えるので電界はx方向成分しか持たない。したがって、 \[\b{E} = E_x \b{e}_x e^{i\omega\left(t-\frac{\bar{n}}{c}(\alpha x + \beta y + \gamma z)\right)}\] のように書くことができる。また、磁界については \[\b{H} = (H_y \b{e}_y+H_z \b{e}_z) e^{i\omega\left(t-\frac{\bar{n}}{c}(\alpha x + \beta y + \gamma z)\right)}\] の形となる。ここで今からやるのは境界面の様子を調べることであったことを思い出して、境界面はz=0の面であるから、それを代入してやる。 \[\b{E} = E_x \b{e}_x e^{i\omega\left(t-\frac{\bar{n}}{c}(\alpha x + \beta y)\right)}\] これで準備完了だ。じゃあ実際に電磁界の境界面に平行な成分が連続になるという境界条件を使ってみよう。すると、 \[E_{1x}e^{i\omega\left(t-\frac{\bar{n}_1}{c}\beta_1 y\right)} + E_{1x}'e^{i\omega\left(t-\frac{\bar{n}_1}{c}(\alpha_1' x + \beta_1' y)\right)} = E_{2x}e^{i\omega\left(t-\frac{\bar{n}_2}{c}(\alpha_2 x + \beta_2 y)\right)} \tag{1}\] という式が成り立つ。(z方向成分は境界面に平行でないので上の式には現れない。)
さあ上で出た(1)(2)の両式は、x,y,tの値にかかわらず、常に成り立っていないといけない。もし一瞬でも、一箇所でもずれていたらMaxwell方程式に合わなくなってしまうからだ。
4.反射の法則・屈折の法則
例えば、(2)式のtとyだけ0にしてみよう。すると、 \[E_{1x}+ E_{1x}'e^{-i\omega\frac{\bar{n}_1}{c}\alpha_1' x} = E_{2x}e^{-i\omega\frac{\bar{n}_2}{c}\alpha_2 x} \tag{5}\] のようになるわけだが、ここから何が言えるか考えよう。ためしに(3)を代入してみる。 \begin{align} &E_{1x}+ E_{1x}'e^{-i\omega\frac{\bar{n}_1}{c}\alpha_1' x} = (E_{1x} + E_{1x}')e^{-i\omega\frac{\bar{n}_2}{c}\alpha_2 x} \\\\ &E_{1x}\left(1-e^{-i\omega\frac{\bar{n}_2}{c}\alpha_2 x}\right) + E_{1x}'\left(e^{-i\omega\frac{\bar{n}_1}{c}\alpha_1' x}-e^{-i\omega\frac{\bar{n}_2}{c}\alpha_2 x}\right) = 0 \end{align} こういうふうになる。さて、この式が絶対に成り立つためには何が必要だろうか?\(E_{1x}\)というのは入射光であり、その大きさは自分たちで任意に変えられるわけだ。\(E_{1x}\)というのは反射光の電界強度だが、たぶん入射光が強くなれば強くなるし、これも任意だろう。じゃあ上の式の左辺が0になるためには?といえばそれらの係数を0にするほかない。したがって、 \[\alpha_1' = \alpha_2 = 0 \tag{6}\] がいえる。これは何を表しているのかというと、反射光も屈折光も入射面(x=0)内に存在するということだ。当然のことかもしれないが、Maxwell方程式だけを根拠にして導き出すことができたことには価値がある。つぎ。tだけ0にする。上の結果(6)ともあわせて、 \[E_{1x}e^{-i\omega\frac{\bar{n}_1}{c}\beta_1 y} + E_{1x}'e^{-i\omega\frac{\bar{n}_1}{c}\beta_1' y} = E_{2x}e^{-i\omega\frac{\bar{n}_2}{c}\beta_2 y} \tag{7}\] 上と同じような議論に持ち込んでやる。(3)式を代入すれば、 \begin{align} &E_{1x}e^{-i\omega\frac{\bar{n}_1}{c}\beta_1 y} + E_{1x}'e^{-i\omega\frac{\bar{n}_1}{c}\beta_1' y} = (E_{1x}+E_{1x}')e^{-i\omega\frac{\bar{n}_2}{c}\beta_2 y}\\\\ &E_{1x} \left(e^{-i\omega\frac{\bar{n}_1}{c}\beta_1 y} -e^{-i\omega\frac{\bar{n}_2}{c}\beta_2 y} \right) + E_{1x}'\left(e^{-i\omega\frac{\bar{n}_1}{c}\beta_1' y}-e^{-i\omega\frac{\bar{n}_2}{c}\beta_2 y}\right) = 0 \end{align} これなら、上と同じように進められる。つまり、電界の係数=0ということから、 \[\bar{n}_1\beta_1 = \bar{n}_1\beta_1' = \bar{n}_2\beta_2\tag{7}\] となるのだ。これの前の二つを取り出したもの \[\beta_1 = \beta_1'\tag{8}\] を
反射の法則
と呼ぶ。さらに最初のひとつと最後のをくっつけたもの、 \[\bar{n}_1\beta_1 = \bar{n}_2\beta_2\tag{9}\] を屈折の法則
と呼ぶ。 \(\beta\)というのはそれぞれの光のy方向の進行方向だった。x方向の成分である\(\alpha\)は0だから、\(\beta\)が決まってしまえば自動的に\(\gamma\)も決まる。そこで、(8),(9)式を図の\(\theta_1,\theta_1',\theta_2\)を使って書き換えてやると、 \begin{align} \theta_1&=\theta_1'\tag{10}\\ \bar{n}_1\sin\theta_1 &= \bar{n}_2\sin\theta_2\tag{11} \end{align} となる。この形を用いることが多いだろう。
(11)式に関する補足
よくよく考えて見れば(11)式はかなり不可解な式になっている。というのも、\(\bar{n}\)というのは複素屈折率
で、一般には\(\bar{n}=n+i\kappa\)のような複素数なのである。つまり、(11)式を成立させる\(\theta\)は、複素数の角度になってしまう。この複素数の角度というのををどう理解するべきか、最初かなり悩んだ。
しかし、結局自分の中では、\(\theta\)から物理的な角度というイメージを捨ててしまうことで一応解決した。
(11)式は純粋に数学によって出てきた式であり、減衰の効果が無視できるような場合についてのみ、「たまたま」、\(\theta\)が物理的な角度となっているのだ。こういう場合についてのみ、高校物理でやるような屈折に関する説明をすることができる。
最後に屈折光を具体的に計算する手順を示しておこう。屈折の法則(11)式から\(\sin\theta=\beta\)を求めた後に、\(\gamma^2=cos^2\theta=1-\sin^2\theta\)によって\(\gamma\)を求めて、 \[\b{E} = E_x \b{e}_x e^{i\omega\left(t-\frac{\bar{n}}{c}(\beta y + \gamma z)\right)}\] に代入することによって、屈折光の解を求めるという計算となる。途中で複素数のsinやcosが出てくるがそれを気にせず計算し続けるのだ。それが境界条件を満足するための解なのだからしょうがない。