PN接合 - バンド図・拡散電位・空乏層・接合容量
1. PN接合とは
PN接合とは、その名のとおり、p型半導体とn型半導体をくっつけたものである。このページではPN接合のバンド図を描き、拡散電位を求めたり、PN接合における理想的な電圧-電流特性を求めたりしてみる。
2. バンド図
統計力学から、系が熱平衡状態となったとき、化学ポテンシャル (=フェルミエネルギー) はいたるところ一定になる。そこで pn 接合のバンド図を書くときには、まず双方のフェルミエネルギーが一致するようにp型・n型のバンド図を並べて書き、伝導帯底・価電子帯頂上のエネルギー\(E_C, E_V\)をなめらかにつないでやれば良い。ちょうど下の図のような感じになる。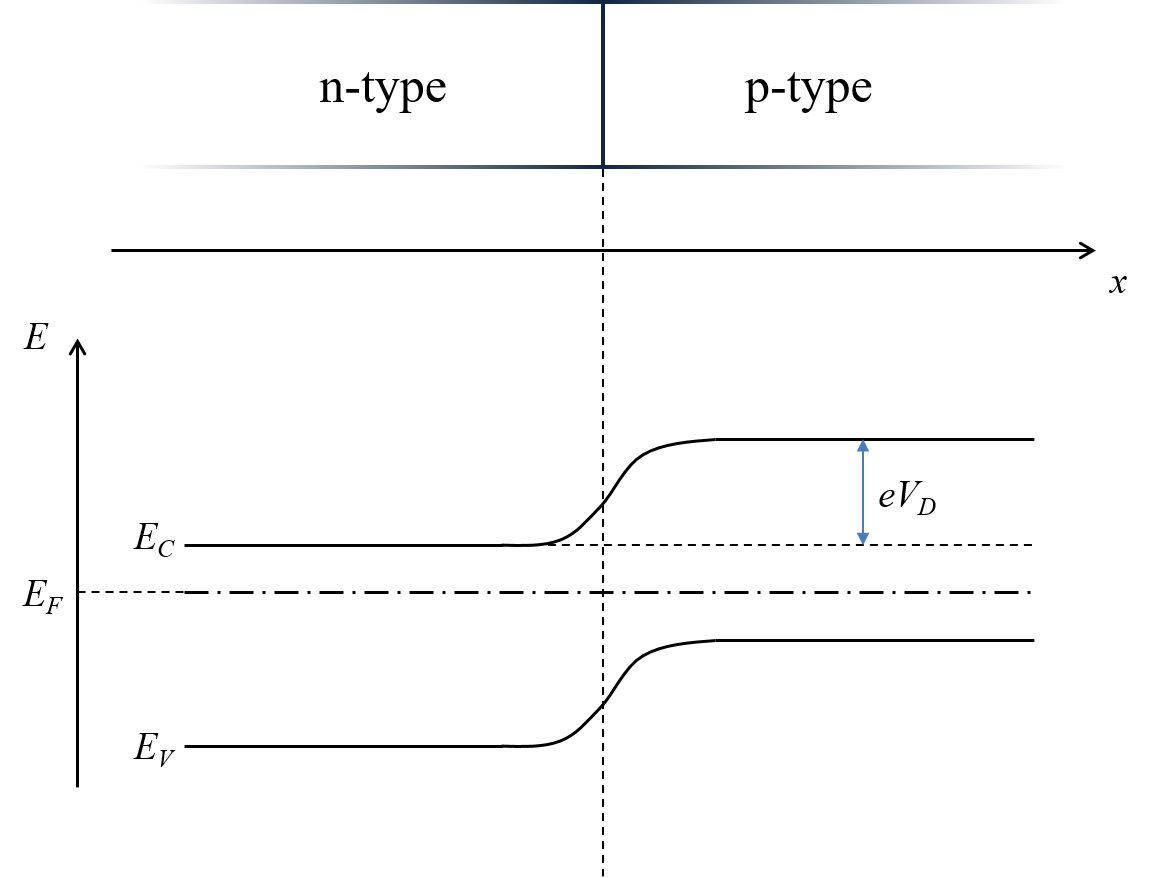
拡散電位
と呼び、\(V_D\)とかく。図では、エネルギーの単位にするために、電子の電荷\(e\)を掛けている。3. バンド図の曲がり方・空乏層
上で説明したバンド図の書き方はかなり適当なものだった。「なめらか」につなぐとはどういうことだろう。そこでここでは、バンドの曲がり方が具体的にどのような数式で表されるのか、導出してみよう。
導出には、ある仮定が必要である。それは、接合部周辺のある幅に渡って、キャリア (伝導帯電子・価電子帯正孔) の存在しない領域があるという仮定である。この領域を
空乏層
と呼ぶ。この仮定は物理的直感にも反さないだろう。p型領域には正孔がたくさん存在していて、逆にn型領域には電子がたくさん存在していることから、接合部では互いに消滅してしまうと考えられる。 以下の図のように空乏層が分布している状況を考えよう。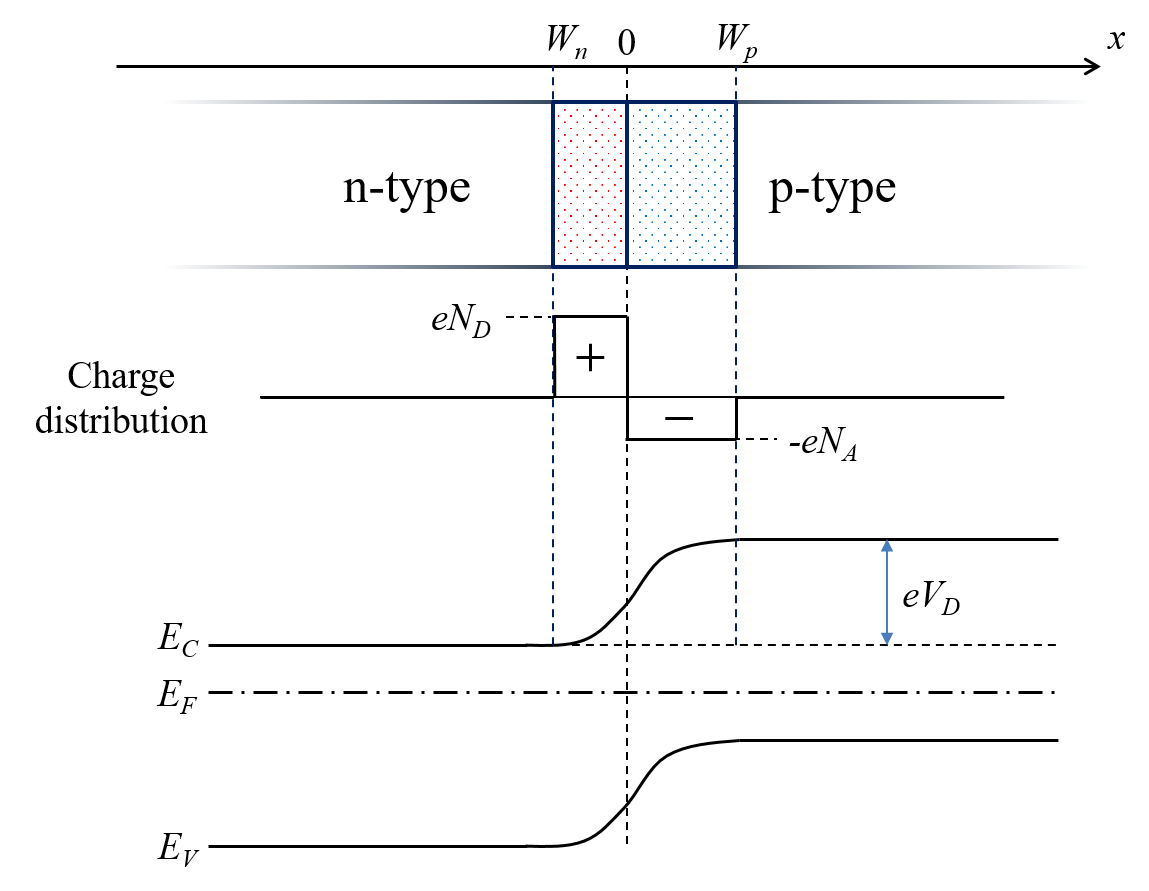
上の図のように電荷分布が階段状になるような接合を階段接合と呼ぶ。階段接合では、空乏層内でキャリアが全て消滅していると考えるが、もちろんこれは簡単化したモデルであり、現実にはもっといろいろな電荷分布がありうる。
さて、ここからエネルギーバンドの曲がり方を考えてみよう。電荷分布があるということは、そこには電場が存在していて、キャリアの感じる電位 (ポテンシャルエネルギー) の変化があるはずである。エネルギーバンド図は、基本的に電子の持っているエネルギーを描いたものだったから、この電位の変化がバンド図の「曲がり」に相当するものだろう。ということで、上の図のような電荷分布が作り出す電位 \(\phi(x)\) を位置 \(x\) の関数として求めてみよう。
一般に、電位 \(\phi(x)\) と電荷分布 \(\rho(x)\) には \[\frac{d^2\phi}{dx^2} = -\frac{\rho(x)}{\epsilon} \tag{2}\] という関係があるので、境界条件を適当にセットしてやって、この微分方程式を解けば良い。(\(\epsilon\)は誘電率。)
境界条件を設定しよう。まず、電位の基準点を\(x=-W_n\)に取ることにすると、 \[\phi(-W_n) = 0 \tag{3}\] である。また、拡散電位 \(V_D\) は図から \(V_D = E_{Cp} - E_{Cn}\) であり、これはn型・p型半導体のフェルミ準位の位置、すなわちそれぞれの不純物濃度のみで決定される定数である。そこでこれを境界条件として使うことができて、 \[\phi(W_p) = -V_D \tag{4}\] とする。図は電子のエネルギーを描いているものなので、電位に換算すると正負が反転することに注意しよう。
この問題を解くときに勘違いしてはいけないのは、拡散電位 \(V_D\) は既知のものであり、この(3)式を満たすように \(W_n\) や \(W_p\) が決まるということだ。
さらにもうひとつ、次は電場 \(F(x)\) についての境界条件を設定する。キャリアが十分にいる領域は、空乏層と比較するとほとんど金属的に振る舞うだろうから、空乏層端において電場 \(F(x)\) が0、つまり \[F(-W_n) = F(W_p) = 0 \tag{5}\] という条件を設定しよう。ここまでやっておいて、微分方程式 (2) を解く。まず \(-W_n \leq x \leq 0\) の領域では、 \[\rho(x) = eN_D\] なので、 \[\frac{d^2\phi}{dx^2} = -\frac{eN_D}{\epsilon}\] 両辺を積分して \(F(-W_n) = -\left.\frac{d\phi}{dx}\right|_{x=-W_n} = 0\)の境界条件を使うと \[\frac{d\phi}{dx} = -\frac{eN_D}{\epsilon}(x+W_n)\] を得る。さらに両辺をもう一度積分して、\(\phi(-W_n) = 0\)の条件から \[\phi(x) = -\frac{eN_D}{2\epsilon}(x+W_n)^2\] を得る。これが\(-W_n \leq x \leq 0\) の領域における解である。
次にもう一方 \(0 \leq x \leq W_p\) も解いてやろう。この領域では \[\rho(x) = -eN_A\] なので \[\frac{d^2\phi}{dx^2} = \frac{eN_A}{\epsilon}\] 積分して \(F(W_p) = 0\) の境界条件から \[\frac{d\phi}{dx} = \frac{eN_A}{\epsilon}(x-W_p)\] を得る。さらに積分して、\(\phi(W_p) = -V_D\) から、 \[\phi(x) = \frac{eN_A}{2\epsilon}(x-W_p)^2 - V_D\] である。
さて、これで微分方程式自体は解けた。まとめると \[\phi(x) = \left\{\begin{array}{cc} -\frac{eN_D}{2\epsilon}(x+W_n)^2 & (-W_n \leq x \leq 0)\\ \frac{eN_A}{2\epsilon}(x-W_p)^2 - V_D & (0 \leq x \leq W_p) \end{array}\right.\tag{6}\] である。
4. 空乏層幅
ここまでで、接合部に生じる空乏層幅が \(W_n, W_p\) であると仮定して、接合部の電位分布を求めることができた。しかし先にも述べたように、空乏層幅 \(W_n, W_p\) は、空乏層両端の電位差が拡散電位 \(V_D\) と等しくなるように決まる。そこでここでは 上で求めた電位分布 (6) が\(x = 0\)で連続であるという条件と、電荷量に関する条件 \(N_D W_n = N_A W_p\) から \(W_n, W_p\)を求める。
電位分布が\(x = 0\)で連続であるためには、 \[-\frac{eN_D}{2\epsilon}W_n^2 = \frac{eN_A}{2\epsilon}W_p^2 - V_D \tag{7}\] が成り立つ必要がある。この式に \(W_n = \frac{N_A}{N_D} W_p\) を代入してやると \begin{align} -\frac{e}{2\epsilon}\frac{N_A^2}{N_D}W_p^2 &= \frac{eN_A}{2\epsilon}W_p^2 - V_D \\ \frac{eN_A}{2\epsilon}\left(1+\frac{N_A}{N_D}\right)W_p^2 &= V_D \\ W_p &= \sqrt{\frac{2\epsilon}{eN_A}\frac{1}{1+\frac{N_A}{N_D}}V_D} \end{align} と\(W_p\)が求められる。全く同様に \(W_n\) も計算できて、 \[W_n = \sqrt{\frac{2\epsilon}{eN_D}\frac{1}{1+\frac{N_D}{N_A}}V_D}\] を得る。
5. バイアス電圧
pn 接合を実際に使うときには、当然何らかの電圧をかけて使用する。直流のバイアス電圧 \(V\) をかけたときには、もはや系は熱平衡状態にあるとはいえない。バンド図は拡散電位 \(V_D\) に加えて、バイアス電圧 \(V\) の分だけエネルギーバンド \(E_C, E_V\) がずれたような形となり、以下のようになる。\(V\) は順方向バイアス (エネルギー障壁が小さくなる方向) を正としている。
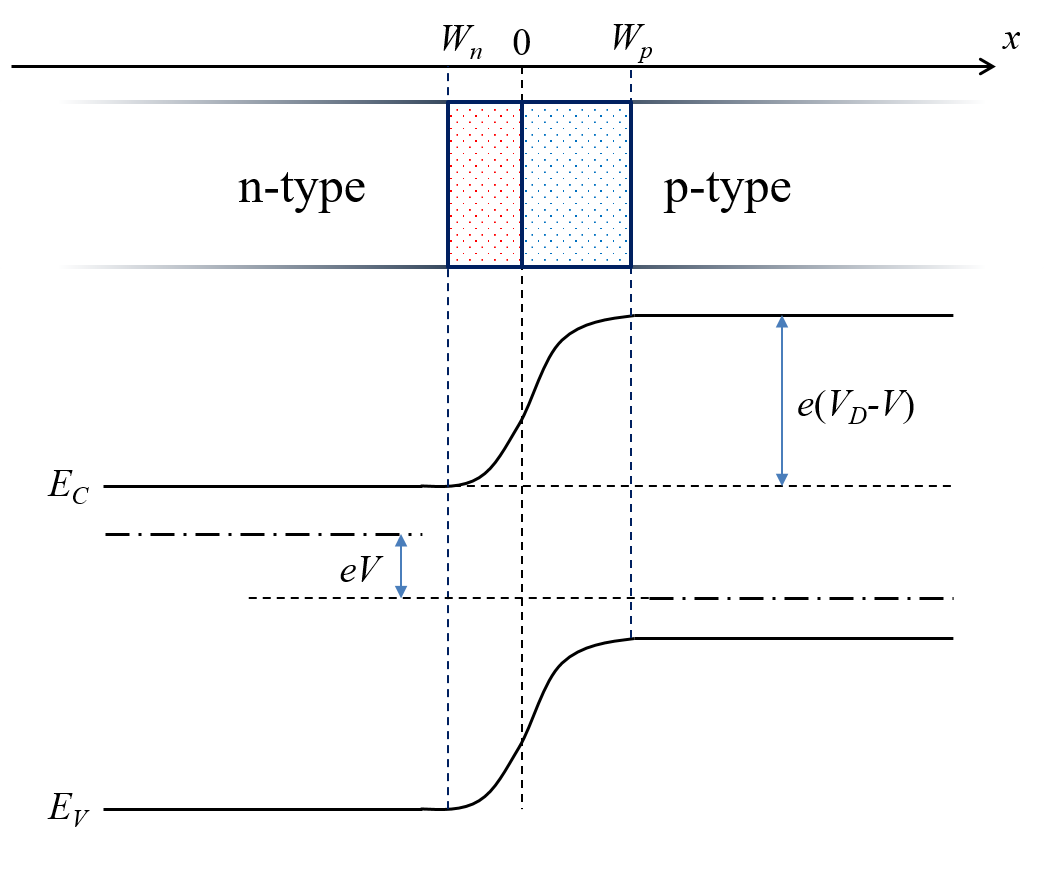
図からもわかるように、バイアス電圧が加わっても、基本的に解く問題は同じである。ただ単にこれまでの議論の \(V_D\) を \(V_D - V\) に置き換えてやれば良い。したがって、例えばこの場合の空乏層幅は、 \begin{align} W_n &= \sqrt{\frac{2\epsilon}{eN_D}\frac{1}{1+\frac{N_D}{N_A}}(V_D-V)} \\ W_p &= \sqrt{\frac{2\epsilon}{eN_A}\frac{1}{1+\frac{N_A}{N_D}}(V_D-V)} \end{align} となる。
6. 接合容量
最後に空乏層幅や拡散電位を実験的に求めるために測定される接合容量
について書いて、今回は終わりとしよう。空乏層ではキャリアが存在しておらず、電気抵抗が他の部分と比べて非常に高くなっている。そこで空乏層は近似的に、平行平板電極に挟まれた絶縁体とみなすことができるだろう。電磁気学の練習問題でやるように、厚み \(d\), 誘電率 \(\epsilon\) の誘電体が平行平板電極に挟まれているとき、単位面積あたりのキャパシタンス \(C\) は \[C = \frac{\epsilon}{d}\] である。したがって、空乏層がもつキャパシタンスは、\(d = W_n + W_p\) として、 \[C = \frac{\epsilon}{\sqrt{\frac{2\epsilon}{eN_A}\left(\frac{1}{N_A} + \frac{1}{N_D}\right)(V_D-V)}}\] となる。両辺を 2 乗して逆数を取れば、 \[\frac{1}{C^2} = \frac{2}{\epsilon eN_A}\left(\frac{1}{N_A} + \frac{1}{N_D}\right)(V_D-V)\] である。この式から、(階段接合の場合) バイアス電圧 \(V\) を変えながら \(1/C^2\) を測定してプロットしていけば、その傾きと切片から拡散電位と空乏層幅が求められるのだ。