Swap test と quantum neuron について

1. やること

今回は、swap test と呼ばれている量子アルゴリズムについて紹介します。swap test とは、適当な2つの状態\(\ket{\psi}\), \(\ket{\phi}\)の内積の大きさ\(|\braket{\phi}{\psi}|^2\)を、1つの補助qubitを使いながら上手く評価するアルゴリズムです。とても短い量子回路なので、アルゴリズムという呼び方が適切かどうかはわかりません。Quantum Fingerprinting というアルゴリズムのサブルーチンとして現れましたが、とても使い勝手が良いので色んな所で使われています。

Swap test だけだとさすがに短くなりすぎるので、少し一般化したものもついでに書きます。

4以降の一般化の方は僕の趣味の計算です。でもquantum neuronを見に来た人は見てね。

2. Swap ゲート

Swap test では、その名前から予想がつくように、swap ゲートを使います。このページを見ている人なら、きっと Swap ゲートは知っているとは思いますが、一応知らない人も読めるように、ということで swap ゲートの紹介から始めます。

Swap ゲートとは、読んで字の如く、量子状態を「交換」するゲートのことです。なんでこんな記号なのか知りませんが、量子回路の記号は下図を使います。

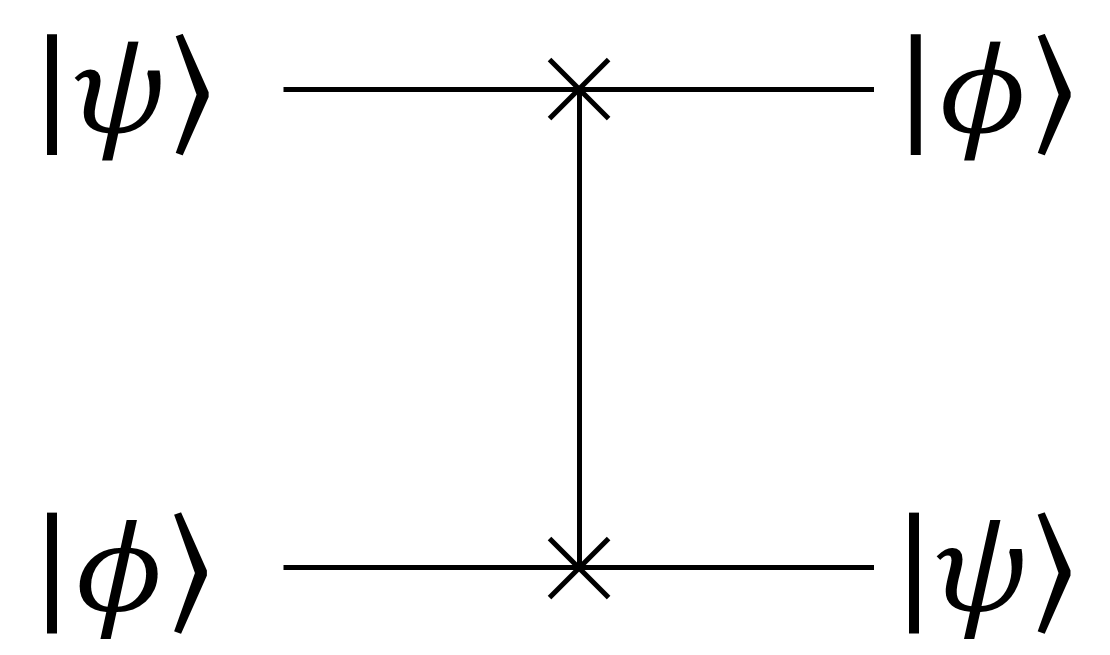
式で書くなら、 \[\ket{\psi}_1\ket{\phi}_2 \xrightarrow{\text{SWAP}}\ket{\phi}_1\ket{\psi}_2\] です。量子状態を交換するだけなので簡単ですね。さっそくswap testの説明に入りましょう。

3. Swap test

本題です。Swap test は次のような量子回路を使います。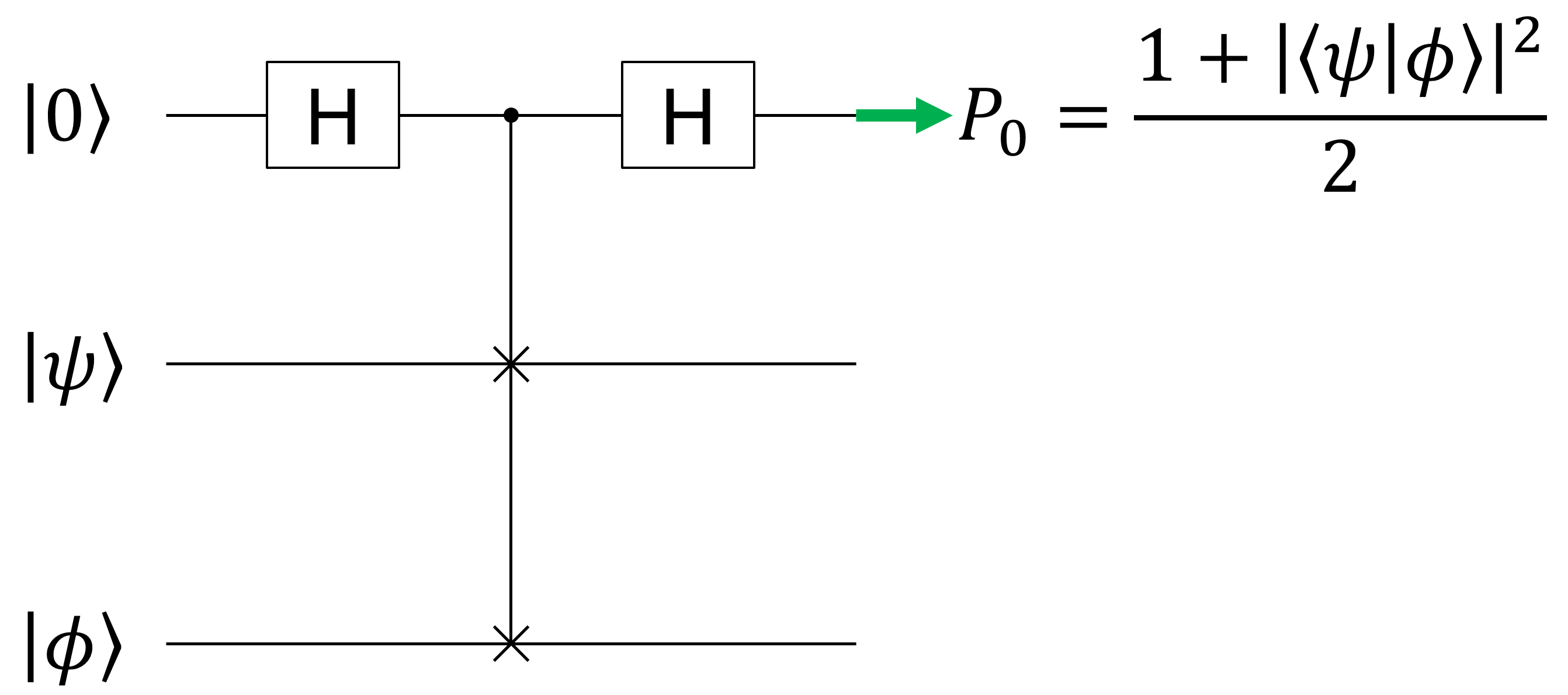

一つずつ追っていきましょう。便宜上、上のqubitから 0, 1, 2 の番号をつけることにします。まず最初の H: アダマールゲートによって、 \begin{align} \ket{0}_0\ket{\psi}_1\ket{\phi}_2 &\to \frac{1}{\sqrt{2}}(\ket{0}_0+\ket{1}_0)\ket{\psi}_1\ket{\phi}_2 \\ &\to \frac{1}{\sqrt{2}}\ket{0}_0\ket{\psi}_1\ket{\phi}_2+\frac{1}{\sqrt{2}}\ket{1}_0\ket{\psi}_1\ket{\phi}_2 \end{align} となります。

次の回路記号は、swapゲートとはpとは少しだけ違いますね。swapゲートの上から線が伸びていて、0番目の qubit に黒丸でくっついています。これは、controlled swap ゲートで、0番目のqubitが\(\ket{1}\)の場合だけ、swapをかけるというものです。したがって、このゲートによって次の変化が起きます。 \begin{align} &\to \frac{1}{\sqrt{2}}\ket{0}_0\ket{\psi}_1\ket{\phi}_2+\frac{1}{\sqrt{2}}\ket{1}_0\ket{\phi}_1\ket{\psi}_2 \end{align} \(\ket{1}_0\)がついている第2項だけ、swapが起きるわけです。

さて、最後です。アダマールゲートによって、 \begin{align} &\to \frac{1}{2}(\ket{0}_0+\ket{1}_0)\ket{\psi}_1\ket{\phi}_2+\frac{1}{2}(\ket{0}_0-\ket{1}_0)\ket{\phi}_1\ket{\psi}_2\\ &\to \frac{1}{2}\ket{0}_0(\ket{\psi}_1\ket{\phi}_2+\ket{\phi}_1\ket{\psi}_2) + \frac{1}{2}\ket{1}_0(\ket{\psi}_1\ket{\phi}_2-\ket{\phi}_1\ket{\psi}_2)\\ &:= \ket{\Psi} \end{align} という状態が得られます。

ここで最後に0番目のqubitを観測して、\(\ket{0}_0\)を得る確率\(P_0\)を計算してみます。するとそこに、\(\ket{\psi}\)と\(\ket{\phi}\)の内積が現れるのです。一般に、量子状態\(\ket{\Psi}\)が与えられたとき、その状態を観測して\(\ket{\alpha}\)を得る確率は、 \[P_\alpha = |\braket{\alpha}{\Psi}|^2\] で与えられます。今計算するのは、「0番目のqubitが\(\ket{0}\)になる」という確率ですから、1番目と2番目のqubitがどうなっていても構いません。そこで、1番目と2番目のqubitの基底を\(\{\ket{n}\}=\{\ket{00},\ket{01},\ket{10},\ket{11}\}\)とすると、求める確率\(P_0\)は \[P_0 = \sum_n |(\bra{0}_0\bra{n}_{1,2})\ket{\Psi}|^2\] と書けます。これを計算すると、 \begin{align} P_0 &= \sum_n \left|\bra{0}_0\bra{n}_{1,2}\left[\frac{1}{2}\ket{0}_0(\ket{\psi}_1\ket{\phi}_2+\ket{\phi}_1\ket{\psi}_2) + \frac{1}{2}\ket{1}_0(\ket{\psi}_1\ket{\phi}_2-\ket{\phi}_1\ket{\psi}_2)\right]\right|^2\\ &= \frac{1}{4}\sum_n |\bra{n}_{1,2}(\ket{\psi}_1\ket{\phi}_2+\ket{\phi}_1\ket{\psi}_2)|^2\\ &= \frac{1}{4}\sum_n (\bra{\psi}_1\bra{\phi}_2+\bra{\phi}_1\bra{\psi}_2)\ket{n}_{1,2}\bra{n}_{1,2}(\ket{\psi}_1\ket{\phi}_2+\ket{\phi}_1\ket{\psi}_2)\\ &= \frac{1}{4}(\bra{\psi}_1\bra{\phi}_2+\bra{\phi}_1\bra{\psi}_2)\left(\sum_n \ket{n}_{1,2}\bra{n}_{1,2}\right)(\ket{\psi}_1\ket{\phi}_2+\ket{\phi}_1\ket{\psi}_2)\\ &= \frac{1}{4}(\bra{\psi}_1\bra{\phi}_2+\bra{\phi}_1\bra{\psi}_2)(\ket{\psi}_1\ket{\phi}_2+\ket{\phi}_1\ket{\psi}_2)\\ &= \frac{1}{4}(1+1+2\braket{\phi}{\psi}\braket{\psi}{\phi})\\ &= \frac{1+|\braket{\phi}{\psi}|^2}{2} \end{align} となり、確かに、0番目のqubitが\(\ket{0}\)と観測される確率が、\(\ket{\psi}\)と\(\ket{\phi}\)の内積に関係して決まることがわかりました。Swap test を使えば、適当な量子状態の間の内積を、それらの詳細情報を知らずとも測ることができるわけです。swap testを使わずに内積を測る方法を考えてみると、これが結構すごいことがわかります。使わずに内積を計算する方法として、例えば\(\ket{\psi}=\alpha_1\ket{0}+\beta_1\ket{1}\)と\(\ket{\phi}=\alpha_2\ket{0}+\beta_2\ket{1}\)の係数\(\alpha_1,\alpha_2,\beta_1,\beta_2\)を何回も観測して求めてから、\(\alpha_1^*\alpha_2+\beta_1^*\beta_2\)と内積を計算する方法を考えてみましょう。この場合、swap testでは1つの量\(P_0\)を求めるだけで良かったのに対して、係数\(\alpha_1,\alpha_2,\beta_1,\beta_2\)という4つの量を求めることになり、測定の量が4倍に増えてしまいます。1 qubitの状態間では4倍で済んでいますが、係数を求めてやる方法では、qubit数が増えれば指数関数的に時間がかかります。ということで、swap testは結構便利なのです。

だからといって、内積を求めたいときなんかあるのか？というのはごもっともな指摘です。でも、例えば最初にあげたQuantum Fingerprintingであったり、Quantum Support Vector Machine だったりというアルゴリズムでは、こういう内積を求めることが重要だったりします。

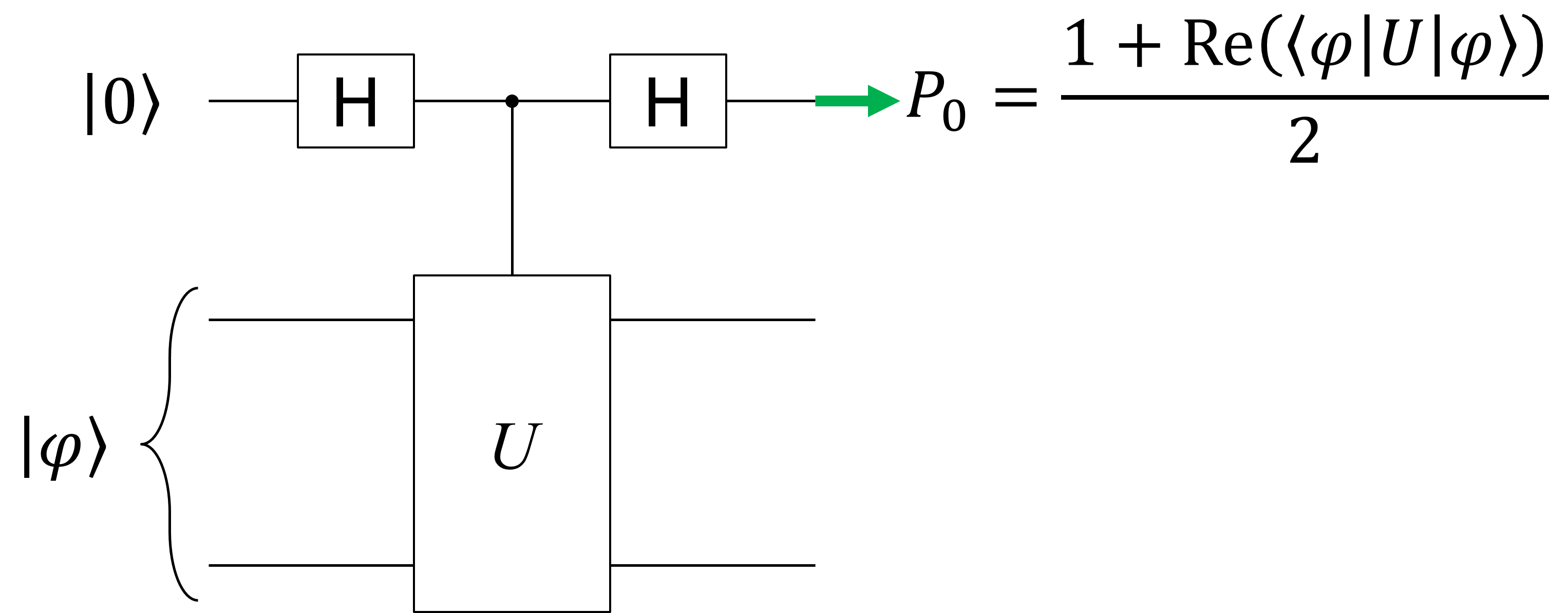
4. 一般化

次は一般化してみます。さっきまでswapだった部分を、任意のユニタリー演算子\(U\)に変えてみましょう。どうなるでしょうか？

計算してみましょう。さっきとほとんど同じ計算になるので、詳細は飛ばしますが、最後の状態は \begin{align} &\ket{0}_0\ket{\psi}_1\ket{\phi}_2\\ &\to \frac{1}{2}\ket{0}_0(\ket{\psi}_1\ket{\phi}_2+U\ket{\psi}_1\ket{\phi}_2) + \frac{1}{2}\ket{1}_0(\ket{\psi}_1\ket{\phi}_2-U\ket{\psi}_1\ket{\phi}_2) \end{align} となり、0番目のqubitが\(\ket{0}\)と観測される確率を計算してみると、 \begin{align} P_0 &= \frac{1}{4}(\bra{\psi}_1\bra{\phi}_2+\bra{\psi}_1\bra{\phi}_2U^\dagger)(\ket{\psi}_1\ket{\phi}_2+U\ket{\psi}_1\ket{\phi}_2)\\ &= \frac{1}{4}(1+1+\bra{\psi}_1\bra{\phi}_2U^\dagger\ket{\psi}_1\ket{\phi}_2 + \bra{\psi}_1\bra{\phi}_2 U\ket{\psi}_1\ket{\phi}_2)\\ &= \frac{1}{4}(2+(\bra{\psi}_1\bra{\phi}_2U\ket{\psi}_1\ket{\phi}_2)^* + \bra{\psi}_1\bra{\phi}_2 U\ket{\psi}_1\ket{\phi}_2)\\ &= \frac{1+\text{Re}\left(\bra{\psi}\bra{\phi} U\ket{\psi}\ket{\phi}\right)}{2} \end{align} となります。ここまで計算してみると、別に最初の状態が積状態\(\ket{\psi}_1\ket{\phi}_2\)である必要はなさそうなので、1番目のqubitと2番目のqubitの状態をあわせたものを\(\ket{\varphi}\)と置くと、 \[P_0 = \frac{1+\text{Re}\left(\bra{\varphi} U\ket{\varphi}\right)}{2}\] が得られることがわかります。

iterative phase estimationと同じ形ですね。swap test はiterative phase estimationの特別な場合と言っても良さそうです。

4. もう少し一般化

もう少し一般化します。0番目のqubitのアダマールゲートも、任意のゲート\(V\)に変えてみましょう。以下のような回路です。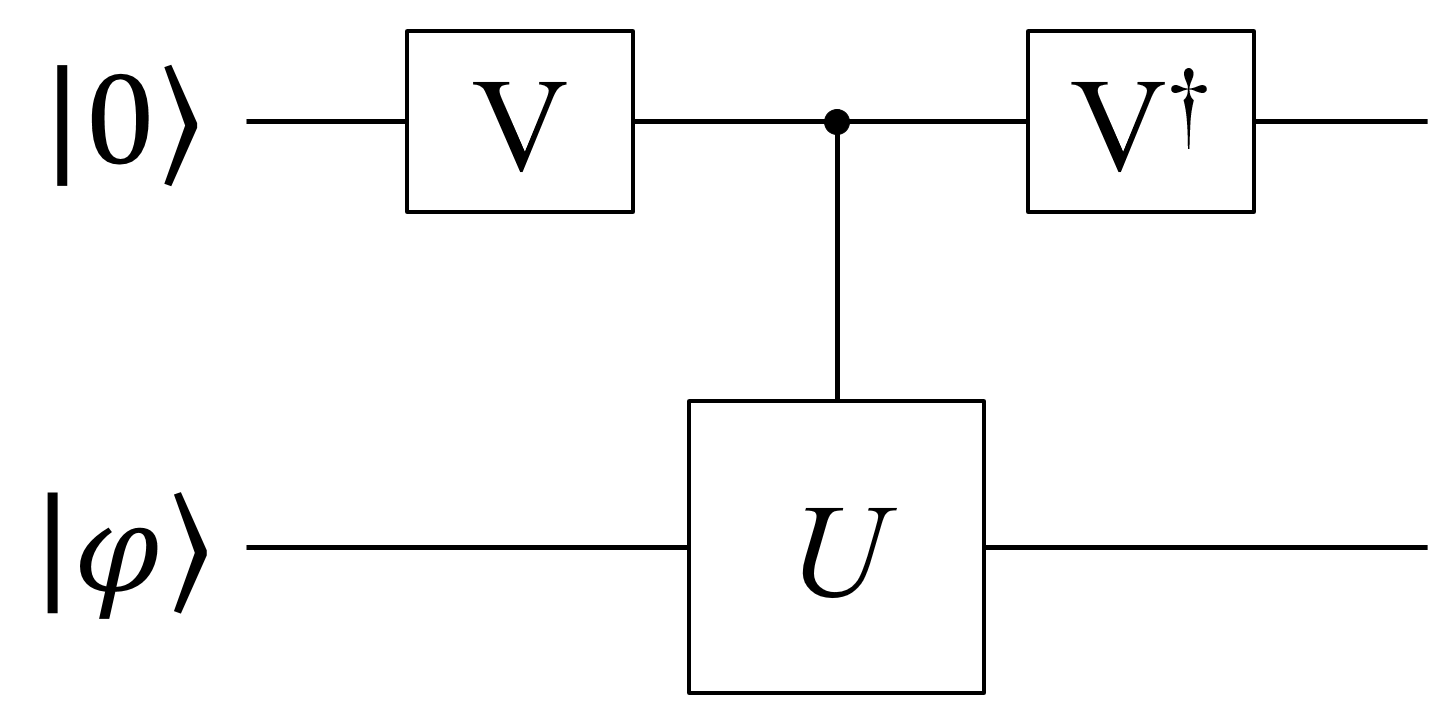

一般に、1qubit のユニタリー演算子は、\(|\alpha|^2+|\beta|^2 = 1\)となる２つの複素数\(\alpha,\beta\)を使って、 \[V = \left(\begin{array}{cc}\alpha&-\beta^*\\ \beta&\alpha^*\end{array}\right)\] と書けます。これを使って上の回路の出力を計算してみると、 \begin{align} &\ket{0}\ket{\varphi}\\ &\to (\alpha\ket{0}+\beta\ket{1})\ket{\varphi}\\ &\to \alpha\ket{0}\ket{\varphi}+\beta\ket{1}(U\ket{\varphi})\\ &\to \alpha(\alpha^*\ket{0}-\beta\ket{1})\ket{\varphi}+\beta(\beta^*\ket{0}+\alpha\ket{1})(U\ket{\varphi})\\ &\to \ket{0}\left(|\alpha|^2\ket{\varphi} + |\beta|^2U\ket{\varphi}\right) - \alpha\beta\ket{1}\left(\ket{\varphi}-U\ket{\varphi}\right) \end{align} となります。ここから、0番目のqubitが\(\ket{0}\)と観測される確率は \begin{align} P_0 &= \sum_n|\bra{n}\left(|\alpha|^2\ket{\varphi} + |\beta|^2 U\ket{\varphi}\right)|^2 \\ &= \left(|\alpha|^2\bra{\varphi} + |\beta|^2 \bra{\varphi}U^\dagger\right)\left(|\alpha|^2\ket{\varphi} + |\beta|^2 U\ket{\varphi}\right) \\ &= |\alpha|^4 + |\beta|^4 + |\alpha|^2|\beta|^2 \bra{\varphi}U^\dagger\ket{\varphi} + |\alpha|^2|\beta|^2 \bra{\varphi}U\ket{\varphi} \\ &= |\alpha|^4 + |\beta|^4 + |\alpha|^2|\beta|^2 (\bra{\varphi}U\ket{\varphi})^* + |\alpha|^2|\beta|^2 \bra{\varphi}U\ket{\varphi} \end{align} ということで、 \[P_0 = |\alpha|^4 + |\beta|^4 + 2|\alpha|^2|\beta|^2 \text{Re}(\bra{\varphi}U\ket{\varphi})\] あるいは、\(|\alpha|^2 + |\beta|^2 = 1\)を使うと \[P_0 = 1 - 2|\alpha|^2|\beta|^2 (1- \text{Re}(\bra{\varphi}U\ket{\varphi}))\] と求まります。

ここから、内積\(\bra{\varphi}U\ket{\varphi}\)を求めたい、という動機の下では、\(V\)としてアダマールゲートが最適であることがわかります。そのような動機では、結果に内積の影響を強く出すために、係数\(2|\alpha|^2|\beta|^2\)が大きいほうが良いです。その最大値は、受験でおなじみの相加相乗平均の不等式から求められます。具体的には、 \[|\alpha||\beta| \leq \frac{1}{2}(|\alpha|^2 + |\beta|^2) = \frac{1}{2}\] で、等号成立は\(|\alpha|=|\beta|\)のときだけなので、\(2|\alpha|^2|\beta|^2\)は、\(|\alpha|=|\beta|=1/\sqrt{2}\)のときに最大値\(1/2\)を取ります。アダマールゲートはまさにその条件を満たしていますね。

\(|\alpha|=|\beta|=1/\sqrt{2}\)でありさえすれば良い、ということは、最適は別にアダマールゲートに限りません。例えば\(V\)としてy軸回転\(R_y(\pi/2)\)を使っても良いことがわかります。

5. 測定後の状態

いちおう測定した後の状態も調べてみましょう。\(\ket{0}\)が出た時、測定後、もともと\(\ket{\varphi}\)が入っていたqubitの状態は \begin{align} \ket{\psi_0} = \frac{1}{\sqrt{P_0}}\left(|\alpha|^2\ket{\varphi} + |\beta|^2U\ket{\varphi}\right) \end{align} となり、一方で\(\ket{1}\)が出た時、 \begin{align} \ket{\psi_1} = -\frac{\alpha\beta}{\sqrt{P_1}}\left(\ket{\varphi} - U\ket{\varphi}\right) \end{align} ただし、\(P_1\)は\(\ket{1}\)が出る確率で、 \[P_1 = 2|\alpha|^2|\beta|^2(1- \text{Re}(\bra{\varphi}U\ket{\varphi}))\] です。

6. Quantum neuron

ここまで書いて、これってこの前出ていた Quantum neuron (arXiv) と (ほとんど) 同じだ！となったので紹介します。

ここでは、入力する状態を\(\ket{\varphi}=\ket{0}\)とします。

このとき、測定後の状態はそれぞれ \begin{align} \ket{\psi_0} &= \frac{1}{\sqrt{|\alpha|^4 + |\beta|^4 + 2|\alpha|^2|\beta|^2 \text{Re}(\bra{0}U\ket{0})}}\left(|\alpha|^2 + |\beta|^2U\right)\ket{0}\\ \ket{\psi_1} &= -\frac{\alpha\beta}{|\alpha||\beta|\sqrt{2(1- \text{Re}(\bra{0}U\ket{0}))}}\left(I - U\right)\ket{0} \end{align} と書けます。これらの状態は、\(\ket{0}\)に、それぞれ、 \begin{align} W_0 &= \frac{1}{\sqrt{|\alpha|^4 + |\beta|^4 + 2|\alpha|^2|\beta|^2 \text{Re}(\bra{0}U\ket{0})}}\left(|\alpha|^2 + |\beta|^2U\right)\\ W_1 &= -\frac{\alpha\beta}{|\alpha||\beta|\sqrt{2(1- \text{Re}(\bra{0}U\ket{0}))}}\left(I - U\right) \end{align} という変換をかけた状態になっています。ここまでは一般の状態\(\ket{\varphi}\)でも成り立つことですが、\(\ket{\varphi}=\ket{0}\)に制限したのには、\(\bra{\varphi}U\ket{\varphi}=0\)を成り立たせて、式を簡単にしてしまいたいという野望のためです。\(\bra{\varphi}U\ket{\varphi}=0\)を任意の状態\(\ket{\varphi}\)で成り立たせるような\(U\)は存在しないので、一つの状態に限定してしまうわけです。

\(\bra{0}U\ket{0}=0\)が成り立つような\(U\)というと、\(U\ket{0}=e^{i\alpha}\ket{1}\)となるようなものですから、例えば\(U=X\)や\(U=Y\)というゲートが考えられます。このような\(U\)を使う時、\(W_1\)と\(W_0\)は、 \begin{align} W_0 &= \frac{1}{\sqrt{|\alpha|^4 + |\beta|^4}}\left(|\alpha|^2 + |\beta|^2U\right)\\ W_1 &= -\frac{\alpha\beta}{|\alpha||\beta|}\frac{1}{\sqrt{2}}\left(I - U\right) \end{align} と簡単になります。

さらに、\(U=iX\)や\(U=iY\)としてみると面白いことがおきます。上の式の\(W_0,W_1\)は一般にはユニタリー演算子では無いのですが、このときだけはユニタリーになるのです。そのことを示すには、x軸回転やy軸回転が、 \[R_x(\theta) = \exp(i\theta X/2)\] と表されていたことと、Pauli行列の性質から \[\exp(i\theta X/2) = \cos\frac{\theta}{2} I + i\sin\frac{\theta}{2} X\] となることを使います。

使うのはこの2つだけなので、\(W_1, W_0\)がユニタリーとなるような\(U\)としては、もちろんPauli行列の3成分 X, Y, Z と三次元の単位ベクトルの内積をとったやつでも構いません。

\(U=iX\)とすると、これらの性質から、\(W_0,W_1\)がどちらとも、以下のようなx軸回転のゲートとなることがわかると思います。 \begin{align} W_0 &= R_x\left(\tan^{-1}\left|\frac{\beta}{\alpha}\right|^2\right)\\ W_1 &= -\frac{\alpha\beta}{|\alpha||\beta|} R_x\left(-\frac{\pi}{2}\right) \end{align} \(\alpha,\beta\)はもともと任意のユニタリー\(V\)の成分を表すものでした。そこで簡単のため\(V\)としてy軸回転を取ることにして、\(\alpha = \cos x, \beta = \sin x\)としてみましょう。そうすると、特に\(W_0\)は、 \[W_0 = R_x\left(\tan^{-1}\tan^2 x\right)\] となります。もともと\(V\)に対して線形に入れたはずの回転角度\(x\)が、観測後は\(\tan^{-1}\tan^2 x\)という妙な関数を通って現れるのです。結構面白い観測の使い方だと思います。実はここで現れた関数\(\sigma(x) = \tan^{-1}\tan^2 x\)はシグモイド関数のような形をしていて、そのことを指して Quantum Neuron と呼んでいるようです。もう一つ面白いのは、\(W_1\)が\(V\)によらずいつも\(R_x\left(-\frac{\pi}{2}\right)\)となること。もし観測して\(\ket{1}\)が出てしまっても、すぐに逆のゲート\(R_x\left(\frac{\pi}{2}\right)\)を掛けてやれば元に戻すことができます。

物理とか

Index