線形回帰分析・最小二乗法とは 共分散・相関係数の意味
1.最小二乗法
実験などによって得られた値が、理論的には線形な関係\(y=ax+b\)を持っていると考えられるとき、得られた実験値からその直線を求めるという作業は、理系なら誰でも経験することだろう。しかし、だいたいの人はExcelかなにかにデータを打ち込み、グラフを書いて、「直線近似」というあらかじめ組み入れられたボタンか何かをクリックして、それで終わりだ。でも、そういう機能を使うにしても、その直線の方程式を求めるのにどういう計算をしているのかは知っている必要があると思うのだ。そこで、今回はそのへんのことについて書いて見ようと思う。
ある適当な確率変数\(X,Y\)から得られたN個の実現値\(x_i,y_i\)があるとする。そして、その間には \[Y=aX+b\tag{1}\] という線形な関係があると仮定しよう。このとき、この仮定からの誤差 \[e_i=ax_i+b-y_i\tag{2}\] という量が最小になるような\(a,b\)が見つかれば、それが実際の値だと考えるのが妥当だろう。しかし、一つだけを考えていてもしょうがないから、この誤差の全体にわたる二乗の和 \[\sum_i e_i^2=\sum_i (ax_i+b-y_i)^2\tag{3}\] を最小にしよう。二乗するのは、±で打ち消して消えてしまわないようにするためだ。もちろん絶対値にしたり4乗にしたりでもいいんだけども、計算がめんどくさいからそういうことはしないのだ。(本当は2乗で計算すると、計算が比較的カンタンというそれ以外にも、とってもいいことがあるけどね。)
じゃあ具体的に(3)を最小にする\(a,b\)を求めてみよう。 \[\sum_i e_i^2=\sum_i (a^2x_i^2+b^2+y_i^2+2abx_i-2ax_iy_i-2by_i)\tag{4}\] となるんだが、これは\(a,b\)を変数とする二次関数とみることができるだろう。そこで、ここからは、 \[f(a,b)=\sum_i e_i^2\tag{5}\] と書くことにする。2変数の二次関数だと少しむずかしい気がしてしまうが、1変数の場合と同じ手順で最小値を求められる。平方完成みたいなことをしてもいいんだが、今回はそれよりも簡単な、微分を使うやり方でやってみることにする。
二次関数の最小値は、その微分が0になる点で求められる。2変数の場合には、偏微分を使って、 \begin{align} \frac{\partial f}{\partial a} &= 0 \\ \frac{\partial f}{\partial b} &= 0 \end{align} を満たすa,bを求めればいい。実際に計算してみよう。 \begin{align} \frac{\partial f}{\partial a} &=\sum_i (2ax_i^2+2bx_i-2x_iy_i)\\ \frac{\partial f}{\partial b} &=\sum_i (2b+2ax_i-2y_i) \end{align} つまり、 \begin{align} \sum_i (2ax_i^2+2bx_i-2x_iy_i) &= 0 \\ \sum_i (2b+2ax_i-y_i) &= 0 \end{align} というa,bに関する連立方程式を得る。
このままだと見た目が難しいので、少し簡単にしてから計算しよう。a,bは和に関係していないので、シグマの外に出せるから、 \begin{align} 2a\sum_ix_i^2+2b\sum_ix_i-2\sum_ix_iy_i &= 0 \\ 2Nb+2a\sum_ix_i-2\sum_iy_i &= 0 \tag{6} \end{align} となる。\(N\)というのはデータの個数だった。みればわかるように、\(\sum_ix_i^2\)とかは、a,bの係数になっているのだ。そこで、\(x_i\)や\(y_i\)の平均や分散・共分散を使って、この係数を書き直してやろう。
まず平均\(\mu_x,\mu_y\)は \[\mu_x=\frac{1}{N}\sum_ix_i\tag{7}\] 分散は \[v_x=\frac{1}{N}\sum_i(x_i-\mu_x)^2=\frac{1}{N}\sum_ix_i^2-\mu_x^2\tag{8}\] 共分散は \[v_{xy}=\frac{1}{N}\sum_i(x_i-\mu_x)(y_i-\mu_y)=\frac{1}{N}\sum_ix_iy_i-\mu_x\mu_y\tag{9}\] と定義されているから、さっきの連立方程式は、 \begin{align} 2a(v_x+\mu_x^2)+2b\mu_x-2(v_{xy}+\mu_x\mu_y) &= 0 \\ 2b+2a\mu_x-2\mu_y &= 0 \tag{7} \end{align} となる。かなり簡単にまとまったから、これを解いてみる。二本目の式に\(\mu_x\)を掛けて \begin{align} 2a(v_x+\mu_x^2)+2b\mu_x &= 2(v_{xy}+\mu_x\mu_y) \\ 2a\mu_x^2+2b\mu_x &= 2\mu_x\mu_y \end{align} としてから、引き算して、 \begin{align} a(v_x+\mu_x^2)-a\mu_x^2&=v_{xy}\\ a&=\frac{v_{xy}}{v_x}\tag{8} \end{align} さらにbを求めると、 \[b=-a\mu_x+\mu_y = \mu_y-\frac{v_{xy}}{v_x}\mu_x \tag{9}\] となる。よって与えられたデータ点\(x_i,y_i\)に対して\(y=ax+b\)という形の線形回帰で、誤差の二乗和\(\sum_i e_i^2=\sum_i (ax_i+b-y_i)^2\)を最小とするものは \[y=\frac{v_{xy}}{v_x}x+\mu_y-\frac{v_{xy}}{v_x}\mu_x\tag{10}\] であることがわかった。
2.共分散と相関係数
(10)で直線近似を(誤差の二乗和が最小となるという意味で)求めることができたが、(10)のままだとよくわからないから、もう少しxとyについて対称的な式に直してみようかと思う。 \begin{align} y&=\frac{v_{xy}}{v_x}x+\mu_y-\frac{v_{xy}}{v_x}\mu_x \\ y-\mu_y &= \frac{v_{xy}}{v_x} (x-\mu_x)\\\\ \frac{y-\mu_y}{\sqrt{v_y}}&=\frac{v_{xy}}{\sqrt{v_y}\sqrt{v_x}} \frac{x-\mu_x}{\sqrt{v_x}}\tag{11} \end{align} わざわざ\(\sqrt{v_y}\)で割ってまでこんな形に持っていったのには大事な意味がある。\(x-\mu_x\)や\(y-\mu_y\)は平均値からの誤差を示す量であり、\(\sqrt{v_x}\)や\(\sqrt{v_y}\)はそういう誤差(ばらつき)の代表的な大きさを示す量だった。つまり、 \[x_{norm}=\frac{x-\mu_x}{\sqrt{v_x}}, y_{norm}=\frac{y-\mu_y}{\sqrt{v_y}}\tag{12}\] とでも定義してやると、\(x_{norm},y_{norm}\)というのは\(x,y\)が統計的に規格化されたような量になる。計算してみれば簡単にわかるが、\(x_{norm},y_{norm}\)の平均は0だし、分散は1になる。
例として、以下のような散布図を考えてみよう。
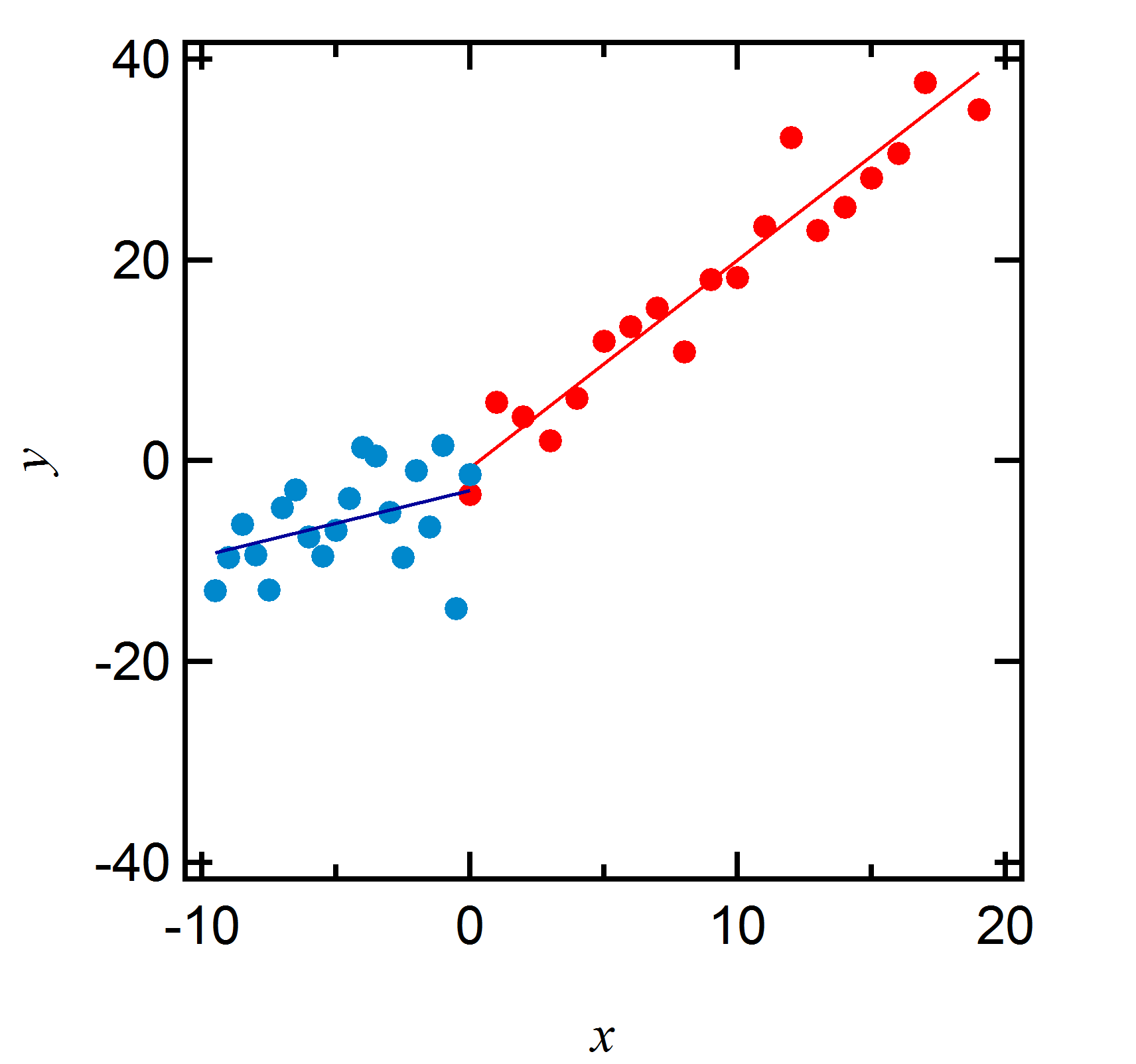
2つの系列のデータとそれに対する線形回帰直線を書いてみた。このままだとどちらのほうが相関があって、どちらのほうが無いのか、ということが視覚的にはわかりにくい。そこで(12)式のように規格化を行ってみると、
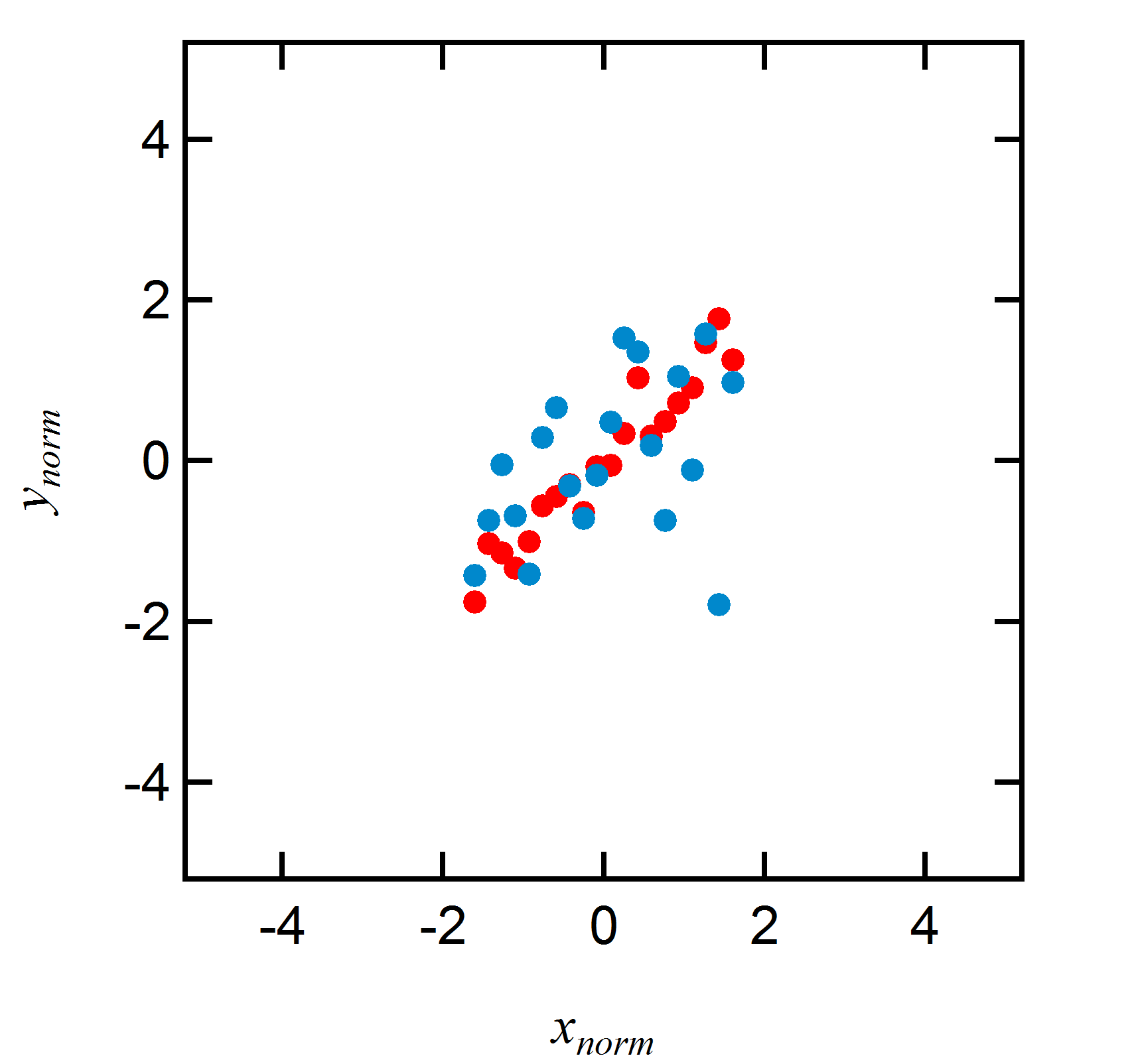
そこでそういう比例関係の強さを示す量として、(11)式で\(x_{norm},y_{norm}\)を結びつける比例定数 \[R=\frac{v_{xy}}{\sqrt{v_y}\sqrt{v_x}}\tag{13}\] を
相関係数
という。 ちなみにさっきのグラフでは、赤がR=0.96, 青がR=0.40となっている。こういうふうに、相関係数というのは比例関係の強さをわかりやすく表現しているのだ。これで、共分散というのも意味が少しは分かってくるんじゃないかと思う。