情報量とエントロピー - 導出と性質
1. 情報量
私達が「情報」と聞いて思い浮かべるものは様々です。例えば、今日の天気だとか、料理のレシピ、さらには誰々が誰々と付き合っているなんてものも、全て「情報」でしょう。では、それぞれの情報について、「情報の大きさ」=「情報量」とはどのように定義すればよいでしょうか?そこで天気を例にして、どんな情報が大きな情報を持っているか考えてみましょう。
- 今日のサハラ砂漠は晴れだった。
- 今日のサハラ砂漠は雨だった。
なぜ「砂漠で雨が降った」という情報が人に驚きを与えるのでしょうか?それは、その出来事があまり起こりそうもないことだからです。逆に「砂漠で晴れた」という情報はほとんど驚きを与えませんが、これはその出来事が頻繁に起こっていることだからです。
このように考えると、ある出来事が起こる「確率」が情報量に結びついていそうです。確率が小さいものほど情報量は大きく、確率が大きいものほど情報量は小さいわけです。そこで、このことを数式に書き表してみます。確率\(p\)で起こる出来事と、確率\(p'\)で起こる出来事がもつ情報量をそれぞれ\(I(p),I(p')\)とします。このとき、 \[p\gt p' \Rightarrow I(p) \lt I(p) \tag{1}\] が成り立つはずです。
確率が情報量と密接に結びついていることがわかったところで、次に、2つの情報が入ってきたときの情報量について考えてみましょう。2つの情報が全く独立に送られてきたとき、全体の情報量は、直感的にその2つの情報量の足し算になるべきですよね。このことも数式にしてしまいます。2つの独立な情報の起こる確率を\(p_1,p_2\)とすると、同時に起こる確率はそれらの掛け算で\(p_1p_2\)です。したがって、先に定義した情報量\(I(p)\)を使って、この2つの情報を合わせた情報量は\(I(p_1p_2)\)と表せます。その一方で、\(p_1,p_2\)の情報それぞれが持つ情報量は\(I(p_1),I(p_2)\)ですから、次が成り立つべきだといえます。 \[I(p_1p_2) = I(p_1) + I(p_2)\tag{2}\] さて、(1),(2)式が満たされるような関数はどんなものがあるでしょうか?特に(2)の性質が情報量を特徴づけているわけですが、これは
対数関数
の性質そのものです。(高校数学を思い出してください。\(\log ab = \log a + \log b\)でしたね。) そこで適当な定数\(a\)を底として、\(I(p) =\log_a p\)としてみましょう。(2)の性質はどんな\(a\)に対しても成り立ちますから、計算を簡単にするために\(a\)は\(1\)以上ということにしておきます。でもそうすると、確率が小さくなるほど情報量は多くなる、という(1)の性質が満たされなくなってしまいますが、これは最初に\(-\)をつければ解決できます。このような考えによって、確率\(p\)で起こる情報の「情報量」を次で定義します。 \[I(p) = -\log_a p\] 適当な定数\(a\)の分だけ任意性が残っていますが、情報理論では通常\(a=2\)として \[I(p) = -\log_2 p\tag{3}\] とします。情報量は無次元の (m, kgのような単位の無い) 量ですが、慣例的に\(a=2\)とした情報量の単位は"bit"が使われます。情報理論の文脈では、\(2\)を省略してしまって、 \[I(p) = -\log p\] と書かれることも多いです。このページでもこの記法を採用します。
なぜ底として\(2\)を使うのでしょうか?それを真に理解するには、符号化の話を知らないといけませんが、簡単な説明をしてみます。例えば確率\(1/4\)で起こる4つの情報があったとしましょう。それぞれの情報量は\(-\log_2 1/4 = 2\) (bit) です。一方でコンピュータでこの情報を送るときのことを考えてみましょう。\(1,0\)の2つの値だけを使って、4つの情報を区別するには、\(00,01,10,11\)の4通りの bit 列を使えば良さそうです。するとどうでしょう?底を\(2\)としたときの情報量 (= 2 bit) と1つの情報を送るために必要なbitの長さ (= 2 bit)が一致しています。一般に、底を\(2\)とすることによって、ある情報の情報量と、その情報を送るために必要な bit の長さとがほぼ一致するのです。
2.平均情報量・エントロピー
次に平均情報量を定義します。\(n\)個の情報が、確率\(p_1,...,p_n\)で起こるとしましょう。このとき、この情報源\(X\)から得られる平均的な情報量は、以下で計算できますね。 \[H(X) = -\sum_{i=1}^n p_i\log p_i\tag{4}\] この量\(H(X)\)はエントロピー
とも呼ばれます。3.結合エントロピー
2つの情報源\(X,Y\)があって、その2つから同時に\((x,y)\)という情報が得られる確率を\(p(x,y)\)とします。\((x,y)\)という組を1つの情報であると考えれば、その平均情報量は上と全く同じように計算できますね。つまり \[H(X,Y) = \sum_{x,y} p(x,y)\log p(x,y)\tag{5}\] が情報源\(X,Y\)を1つの情報源とみなしたときの平均情報量です。(5)式は、2つの情報現を1つに「つなげて」考えたエントロピーなので、これは結合エントロピー
と呼ばれます。ところで、結合エントロピーは、\(X\)の平均情報量\(H(X)\)と\(Y\)の平均情報量\(H(Y)\)の、単純な和になるでしょうか?結合エントロピーは、2つの情報源をあわせたものから得られる平均情報量なわけですから、なんとなくそうなっていそうな気がします。しかしながら、このことは\(X\)と\(Y\)が独立であるときにしか成り立ちません。\(X,Y\)が独立でないということはつまり、\(X\)からある情報\(x_0\)を得たときに\(Y\)からある\(y_0\)を得る確率が、独立に\(y_0\)を得る確率\(p(y_0)\)よりも、高かったり低かったりするということです。このようなときには、\(X\)の情報から少なからず\(Y\)の情報を得ることができてしまいます。だから単純な和にはならないのです。
独立であるときには\(H(X,Y)=H(X)+H(Y)\)が成り立つことを、一応数式で示しておきましょう。\(X,Y\)が独立であるということは、\(p(x,y) = p(x)p(y)\)が成り立つということですから、(5)に代入してやります。 \begin{align} H(X,Y) &= -\sum_{x,y} p(x,y)\log p(x,y) \\ &= -\sum_{x,y} p(x)p(y)\log p(x)p(y) \\ &= -\sum_{x,y} p(x)p(y)(\log p(x) + \log p(y)) \\ &= -\sum_{x,y} p(x)p(y)\log p(x) - \sum_{x,y} p(x)p(y)\log p(y) \\ &= -\sum_y p(y)\sum_{x} p(x)\log p(x) - \sum_x p(x)\sum_{y} p(y)\log p(y) \end{align} 最後に\(\sum_x p(x) = \sum_y p(y) = 1\)に注意すると、 \begin{align} H(X,Y) &= -\sum_{x} p(x)\log p(x) - \sum_{y} p(y)\log p(y) \\ &= H(X) + H(Y) \end{align} を得ます。
情報源\(X,Y\)が独立であるとき、\(H(X,Y)=H(X)+H(Y)\)が成り立ちます。
4.相互情報量
\(X,Y\)が独立でないときには一般に\(H(X,Y)=H(X)+H(Y)\)は成り立ちません。この原因は何かと考えると、それはある意味で\(X,Y\)の情報の間に「重なり」があることです。この「重なり」を相互情報量 \(I(X,Y)\)
と呼びます。\(X,Y\)が与える情報の間に、下図に示すような重なりがあると考えてみましょう。先程見たように、全体の平均情報量は結合エントロピーは\(H(X,Y)\)であると考えられます。各々の平均情報量は\(H(X)\), \(H(Y)\)で、それぞれ図のピンク色と水色の部分に相当します。図に基づいて考えると、 \[H(X,Y) = H(X) + H(Y) - I(X,Y)\tag{6}\] が成り立っていそうですから、少し変形して、 \[I(X,Y) = H(X) + H(Y) - H(X,Y)\tag{7}\] を相互情報量の定義とします。これで2つの情報源\(X,Y\)の「重なり」を定式化することができました。
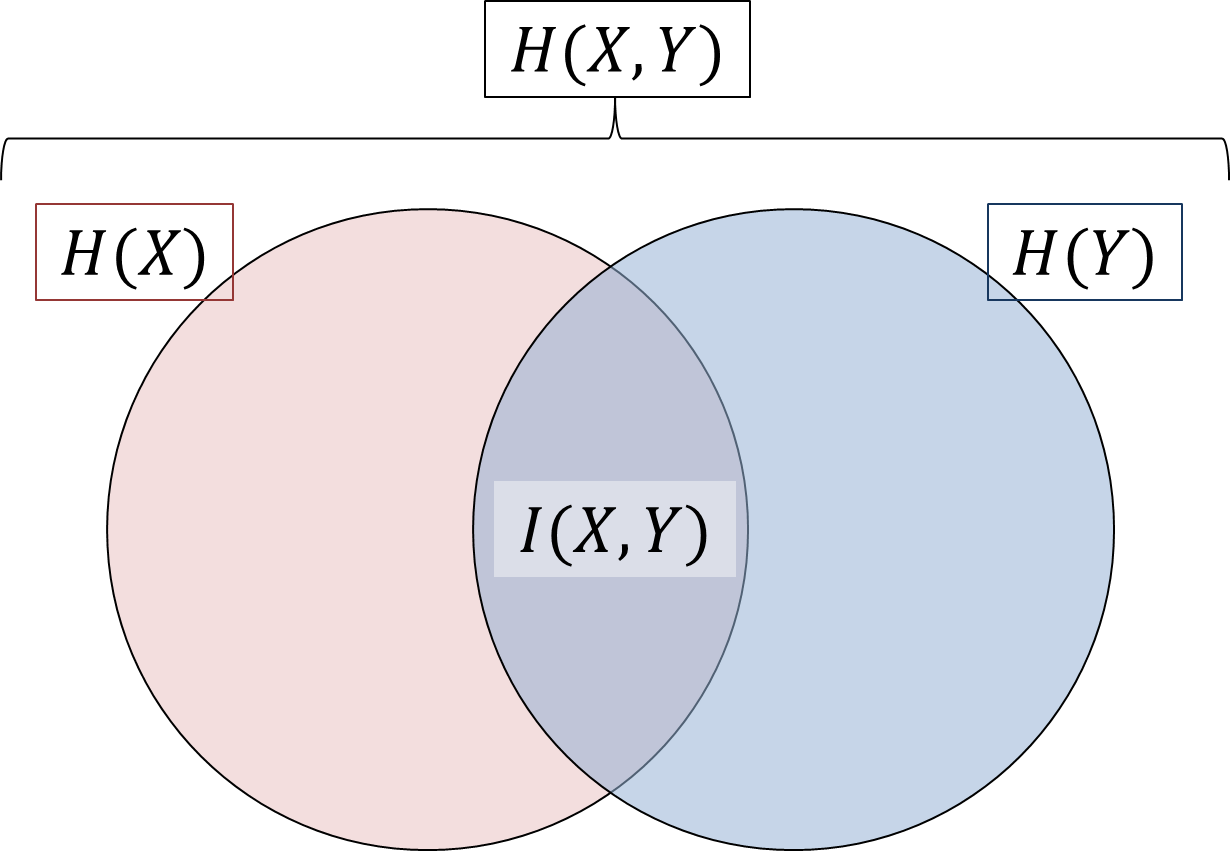
情報源\(X,Y\)が独立であるとき、\(I(X,Y)=0\)が成り立ちます。
5.条件付きエントロピー
\(X,Y\)の重なりを定式化すると、それ以外の部分も定式化しておきたい、と思うのはとても自然ですね。先程の図では数式が抜けていた部分を、条件付きエントロピー \(H(X|Y), H(Y|X)\)
と呼びます。これですっきりと図の領域をまとめることができました。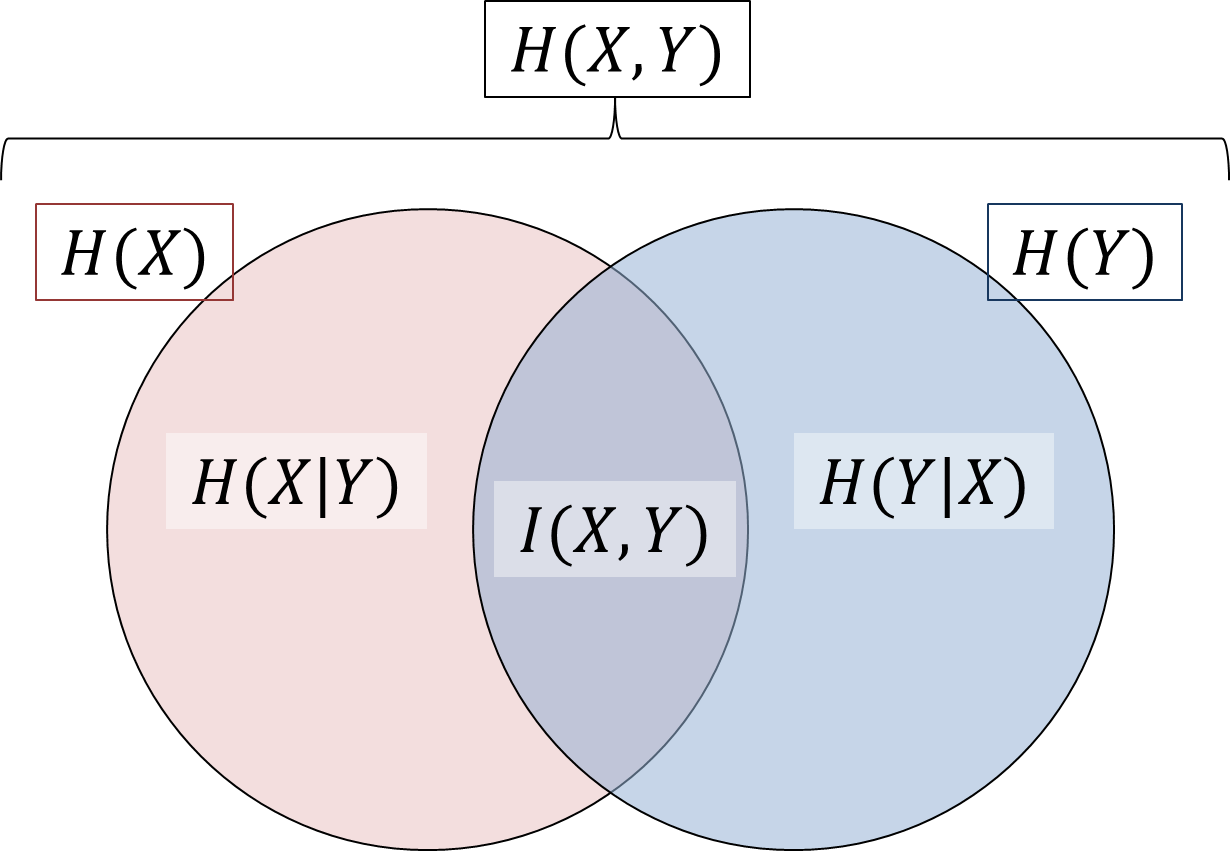
図から、 \begin{align} H(X|Y) &= H(X) - I(X,Y)\\ &= H(X,Y) - H(Y) \end{align} と計算すれば良いことがわかります。\(H(X,Y) = -\sum_{x,y} p(x,y)\log p(x,y)\) や \(H(Y) = -\sum_y p(y)\log p(y)\)を代入すると、 \begin{align} H(X|Y) &= -\sum_{x,y} p(x,y)\log p(x,y) + \sum_y p(y)\log p(y) \\ &= -\sum_y \left(\sum_x p(x,y)\log p(x,y) - p(y)\log p(y)\right) \end{align} となります。条件付きエントロピーという名前からも予想がつくかもしれませんが、ここで条件付き確率\(p(x|y)\)を導入します。条件付き確率\(p(x|y)\)とは、情報源\(Y\)からある情報\(y\)を得たという条件の下で、情報源\(X\)から\(x\)という情報を得る確率です。数式では\(p(x,y) = p(y)p(x|y)\)と定義されます。
数式だけでなく言葉で言い直してみると、\((x,y)\)という情報を得る確率が、\(y\)を得る確率\(p(y)\)と、\(y\)を得た上で\(x\)を得る確率\(p(x|y)\)の積になるという定義です。直感をそのまま式にした感じですね。
この条件付き確率を使うと、 \begin{align} H(X|Y) &= -\sum_y \left(\sum_x p(y)p(x|y)\log p(y)p(x|y) - p(y)\log p(y)\right)\\ &= -\sum_y p(y)\left(\sum_x p(x|y)\log p(y)p(x|y) - \log p(y)\right)\\ &= -\sum_y p(y)\left(\sum_x p(x|y)\log p(x|y) + \sum_x p(x|y)\log p(y) - \log p(y)\right) \end{align} ここで条件付き確率といえども、全ての場合を足し合わせると\(\sum_x p(x|y) = 1\)が成り立つことに注意します。これを使えば、条件付きエントロピーの計算式として \[H(X|Y) = -\sum_y p(y) \left(\sum_x p(x|y)\log p(x|y)\right) \tag{8}\] を得ます。このままだとかなり複雑で意味がわかりにくいので、この数式を噛み砕いてみましょう。まず括弧の中身 \(\sum_x p(x|y)\log p(x|y)\) は \(y\) という情報を得たという条件の下で、\(X\)からさらに得られる平均情報量を表している、と考えられます。記号を使って書くとするなら\(H(X|Y=y)\)というところでしょうか。(あまりこういう書き方は見たこと無い気もしますが、説明のために使います。) そうすると、条件付きエントロピーは \[H(X|Y) = \sum_y p(y) H(X|Y=y)\] となっていて、それぞれの\(y\)について\(X\)に「残る」情報量を、さらに平均化したものであると解釈できますね。そんなふうに考えると、\(H(X|Y)\)という量は、情報源\(Y\)からの情報を「条件」としたときの、\(X\)の平均的なエントロピーを表しているいて、確かに「条件付き」エントロピーという呼び方が理にかなっていると納得できると思います。さて最後に、結合エントロピーに関して、直感的には当然と思われる性質を1つ示して終わりにしたいと思います。条件付きエントロピーを使えば、結合エントロピーは \[H(X,Y) = H(X) + H(Y|X)\] と書くことができます。(8)式をみると\(p(y|x)\lt 1\)であることから、\(H(Y|X)\)は常に正であることがわかります。よって、次がいえます。
\(H(X,Y) \geq H(X)\), つまり\(X\)と\(Y\)をあわせた系のエントロピーは、\(X\)のエントロピーよりも必ず大きくなります。
実は量子力学において情報を考えると、この性質が破れていることが示されます。不思議ですね。