ポテンシャルの近似展開とルジャンドル多項式
多項式に関することだし、微分方程式のページに入れるかどうか迷ったけれど、ルジャンドル多項式が微分方程式で大事な関数だからここに入れることにした。
展開がうまくいく方法としては、\(y=2ax-x^2\)とおいて、 \[g(y)=\frac{1}{\sqrt{1-y}}\] のテイラー展開を利用するものがあるから、それを今回は使ってみよう。g(y)のn階微分はすぐに求めることができる。 \[\frac{d^n g}{dy^n}=\frac{1\cdot3\cdot5\cdots(2n-1)}{2^n}(1-y)^{-\frac{1}{2}-n}\] だからg(y)はつぎのように展開される。 \[g(y)=\sum_{n=0}^\infty\frac{(2n-1)!!}{2^n n!}y^n\] ただしこのページでは\((-1)!!=1\)ということにしておこう。\(y=2ax-x^2\)としたから、これを戻してやると、 \[f(x)=\sum_{n=0}^\infty\frac{(2n-1)!!}{2^n n!}(2a-x)^nx^n\] さらに二項定理から、 \[(2a-x)^n = \sum_{k=0}^n \frac{n!}{k!(n-k)!} (2a)^k(-x)^{n-k}\] だから、 \begin{align} f(x)&=\sum_{n=0}^\infty\frac{(2n-1)!!}{2^n n!}x^n\left(\sum_{k=0}^n \frac{n!}{k!(n-k)!} (2a)^k(-x)^{n-k}\right)\\ &=\sum_{n=0}^\infty\sum_{k=0}^n\frac{(2n-1)!!}{2^{n-k} k!(n-k)!}(-1)^{n-k}a^k x^{2n-k}\tag{3} \end{align} である。目指す形は(2)のような形なんだが、まだまだ遠い。そこでまずはパラメータの変換をしてみる。xの肩に乗っている数字をひとまとめにして\(p=2n-k\)として、ついでにたくさん出てきている\(n-k\)も\(q=n-k\)としてまとめてやろう。
パラメータを変換するときは、和を取る範囲についてしっかりと考えないといけない。いま(3)式で和を取っている範囲というのは、 \[0\leq n,~~0\leq k\leq n\] である。\(n,k\)は\(p,q\)によって表すと\(n=p-q\), \(k=p-2q\)だから、上の不等式は、 \[0\leq p-q,~~0\leq p-2q\leq p-q\] となり、したがって、 \[q\leq p,~~2q\leq p\leq p+q\] が和を取る範囲となる。二番目のやつをわけて書くと、 \[q\leq p,2q\leq p,p\leq p+q\] つまり、 \[q\leq p,q\leq p/2,0\leq q\] である。一番目の式は二番目の式が成り立っていれば勝手にOKになるから、結局、 \[0\leq q, q\leq p/2\] が和をとる範囲となる。この範囲は、pqのグラフを書いてみればわかるが、 \[0\leq p, 0\leq q\leq p/2\] と同じことである。
範囲についてしっかり考えたところで、もとの問題に戻ろう。上の考察から、パラメータを\(p,q\)に変換したとき、 \[f(x)=\sum_{p=0}^\infty\sum_{q=0}^{\lfloor \frac{p}{2}\rfloor}\frac{(2p-2q-1)!!}{2^q (p-2q)!q!}(-1)^qa^{p-2q} x^p\] となる。わかりにくいが、これで\(f(x)=\sum_pc_px^p\)の形を作れているので、当初の目的を達成することができているのだ。具体的な係数\(c_n\)の形としては、 \[c_p=\sum_{q=0}^{\lfloor \frac{p}{2}\rfloor}\frac{(2p-2q-1)!!}{2^q (p-2q)!q!}(-1)^q a^{p-2q}\] である。二重階乗が入っているのが気持ち悪いので、 \[(2n-1)!!=\frac{(2n)!}{2^nn!}\] という公式を使って書き直してやると、(n=0のときにも(-1)!!=1としたから成り立っている) \[c_p=\sum_{q=0}^{\lfloor \frac{p}{2}\rfloor}\frac{(2p-2q)!}{2^p q!(p-q)!(p-2q)!}(-1)^q a^{p-2q}\] となる。
ということで、これがクーロンポテンシャルや万有引力ポテンシャルを近似展開したときの係数である。この係数はaを変数とみたとき
1.ポテンシャルの近似展開
万有引力やクーロン力のポテンシャルエネルギーは、物体間の距離に反比例して、 \[\phi(|\b{r}-\b{r}'|) = \frac{A}{|\b{r}-\b{r}'|}\tag{1}\] の形で与えられる。よく問題となるものとして、下の図のように、クーロン力や引力を作る物質が原点まわりに存在していて、そこから遠く離れた\(\b{r}\)の点でのポテンシャルを知りたいというのがある。今回はこういう状況で、(1)式を近似展開する方法についてやってみようと思う。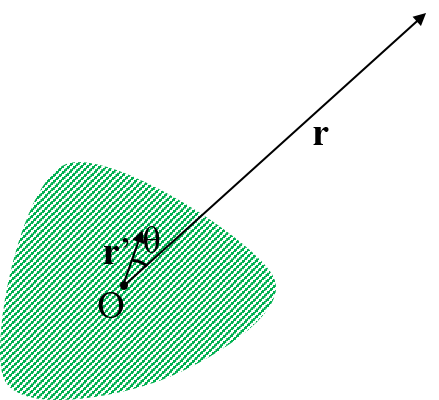
2.計算
はじめこの\(f(x)\)を展開しようとして、 \[f(x)=\sum_{n=0}^\infty \frac{1}{n!}f^{(n)}(0)x^n\tag{2}\] しようとしたが、うまくいかない。そもそも、\(f(x)\)のn階微分を一般式で見つけることができなかったのだ。展開がうまくいく方法としては、\(y=2ax-x^2\)とおいて、 \[g(y)=\frac{1}{\sqrt{1-y}}\] のテイラー展開を利用するものがあるから、それを今回は使ってみよう。g(y)のn階微分はすぐに求めることができる。 \[\frac{d^n g}{dy^n}=\frac{1\cdot3\cdot5\cdots(2n-1)}{2^n}(1-y)^{-\frac{1}{2}-n}\] だからg(y)はつぎのように展開される。 \[g(y)=\sum_{n=0}^\infty\frac{(2n-1)!!}{2^n n!}y^n\] ただしこのページでは\((-1)!!=1\)ということにしておこう。\(y=2ax-x^2\)としたから、これを戻してやると、 \[f(x)=\sum_{n=0}^\infty\frac{(2n-1)!!}{2^n n!}(2a-x)^nx^n\] さらに二項定理から、 \[(2a-x)^n = \sum_{k=0}^n \frac{n!}{k!(n-k)!} (2a)^k(-x)^{n-k}\] だから、 \begin{align} f(x)&=\sum_{n=0}^\infty\frac{(2n-1)!!}{2^n n!}x^n\left(\sum_{k=0}^n \frac{n!}{k!(n-k)!} (2a)^k(-x)^{n-k}\right)\\ &=\sum_{n=0}^\infty\sum_{k=0}^n\frac{(2n-1)!!}{2^{n-k} k!(n-k)!}(-1)^{n-k}a^k x^{2n-k}\tag{3} \end{align} である。目指す形は(2)のような形なんだが、まだまだ遠い。そこでまずはパラメータの変換をしてみる。xの肩に乗っている数字をひとまとめにして\(p=2n-k\)として、ついでにたくさん出てきている\(n-k\)も\(q=n-k\)としてまとめてやろう。
パラメータを変換するときは、和を取る範囲についてしっかりと考えないといけない。いま(3)式で和を取っている範囲というのは、 \[0\leq n,~~0\leq k\leq n\] である。\(n,k\)は\(p,q\)によって表すと\(n=p-q\), \(k=p-2q\)だから、上の不等式は、 \[0\leq p-q,~~0\leq p-2q\leq p-q\] となり、したがって、 \[q\leq p,~~2q\leq p\leq p+q\] が和を取る範囲となる。二番目のやつをわけて書くと、 \[q\leq p,2q\leq p,p\leq p+q\] つまり、 \[q\leq p,q\leq p/2,0\leq q\] である。一番目の式は二番目の式が成り立っていれば勝手にOKになるから、結局、 \[0\leq q, q\leq p/2\] が和をとる範囲となる。この範囲は、pqのグラフを書いてみればわかるが、 \[0\leq p, 0\leq q\leq p/2\] と同じことである。
範囲についてしっかり考えたところで、もとの問題に戻ろう。上の考察から、パラメータを\(p,q\)に変換したとき、 \[f(x)=\sum_{p=0}^\infty\sum_{q=0}^{\lfloor \frac{p}{2}\rfloor}\frac{(2p-2q-1)!!}{2^q (p-2q)!q!}(-1)^qa^{p-2q} x^p\] となる。わかりにくいが、これで\(f(x)=\sum_pc_px^p\)の形を作れているので、当初の目的を達成することができているのだ。具体的な係数\(c_n\)の形としては、 \[c_p=\sum_{q=0}^{\lfloor \frac{p}{2}\rfloor}\frac{(2p-2q-1)!!}{2^q (p-2q)!q!}(-1)^q a^{p-2q}\] である。二重階乗が入っているのが気持ち悪いので、 \[(2n-1)!!=\frac{(2n)!}{2^nn!}\] という公式を使って書き直してやると、(n=0のときにも(-1)!!=1としたから成り立っている) \[c_p=\sum_{q=0}^{\lfloor \frac{p}{2}\rfloor}\frac{(2p-2q)!}{2^p q!(p-q)!(p-2q)!}(-1)^q a^{p-2q}\] となる。
ということで、これがクーロンポテンシャルや万有引力ポテンシャルを近似展開したときの係数である。この係数はaを変数とみたとき