量子ゲートテレポーテーション
1. 最大にエンタングルした状態への局所ゲート
最大エンタングル状態の記事でも解説したように、量子系 A, B にまたがる最大エンタングル状態 \begin{align} \ket{\psi^{AB}} = \frac{1}{\sqrt{N}} \sum_{i=1}^N \ket{i}_A\ket{i}_B \end{align} (ただし \(\ket{i}_A, \ket{i}_B\) はそれぞれ A, B の正規直交基底) に対する局所操作 (I \otimes U) は次のように、作用させたのがどちらかわからない、という性質を持っていた。 \begin{align} (I \otimes U) \ket{\psi^{AB}} &= (U^T \otimes I) \ket{\psi^{AB}} \\ \frac{1}{\sqrt{N}} \sum_{i=1}^N \ket{i}_A\left(U\ket{i}_B\right) &= \frac{1}{\sqrt{N}} \sum_{i=1}^N \left(U^T \ket{i}_A\right)\ket{i}_B \end{align} この性質に着目したテクニックが、ゲートテレポーテーションである。2. 最大エンタングル状態でのゲートテレポーテーション
ここでは簡単のため2つの量子ビットを使って考えよう。量子ビットA、Bにまたがる最大エンタングル状態 \(\frac{1}{\sqrt{2}} \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right)\) を用意し、A にユニタリー \(U\) を作用させると \begin{align} (U \otimes I) \ket{\psi^{AB}} &= \frac{1}{\sqrt{2}} \left[(U\ket{0}_A)\ket{0}_B + (U\ket{1}_A)\ket{1}_B\right] \\ &= \frac{1}{\sqrt{2}} \left[\ket{0}_A(U^T\ket{0}_B) + \ket{1}_A(U^T\ket{1}_B)\right] \end{align} が得られる。Aの状態を \(\{\ket{0}, \ket{1}\}\) 基底で射影測定すると、その結果によって状態が変化する。\(\ket{0}\) が測定されたとき、状態は \begin{align} \to \ket{0}_A (U^T\ket{0}_B) \end{align} へと収束し、\(\ket{1}\) が観測されたときには \begin{align} \to \ket{1}_A (U^T\ket{1}_B) \end{align} へと収束する。(エンタングル状態をつくるためのゲートも含めて) 図にすると以下のようになる。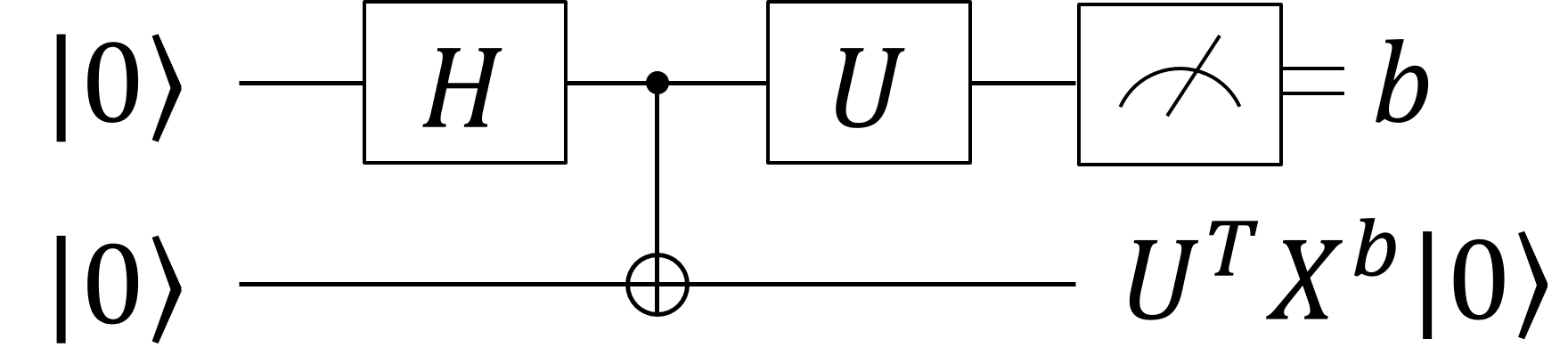
さて、今 \(\frac{1}{\sqrt{2}} \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right)\) を用意した場合を考えたが、最初に用意するエンタングル状態を \(\frac{1}{\sqrt{2}} \left(\ket{0}_A\ket{0}_B + \ket{1}_A\ket{1}_B\right)\) から \(\frac{1}{\sqrt{2}} \left(\ket{0}_A\ket{0}_B - \ket{1}_A\ket{1}_B\right)\) へと変えたとしても、どちらも最大にエンタングルした状態には変わりないのだから、同様のことができるはずである。そこでこの場合についても計算してみよう。 この現象を一般化させたものがゲートテレポーテーションと呼ばれる手法である。
3. ゲートテレポーテーション
初期状態の片割れを、\(\ket{0}_A\) から任意の状態 \(\ket{\psi}_A = \alpha \ket{0} + \beta \ket{1}\) へと変えてやっても、実は同様の現象が起こる。以下の図のような操作を考えよう。